![REPTE:
Construir caixes per envasar
croissants cúbics
innovar
v. tr. [LC] Introduir quelcom de nou (en una cosa)
Dissenyar un envàs que contingui el
màxim nombre de croissants cúbics
utilitzant el mínim de material, i, els
guiarem per treballar la relació entre
longituds, àrees i volums.
Imatge:https://www.dolcesalato.com/2023/07/17/dalla-svezia-a-it
alia-croissant-a-forma-cubo-che-fa-impazzire-tutti/](https://image.slidesharecdn.com/4-250403090527-5ab87791/85/4-El-crube-el-nou-outfit-del-croissant-Rao-entre-longitud-area-i-volum-1-pdf-4-320.jpg)
4. El crube, el nou outfit del croissant. Raó entre longitud, àrea i volum. (1).pdf
- 1. SECUNDÀRIA GUIES DIDÀCTIQUES Sílvia Salvador Imma Casas EL CRUBE, EL NOU OUTFIT DEL CROISSANT RAÓ ENTRE LONGITUD, ÀREA I VOLUM FLORENCE PER LA MILLORA DE LES MATEMÀTIQUES
- 3. CONTEXT, IDEA I REPTE
- 4. REPTE: Construir caixes per envasar croissants cúbics innovar v. tr. [LC] Introduir quelcom de nou (en una cosa) Dissenyar un envàs que contingui el màxim nombre de croissants cúbics utilitzant el mínim de material, i, els guiarem per treballar la relació entre longituds, àrees i volums. Imatge:https://www.dolcesalato.com/2023/07/17/dalla-svezia-a-it alia-croissant-a-forma-cubo-che-fa-impazzire-tutti/
- 5. Si fóssiu els responsables de dissenyar el millor envàs per aquests croissants, com us l’imagineu? Si féssim una caixa per als croissants normals, creieu que necessitaríem més o menys material que amb els cúbics?
- 6. D’ON VENIM? ● Magnituds ● Longitud ● Àrea ● Volum A ON ANEM? ● Construir figures 3D. Treballar el Volum. ● Representar 3D en 2D i viceversa ● Connectar la relació entre la raó de semblança i les dimensions.
- 7. OBJECTIUS
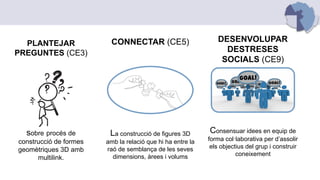
- 8. PLANTEJAR PREGUNTES (CE3) CONNECTAR (CE5) La construcció de figures 3D amb la relació que hi ha entre la raó de semblança de les seves dimensions, àrees i volums DESENVOLUPAR DESTRESES SOCIALS (CE9) Consensuar idees en equip de forma col·laborativa per d’assolir els objectius del grup i construir coneixement sobre procés de construcció de formes geomètriques 3D amb multilink.
- 9. Objectius: Plantejar preguntes sobre el procés de construcció de formes geomètriques 3D, amb material manipulable (multilink), per tal d’integrar les principals estratègies per calcular àrees i volums en diferents situacions i contextos. (CE3) 1r-OBJECTIU D’APRENENTATGE
- 11. Activem coneixements previs Material: Recursos materials i activitats experimentals en l’educació matemàtica a secundària Anton Aubanell Pou
- 12. CONNEXIONS
- 13. Objectius: Connectar la construcció de figures 3D amb la relació que hi ha entre la raó de semblança de les seves dimensions, la raó de les seves àrees i la raó entre els seus volums, per desenvolupar una visió matemàtica com un tot integrat. (CE5) . 2n-OBJECTIU D’APRENENTATGE
- 15. Objectius: Plantejar preguntes sobre el procés de construcció de formes geomètriques 3D, amb diferents eines, per tal d’integrar les principals estratègies per calcular àrees i volums en diferents situacions i contextos. (CE3) 1r-OBJECTIU D’APRENENTATGE Connectar la construcció de figures 3D amb la relació que hi ha entre la raó de semblança de les seves dimensions, la raó de les seves àrees i la raó entre els seus volums, per desenvolupar una visió matemàtica com un tot integrat. (CE5) 2n-OBJECTIU D’APRENENTATGE
- 16. construïm i comptem … "De quina manera col·loquem els croissants per embolicar-los amb el mínim material?"
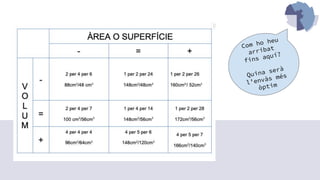
- 17. una mica d’acció EL REPTE és completar el quadre de la dreta amb els ortoedres ordenats, seguint les instruccions següents: d’esquerra a dreta, la superfície de l’àrea de les formes ha de créixer. Anant de dalt a baix, el volum de les formes ha de créixer. Totes les formes de la columna del mig han de tenir la mateixa àrea. Totes les formes de la fila del mig han de tenir el mateix volum. https://nrich.maths.org/problems/ch anging-areas-changing-volumes
- 18. Com ho heu arribat fins aquí? Quina serà l’envàs més òptim
- 19. CONCRETA: Els policubs ICÒNICA: les imatges aBSTRACTA: Els SÍMBOLS
- 20. Objectius: Plantejar preguntes sobre el procés de construcció de formes geomètriques 3D, amb diferents eines, per tal d’integrar les principals estratègies per calcular àrees i volums en diferents situacions i contextos. (CE3) 1r-OBJECTIU D’APRENENTATGE
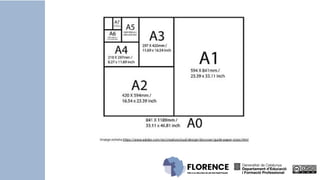
- 22. ens plantegem preguntes Quina és la raó entre les dimensions del full A0 i el full A1 ? Quants A3 necessitem per fer un A0?Quina és la raó entre les seves àrees? Si agafem com unitat de superfície la fulla A1. Quants fulls A2 necessitem per fer un A1? Quants A7? Quants A10? Quants fulls del format A4 necessitem per obtenir un full A0? Quina fracció de A0 és A4? Quin és el paper més gran de la sèrie A? Quines són les seves dimensions en cm? Quant val la seva superficie en cm2 ?
- 24. Objectius: Plantejar preguntes sobre el procés de construcció de formes geomètriques 3D, amb diferents eines, per tal d’integrar les principals estratègies per calcular àrees i volums en diferents situacions i contextos. (CE3) 1r-OBJECTIU D’APRENENTATGE Connectar la construcció de figures 3D amb la relació que hi ha entre la raó de semblança de les seves dimensions, la raó de les seves àrees i la raó entre els seus volums, per desenvolupar una visió matemàtica com un tot integrat. (CE5) 2n-OBJECTIU D’APRENENTATGE
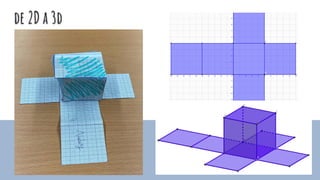
- 25. de 2D a 3d
- 26. Objectius: Desenvolupar destreses socials: col·laborar activament amb els altres per consensuar idees en equip de forma col·laborativa, per tal d’assolir els objectius del grup i construir coneixement conjuntament. (CE9) 3r-OBJECTIU D’APRENENTATGE
- 27. construïm l’envàs REPTE, construir caixes cúbiques per envasar croissants cúbics d’aresta 5 cm.
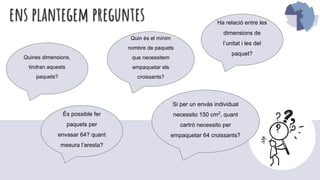
- 28. ens plantegem preguntes Ha relació entre les dimensions de l’unitat i les del paquet? És possible fer paquets per envasar 64? quant mesura l’aresta? Quin és el mínim nombre de paquets que necessitem empaquetar els croissants? Quines dimensions, tindran aquests paquets? Si per un envàs individual necessito 150 cm2 , quant cartró necessito per empaquetar 64 croissants?
- 30. Què m’emporto dels aprenentatges?
- 37. how small can be big
- 38. AVALUEM :)
- 39. avaluació Activitats individuals Fitxes per comprovar l’assoliment dels objectius i criteris d’avaluació. Rubrica Observació a l’aula, Ajustar ritmes i atendre les necessitats de l’alumnat. Feedback al Drive Comentaris en la presentació "Què m’emporto" per fer propostes de millora. Èxit tiquets, Valoració de cada sessió amb diferents opcions a escollir.Èxit tiquets Destreses socials. Corubrics ✔ Autoavaluació ✔ Coavaluació
- 40. com ho podem estirar?
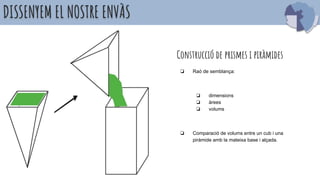
- 41. DISSENYEM EL NOSTRE ENVÀS Construcció de prismes i piràmides ❏ Raó de semblança: ❏ dimensions ❏ àrees ❏ volums ❏ Comparació de volums entre un cub i una piràmide amb la mateixa base i alçada.
- 42. DISSENYEM EL NOSTRE ENVÀS Modelització amb Geogebra ❏ Relació entre perímetre i dimensions d’un rectangle ❏ Tipus de funció ❏ Variació de l’àrea en funció dels costats. ❏ Rectangle d’àrea màxima ❏ Anàlisi ortoedres amb superfície fixa ❏ H ha un volum màxim?
- 43. MOLTES GRÀCIES