Bab 8
Download as DOCX, PDF0 likes388 views
Dokumen ini membahas garis singgung lingkaran, termasuk pengertian, sifat, dan cara menggambarnya. Terdapat penjelasan tentang panjang garis singgung, kedudukan dua lingkaran, serta contoh penerapan garis singgung dalam kehidupan sehari-hari. Di akhir, terdapat soal untuk melatih pemahaman tentang topik yang dibahas.
Bab 8
- 1. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 47 - Bab 8 Garis Singgung Lingkaran 8.1 Mengenal Garis Singgung Lingkaran Penjelasan Guru : Agar kalian lebih mudah mempelajari materi pada bab ini,sebaiknya segarkan kembali ingatan kalian dengan mengerjakan soal di bawah ini. : 1. 4 5 ? 8 15 ? ( a ) ( b )
- 2. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 48 - 2. Tentukan panjang jari jari lingkaran,jka diketahui kelilingnya adalah 11 cm ! 3. Tentukan panjang jari jari lingkaran,jika diketahui luasnya 19,635 cm2 !
- 3. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 49 - 8.1.1 Sifat sifat Garis Singgung Lingkaran Penjelasan Guru : PQ adalah tali busur terpanjang dan tegak lurus terhadap garis AB. Garis k berimpit dengan garis PQ,kemudian jika digeser meningalkan PQ dengan posisi yang selalu sejajar dengan tali busur PQ dan tegak lurus terhadap diameter AB atau jari-jari OB. Untuk mengetahui sifat-sifat garis singgung lingkaran.Ayo perhatikan penjelasan di bawah ini.! Kita akan menggeser garis k 1. Garis k sebelum digeser 2. Pada gambar di samping garis k i memotong lingkaran di dua titik yaitu P dan Q,begitu juga k ii juga memotong lingkaran di dua titik yaitu, R dan S 3. Pada gambar di samping garis k iii memotong lingkaran hanya pada satu titik dan tetap tegak lurus terhadap garis OB k P BA Q O k P BA Q O P BA Q O k i BA Q O k ii
- 4. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 50 -
- 5. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 51 - Pada kegiatan di atas garis k yang melalui titik B,yang menyinggung lingkaran,dan tegak lurus pada garis OB. Garis itulah yang disebut garis singgung lingkaran. Kesimpulan : 1. Garis singgung suatu lingkaran adalah suatu garis yang memotong lingkaran hanya pada satu titik. 2. Garis singgung suatu lingkaran tegak lurus terhadap jari-jari lingkaran yang melalui titik tersebut.
- 6. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 52 - 8.1.2 Melukis Garis Singgung Lingkaran Penjelasan Guru : a. Melukis Garis Singgung Lingkaran yang Melalui titik pada Lingkaran
- 7. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 53 - b. Melukis Garis Singgung Lingkaran yang Melalui Titik di Luar Lingkaran Penjelasan Guru :
- 8. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 54 -
- 9. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 55 - 8.1.3 Definisi dari Melukis Garis Singgung Definisi : Hanya ada SATU garis singgung pada titik A Hanya ada SATU garis singgung pada titik B Ada BANYAK garis singgung pada SEBUAH LINGKARAN Definisi Jika ada satu titik di luar lingkaran,maka hanya ada dua garis singgung yang melewati titik tersebut yang panjangnya sama ,,PK = PL = 2 panjang garis singgung
- 10. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 56 - Soal Ku !!! 1. Lukislah garis singgung pada lingkaran yang berpusat di titik O dan melewati titik A . 2. Lukislah garis singgung pada lingkaran yang berpusat di titik O dan melewati titik P 3. Lukislah garis singgung lingkaran dengan pusat O dari titik C di luar lingkaran dengan jari-jari lingkaran 3cm dan jaraknya OA 4cm ! A O . O P
- 11. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 57 - 8.1.4 Kedudukan Dua Lingkaran Pen jelasan Guru : Jika terdapat dua lingkaran masing-masing lingkaran satu berpusat di M dengan jari-jari r1 dan lingkaran dua berpusat di N dengan jari-jari r2 di mana r1 > r2 maka kedudukan lingkaran tersebut dapat dibedakan sebagai berikut: M, N M N M N M N M N M N MN = 0 d = l = MN < r1 MN > r2 d = l = MN > r1 + r2 MN < r1 MN >r2 d = 0 l = 2 MN = r1 - r2 MN < r2 MN = r2 d = 0 l = 0 MN > r1 + r2 MN < r1 MN >r2 d = 0 l = 2 MN > r1 + r2 MN > r1 MN >r2 d = 2 l = 2 Keterangan : MN = Garis yang menghubungkan kedua pusat lingkaran atau biasa disebut garis pusat atau garis sentral r1 = Jari-jari lingkaran yang besar r2 = Jari jari lingkaran kecil d = Garis singgung persekutuan dalam l = Garis singgung persekutuan luar
- 12. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 58 - 8.2 Panjang Garis Singgung Lingkaran 8.2.1 Panjang Garis Singgung Lingkaran Yang Ditarik Dari Titik Di Luar Lingkaran Penjelasan Guru : Pada gambar di samping, AB merupakan garis singgung lingkaran yang menyinggung lingkaran di titik B. Berdasarkan definisi yang sudah dipelajari sebelumnya diperoleh garis AB tegak lurus terhadap OB. Segitiga AOB siku-siku di B,maka : AO2 = OB2 + AB2 ( Teorema Pythagoras ) AB2 = OA2 + OB2 AB = OA 2 + OB2 O A B
- 13. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 59 - O Q A 8.2.2 Layang-layang Garis Singgung Penjelasan Guru : Pada gambar di samping PA dan PB adalah garis singgung lingkaran yang berpusat di titik O. Garis AB merupakan tali busur pada AOB, OA = OB = jari-jari.Jadi AOB adalah segitiga sama kaki. Pada ABP, DA = PB = garis singgung.Jadi ABP adalah segitiga sama kaki Soal Ku !!! 1. Pada gambar di atas OA = 16cm dan jarak OP = 30cm.Hitunglah panjang garis singgung AQ ! O A B P
- 14. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 60 - 2. Pada gambar di atas jari-jari OB = 6cm dan luas layang layang 48cm2 ! Hitunglah : a. Panjang OP b. Luas BOC c. Panjang diagonal AB 3. Pada gambar di atas LM adalah garis singgung lingkaran dan diketahui panjang OL 7cm. Berapakah jumlah panjang jumlah sisi berpenyikunya ? O A B P O L M 600 30 0
- 15. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 61 - 8.2.3 Garis Singgung persekutuan Penjelasan Guru : Pengertian : Garis singgung persekutuan adalah garis singgung yang menyinggung dua buah lingkaran sekaligus. Perhatikan gambar berikut : Gambar di atas merupakan garis singgung persekutuan dalam Gambar di atas merupakan garis singgung persekutuan luar M N P R M N K L
- 16. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 62 - a. Garis singgung persekutuan dalam b. Garis singgung persekutuan luar
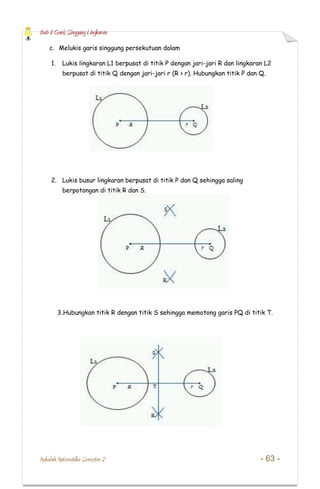
- 17. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 63 - c. Melukis garis singgung persekutuan dalam 1. Lukis lingkaran L1 berpusat di titik P dengan jari-jari R dan lingkaran L2 berpusat di titik Q dengan jari-jari r (R > r). Hubungkan titik P dan Q. 2. Lukis busur lingkaran berpusat di titik P dan Q sehingga saling berpotongan di titik R dan S. 3.Hubungkan titik R dengan titik S sehingga memotong garis PQ di titik T.
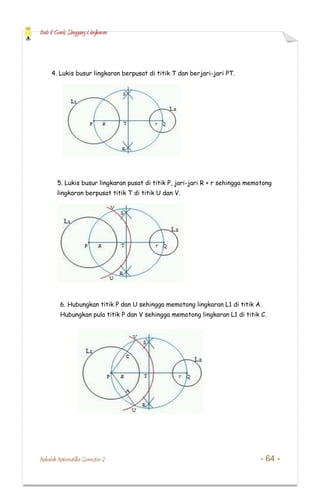
- 18. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 64 - 4. Lukis busur lingkaran berpusat di titik T dan berjari-jari PT. 5. Lukis busur lingkaran pusat di titik P, jari-jari R + r sehingga memotong lingkaran berpusat titik T di titik U dan V. 6. Hubungkan titik P dan U sehingga memotong lingkaran L1 di titik A. Hubungkan pula titik P dan V sehingga memotong lingkaran L1 di titik C.
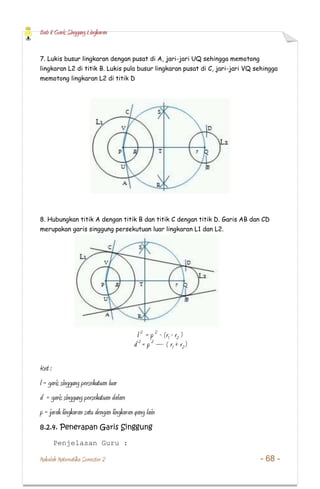
- 19. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 65 - 7. Lukis busur lingkaran pusat di titik A, jari-jari UQ sehingga memotong lingkaran L2 di titik B. Lukis pula busur lingkaran pusat di titik C jari-jari VQ sehingga memotong lingkaran L2 di titik D. 8. Hubungkan titik A dengan titik B dan titik C dengan titik D. Garis AB dan CD merupakan garis singgung persekutuan dalam lingkaran L1 dan L2.
- 20. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 66 - d. Melukis garis singgung persekutuan luar 1. Lukis lingkaran L1 dengan pusat di P berjari-jari R dan lingkaran L2 pusat di Q berjari-jari r (R > r). Hubungkan titik P dan Q. 2. Lukis busur lingkaran berpusat di titik P dan Q sehingga saling berpotongan di titik R dan S. 3. Hubungkan titik R dengan titik S sehingga memotong garis PQ di titik T.
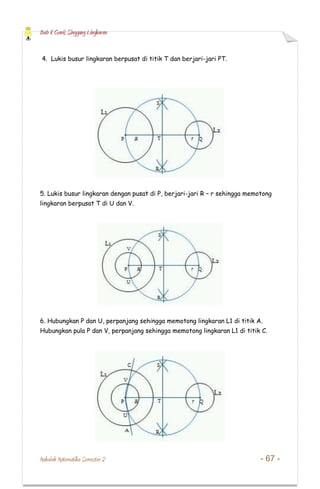
- 21. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 67 - 4. Lukis busur lingkaran berpusat di titik T dan berjari-jari PT. 5. Lukis busur lingkaran dengan pusat di P, berjari-jari R r sehingga memotong lingkaran berpusat T di U dan V. 6. Hubungkan P dan U, perpanjang sehingga memotong lingkaran L1 di titik A. Hubungkan pula P dan V, perpanjang sehingga memotong lingkaran L1 di titik C.
- 22. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 68 - 7. Lukis busur lingkaran dengan pusat di A, jari-jari UQ sehingga memotong lingkaran L2 di titik B. Lukis pula busur lingkaran pusat di C, jari-jari VQ sehingga memotong lingkaran L2 di titik D 8. Hubungkan titik A dengan titik B dan titik C dengan titik D. Garis AB dan CD merupakan garis singgung persekutuan luar lingkaran L1 dan L2. l 2 = p 2 - (r1 - r2 ) d 2 = p 2 ( r1 + r2) Ket : l = garis singgung persekutuan luar d = garis singgung persekutuan dalam p = jarak lingkaran satu dengan lingkaran yang lain 8.2.4. Penerapan Garis Singgung Penjelasan Guru :
- 23. Bab 8 Garis Singgung Lingkaran Makalah Matematika Semester 2 - 69 - Garis singgung dapat diterapkan di kehidupan sehari-hari contohnya seperti : - Mengikat drum - Mengikat beberapa paralon - Mengikat pipa air Contoh : 1. Gambar di bawah adalah penampang dari 2 buah pipa air berbentuk tabung dengan jari-jari 35cm.Berapakah tali minimal yang digunakan untuk mengikat tali tersebut ? Jawab : 1 Keliling lingkaran + 2x diameter