More Related Content
Similar to Computer Data Representation in Digital Format (20)
More from radianb (10)
Computer Data Representation in Digital Format
- 1. Arsitektur & Organisasi Komputer Representasi Data Komputer
- 2. Arsitektur & Organisasi Komputer Ada beberapa sistem bilangan yang digunakan dalam sistem digital yaitu sistem bilangan desimal, biner, oktal dan heksadesimal. Sistem bilangan desimal merupakan sistem bilangan yang paling familier dengan kita karena berbagai kemudahannya yang kita pergunakan sehari – hari. Komputer yang ada pada saat ini merupakan komputer biner. Semua bilangan yang disimpan dalam memori adalah data biner karena arsitektur komputer yang ada menggunakan sistem bilangan biner. Bilangan heksadesimal banyak digunakan dalam pemrograman bahasa assembly ataupun bahasa mesin.
- 3. Arsitektur & Organisasi Komputer Bilangan desimal adalah bilangan yang menggunakan basis 10 angka mulai 0,1,2,3,4,5,6,7,8,dan 9. Setelah angka 9, maka angka berikutnya adalah 10, 11, 12, 13, 14 dan seterusnya. Bilangan desimal disebut juga bilangan berbasis 10. Contoh penulisan bilangan desimal : 14(10). Ingat, desimal berbasis 10, maka angka 10-lah yang menjadi subscript pada penulisan bilangan desimal. System decimal merupakan positional value system dimana nilai dari sebuah digit bergantung pada posisinya. Sebagai contoh angka decimal 453. Digit 4 menyatakan 4 ratus, 5 menyatakan 5 puluh dan 3 menyatakan satuan. Contoh : 27.35 Bilangan ini sama dengan 2 puluhan ditambah 7 satuan ditambah 3 persepuluh ditambah 5 perseratus atau 2x10+7x1+3x0.1+5x0.01 BILANGAN DESIMAL
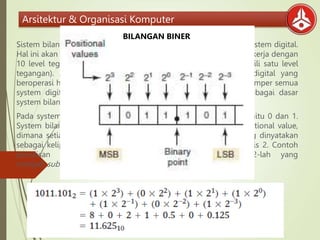
- 4. Arsitektur & Organisasi Komputer Sistem bilangan decimal kurang tepat diimplementasikan dalam system digital. Hal ini akan sangat sulit merangcang perangkat elektronik yang bekerja dengan 10 level tegangan berbeda dimana satu karakter decimal mewakili satu level tegangan). Akan sangat mudah untuk merancang rangkaian digital yang beroperasi hanya dengan 2 level tegangan. Karena alasan inilah hamper semua system digital menggunakan system bilangan biner (base 2) sebagai dasar system bilangan untuk operasinya. Pada system bilangan biner terdapat 2 simbol atau nilai digit yaitu 0 dan 1. System bilangan biner juga merupakan sebuah system yang positional value, dimana setiap digit bilangan biner memiliki nilainya sendiri, yang dinyatakan sebagai kelipatan 2. Bilangan biner juga disebut bilangan berbasis 2. Contoh penulisan : 1001(2). Biner berbasis 2, maka angka 2-lah yang menjadi subscript pada penulisan bilangan desimal. BILANGAN BINER
- 5. Arsitektur & Organisasi Komputer BILANGAN BINER
- 6. Arsitektur & Organisasi Komputer Bilangan heksadesimal, atau bilangan heksa, atau bilangan basis 16 adalah bilangan yang menggunakan 16 buah simbol, mulai dari angka 0,1,2,3,4,5,6,7,8, dan 9, kemudian dilanjut huruf A,B,C,D,E, dan F. Jadi, huruf A sampai F merupakan simbol untuk mengganti angka 10 sampai 15. Contoh penulisan : E316. Hexadesimal berbasis 16, maka angka 16-lah yang menjadi subscript pada penulisan bilangan desimal.
- 7. Arsitektur & Organisasi Komputer Konversi Radiks-r ke desimal ■Rumus konversi radiks-r ke desimal: ■Contoh: ■11012 = 1×23 + 1×22 + 1×20 = 8 + 4 + 1 = 1310 ■2A16 = 2×161 + 10×160 = 32 + 10 = 4210
- 8. Arsitektur & Organisasi Komputer Konversi Bilangan Desimal ke Biner ■Konversi bilangan desimal ke bilangan Biner: Gunakan pembagian dgn 2 secara suksesif sampai sisanya = 0. Sisa-sisa pembagian membentuk jawaban, yaitu sisa yang pertama akan menjadi least significant bit (LSB) dan sisa yang terakhir menjadi most significant bit (MSB). ■Contoh: Konversi 17910 ke biner: ■179 / 2 = 89 sisa 1 (LSB) ■/ 2 = 44 sisa 1 ■/ 2 = 22 sisa 0 ■/ 2 = 11 sisa 0 ■/ 2 = 5 sisa 1 ■/ 2 = 2 sisa 1 ■/ 2 = 1 sisa 0 ■/ 2 = 0 sisa 1 (MSB) ■⇒ 17910 = 101100112 ■■MSB LSB
- 9. Arsitektur & Organisasi Komputer Konversi Bilangan Desimal ke Hexadesimal ■Konversi bilangan desimal bulat ke bilangan hexadesimal: Gunakan pembagian dgn 16 secara suksesif sampai sisanya = 0. Sisa-sisa pembagian membentuk jawaban, yaitu sisa yang pertama akan menjadi least significant bit (LSB) dan sisa yang terakhir menjadi most significant bit (MSB). ■Contoh: Konversi 17910 ke hexadesimal: ■179 / 16 = 11 sisa 3 (LSB) ■/ 16 = 0 sisa 11 (dalam bilangan hexadesimal berarti B)MSB ■⇒ 17910 = B316
- 10. Arsitektur & Organisasi Komputer Konversi Bilangan Biner ke Hexadesimal Untuk mengkonversi bilangan biner ke bilangan hexadesimal, lakukan pengelompokan 4 digit bilangan biner dari posisi LSB sampai ke MSB â– Contoh: konversikan 101100112 ke bilangan hexa â– Jawab : 1011 0011 â– B 3 â– Jadi 101100112 = B316
- 11. Arsitektur & Organisasi Komputer Konversi Bilangan Hexadesimal ke Biner Sebaliknya untuk mengkonversi Bilangan Hexadesimal ke Biner yang harus dilakukan adalah terjemahkan setiap digit bilangan Hexadesimal ke 4 digit bilangan biner â– Contoh Konversikan B316 ke bilangan biner. â– Jawab: B 3 â– 1011 0011 â– Jadi B316 = 101100112
- 12. Arsitektur & Organisasi Komputer LATIHAN ■8910 = ……16 ■110102 = ……10 ■29A16 = ……10 ■35910 = ……2 ■7510 = ……16 ■101012 = ……10 ■10B16 = ……10 ■20710 = ……2 ■2610 = ……16 ■011012 = ……10 ■83C16 = ……10 ■41410 = ……2 ■3110 = ……16 ■100102 = ……10 ■75D16 = ……10 ■19510 = ……2 ■9410 = ……16 ■100102 = ……10 ■38F16 = ……10 ■48210 = ……2 ■5810 = ……16 ■001102 = ……10 ■49F16 = ……10 ■23710 = ……2 ■9210 = ……16 ■010012 = ……10 ■8F116 = ……10 ■31010 = ……2