�ݺ�ߣ

Kelompok 2
1. Alfi Wahdatul Ilmi
2. GinaAmalia
3. M.AbdulAziz
4. Nisa FauziahA.
5. QorryA. Pitria
6. Rifki Insani Taufik

Variabel Acak
Kontinu
Varibel acak kontinu adalah variabel acak
yang mengambil seluruh nilai yang ada dalam
sebuah interval atau variabel yang dapat
memiliki nilai-nilai pada suatu interval tertentu.
Nilainya dapat merupakan bilangan bulat
maupun pecahan. Varibel acak kontinu jika
digambarkan pada sebuah garis interval, akan
berupa sederetan titik yang bersambung
membantuk suatu garis lurus.

Distribusi probalitas untuk variabel acak kontinu
(kurva beraturan) tidak dapat disajikan dalam bentuk tabel,
tetapi dinyatakan dalam kurva y = f(x) dengan f(x)
merupakan nilai-nilai variabel acak kontinu yang dilukiskan
sebagai grafik kurva f(x) berikut ini.
Gambar 1. Luas Kurva y = f(x) pada x1 = a dan x2 = b

Fungsi probabilitas variable acak kontinu pada
Gambar 1 merupakan luas daerah dibawah kurva
yang dibatasi oleh interval 𝑎 ≤ 𝑥 ≤ 𝑏 , yang
dinyatakan oleh luas daerah yang diarsir berikut ini:
𝒃
𝑷 𝒂 ≤ 𝒙 ≤ 𝒃 = ∫ 𝒇 𝒙 𝒅𝒙
𝒂
Khusus untuk kurva y = f(x) yang berbentuk kurva
lurus beraturan dapat juga dihitung berdasarkan
formula ulas bidang datar yang terjadi.

Sebuah variable (peubah) acak kontinu X
untuk nilai-nilai di antara x = 1 dan x = 5
dinyatakan dengan, fungsi probabilitas
𝑓 𝑥 =
𝑥 + 2
20
a) Buktikanlah P(1 < X < 5) = 1.
b) Hitunglah P(X < 3).
c) Hitunglah P(2 < X < 4,5).

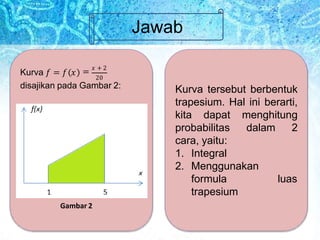
Jawab
Kurva 𝑓 = 𝑓 𝑥 = 𝑥 + 2
20
disajikan pada Gambar 2:
Gambar 2
Kurva tersebut berbentuk
trapesium. Hal ini berarti,
kita dapat menghitung
probabilitas dalam 2
cara, yaitu:
luas
1. Integral
2. Menggunakan
formula
trapesium

a) Buktikan P(1 < X < 5)
= 1
Cara 1: (Integral)
1 20
P(1 < X < 5) = ∫
5 𝑥 + 2
𝑑𝑥
1
20 1 2
1 1 2
( . 5 + 2 . 5) − (
1
2
2
. 1 + 2 . 1)
20 2
1
(25
+ 10 −
1
2
− 2)
= [5 1
𝑥2 + 2𝑥)
=
=
=
20 2
1
20
(12 + 8) = 1
∴ P(1 < X < 5) = 1 (Terbukti)

Cara 2: (Menggunakan formula luas
trapesium)
Formula luas trapesium = (5 – 1)
2
𝑓 1 +𝑓(5)
,
3
20 20 20
dengan f(1) = 1+2
= dan f(5) = 5+2
=
20
7
.
Hal ini berarti:
P(1 < X < 5) = 4
7
3
+
20 20
2
= 2
10
20
= 1
∴ P(1 < X < 5) = 1 (Terbukti)

b) Hitunglah P(X < 3)
20
P(X < 3) = P(1 < x < 3)
= ∫
3 𝑥 + 2
𝑑𝑥
1
1
20 1 2
1 1 2
( . 3 + 2 . 3) − (
1
2
2
. 1 + 2.1)
20 2
1
(9
+ 6 −
20
= [3 1
𝑥2 + 2𝑥)
=
=
20 2
= 1
(4+4) =
1
2
8
20
− 2)
= 0,4
∴ P(X < 3) = 0,4

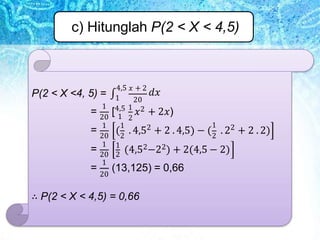
c) Hitunglah P(2 < X < 4,5)
P(2 < X <4, 5) = ∫1 20
4,5 𝑥 + 2
𝑑𝑥
1
1 2
20
1 1 1
2 2
( . 4,5 + 2 . 4,5) − ( . 2 + 2 . 2)
20 2 2
1 1
(4,52−22) + 2(4,5 − 2)
= [4,5 1
𝑥2 + 2𝑥)
=
=
=
20 2
1
20
(13,125) = 0,66
∴ P(2 < X < 4,5) = 0,66

�ݺ�ߣ

distribusivariabelacakkontinyu2222-171219030106 (1).pptx

Recommended

More Related Content

Similar to distribusivariabelacakkontinyu2222-171219030106 (1).pptx (20)

Recently uploaded (20)

distribusivariabelacakkontinyu2222-171219030106 (1).pptx