Formule geometrie
- 1. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 39 BREVIAR TEORETIC CU EXEMPLE CONCRETE, PENTRU PREGÄTIREA EXAMENULUI DE EVALUARE NAÅĒIONALÄ, clasa a VIII-a - 2010 PropunÄtor: Prof. IGNÄTESCU VIOREL OVIDIU Åcoala cu clasele I-VIII MÄteÅti, com. SÄpoca, jud. BuzÄu V. 1. MÄsurare Åi mÄsuri (lungime, arie, volum, masÄ, capacitate, timp) Unitatea de mÄsurÄ pentru lungime este metrul (m). El are multiplii urmÄtori : decametrul (dam), hectometrul (hm), kilometrul (km) Åi submultiplii urmÄtori: decimetrul (dm), centimetrul (cm), milimetrul (mm). Multiplii Unitatea principala m Submultiplii km hm dam dm cm mm 0,001 0,01 0,1 1 10 100 1000 1 10 102 103 104 105 106 Ex. de transformÄri: 321,15 dm = 32,115 m= 3211,5 cm = 32115 mm; 9485 m=948,5 dam= 94,85 hm=9,485 km. Perimetrul pÄtratului P = 4l ; perimetrul dreptunghiului P= 2l +2L. Unitatea principalÄ pentru mÄsurarea suprafeÅĢelor este metrul pÄtrat (m2 ), care reprezintÄ aria unui pÄtrat cu latura de 1m. Multiplii sunt :dam2 , hm2 , km2 . Submultiplii sunt : dm2 , cm2 , mm2 . Multiplii Unitatea principala m2 Submultiplii km2 hm2 dam2 dm2 m2 mm2 10-6 10-4 10-2 1 102 104 106 Ex. de transformÄri : 2,75 hm2 =275 dam2 =0,0275 km2 15,25 dm2 =152500 mm2 =1525 cm2 1 hectar =1 ha =1 hm2 1 ar = 1 dam2 Aria pÄtratului A =l2 ; Aria dreptunghiului A =l·L. Unitatea principalÄ pentru mÄsurarea volumului este metrul cub (m3 ), care reprezintÄ volumul unui cub cu latura de 1 m. Multiplii Unitatea principala m3 Submultiplii km3 hm3 dam3 dm3 cm3 mm3 10-9 10-6 10-3 1 103 106 109 Ex. 0,021 dm3 =21 cm3 =21000 mm3 49 dam3 =0,049 hm3 =49000 m3 Volumul cubului V =l3 Revista Mateinfo.ro ISSN 2065 â 6432 nr. ianuarie 2010
- 2. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 40 Volumul paralelipipedului dreptunghic : V =l·L·h. Unitatea de mÄsura a capacitÄÅĢii (volumul ocupat de un lichid) este litrul (l) . 1l =1 dm3 . Multiplii Unitatea principala l Submultiplii kl hl dal dl cl ml 0,001 0,01 0,1 1 10 100 1000 Ex. 145 l = 1,45 hl =14500 cl 4,18 hl =0,418 kl =418 l =41800 cl. Unitatea principalÄ de mÄsurÄ pentru masÄ este gramul (g) care are submultiplii : dg, cg, mg Åi multiplii :dag, hg, kg. Multiplii Unitatea principala g Submultiplii kg hg dag dg cg mg 0,001 0,01 0,1 1 10 100 1000 Ex. 25,3 hg =253 dag =2,53 kg =2530 g Unitatea principalÄ de mÄsura pentru timp este secunda (s). 1 ora (h) =60 minute (min) =3600 secunde (s) Ex. 372 s =60 min 12 s 0,4 h =0,4x60 min =24 min =24x60 s = 1440 s 48 min 27 s + 5h 56 s = 5h 48 min 83 s = 5h 49 min 23 s V. 2. Dreapta Punctul, dreapta Åi planul sunt noÅĢiuni geometrice fundamentale care nu se definesc. x A â punct âplan âdreapta Îą d Axioma dreptei: prin douÄ puncte distincte trece o dreaptÄ Åi numai una.
- 3. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 41 Vom scrie A, B âd, Câd. DouÄ drepte pot fi : concurente (cÃĒnd au un singur punct comun), paralele (dacÄ nu au nici un punct comun, dar fac parte din acelaÅi plan), necoplanare (dacÄ nu sunt situate ÃŪn acelaÅi plan). Semidreapta este o parte dintr-o dreaptÄ, limitatÄ de un punct numit origine. Segmentul este mulÅĢimea punctelor de pe o dreaptÄ aflate ÃŪntre douÄ puncte ale dreptei, numite capete. Lungimea segmentului este distanÅĢa dintre capetele segmentului. DouÄ segmente se numesc congruente dacÄ au aceeaÅi lungime. Mijlocul unui segment este punctul care ÃŪmparte segmentul ÃŪn douÄ segmente congruente. Trei sau mai multe puncte se numesc coliniare dacÄ aparÅĢin aceleiaÅi drepte. Se numesc puncte coplanare punctele care se aflÄ ÃŪn acelaÅi plan. O dreaptÄ poate fi : conÅĢinutÄ ÃŪntr-un plan (dacÄ cel puÅĢin 2 puncte ale ei aparÅĢin planului), paralelÄ cu planul (dacÄ ea nu are puncte comune cu planul), incidentÄ ( dacÄ are un singur punct comun cu planul). V. 3. Unghiul Figura geometricÄ formatÄ din douÄ semidrepte care au originea comunÄ se numeÅte unghi. Unghiul poate fi : nul (cÃĒnd laturile sale coincid), alungit (cÃĒnd laturile sunt semidrepte opuse), propriu (cÃĒnd nu e nici nul, nici alungit). Masura unui unghi este datÄ de deschiderea dintre laturile sale. Unitatea de mÄsura a unghiului se numeÅte grad (sexagesimal) cu multiplii : minutul (10 =60â) Åi secunda (1â=60ââ). Instrumentul de mÄsurÄ este raportorul. Unghiul poate fi : ascuÅĢit (cÃĒnd mÄsura sa este mai micÄ de 900 ), obtuz (cÃĒnd mÄsura sa este mai mare de 900 ) sau drept (cÃĒnd are 900 ). Ex. a) 620 45â57ââ +180 29â36ââ= 800 74â93ââ= 810 14â93ââ= =810 15â33ââ b) 1350 18â12ââ â 420 36â25ââ=1340 77â72ââ - 420 36â25ââ= 920 41â47ââ c) 3 ·140 53ââ=420 159ââ=420 2â39ââ d) 1250 : 4=1240 60â : 4=310 15â DouÄ unghiuri care au mÄsurile egale se numesc unghiuri congruente. DouÄ unghiuri proprii care au vÃĒrful comun Åi o laturÄ comunÄ situatÄ ÃŪn interiorul unghiului format de cele douÄ unghiuri se numesc unghiuri adiacente.
- 4. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 42 Bisectoarea unui unghi propriu este semidreapta cu originea ÃŪn vÃĒrful unghiului, situatÄ ÃŪn interiorul acestuia, care formeazÄ cu laturile unghiului iniÅĢial douÄ unghiuri congruente. DouÄ unghiuri se numesc suplementare dacÄ suma mÄsurilor lor este de 1800 . DouÄ unghiuri se numesc complementare dacÄ suma mÄsurilor lor este de 900 . Ex. Suplementul unghiului de 750 29â17ââ este 1800 -750 29â17ââ=1790 59â60ââ-750 29â17ââ=1040 30â43ââ Complementul sÄu este 900 -750 29â17ââ=890 59â60ââ-750 29â17ââ=140 30â43ââ DouÄ unghiuri cu acelaÅi vÃĒrf care au laturile unuia ÃŪn prelungirea laturilor celuilalt se numesc unghiuri opuse la vÃĒrf. DouÄ unghiuri opuse la vÃĒrf sunt congruente. Suma mÄsurilor unghiurilor formate ÃŪn jurul unui punct este de 3600 . V. 4. CongruenÅĢa triunghiurilor ; perpendicularitate ÃŪn plan ; paralelism Figura geometricÄ formatÄ din cele trei segmente determinate de trei puncte necoliniare se numeÅte triunghi. Suma lungimilor laturilor unui triunghi se numeÅte perimetrul triunghiului (P), iar jumÄtatea acestuia este semiperimetrul (p). DupÄ laturi triunghiul poate fi: scalen (laturile au mÄsuri diferite), isoscel (douÄ laturi sunt congruente), echilateral (toate laturile sunt congruente). DupÄ unghiuri triunghiul poate fi: ascuÅĢitunghic (toate unghiurile sunt ascuÅĢite), dreptunghic (un unghi este drept), obtuzunghic (un unghi este obtuz). Suma mÄsurilor unghiurilor ÃŪn orice triunghi este de 1800 . Unghiul care este adiacent Åi suplementar cu un unghi al unui triunghi se numeÅte unghi exterior al triunghiului. DouÄ triunghiuri sunt congruente dacÄ laturile triunghiurilor sunt respectiv congruente Åi unghiurile sunt respectiv congruente. Cazurile de congruenÅĢÄ pentru triunghiuri oarecare: -L.U.L. (laturÄ-unghi-laturÄ) -U.L.U. (unghi-laturÄ-unghi) -L.L.L. (laturÄ-laturÄ-laturÄ) DatoritÄ criteriului 2 Åi faptului cÄ suma mÄsurilor unghiurilor ÃŪn triunghi este 1800 , se poate enunÅĢa -L.U.U. (laturÄ-unghi-unghi) Metoda triunghiurilor congruente ajutÄ la demonstrarea congruenÅĢei a douÄ laturi sau douÄ unghiuri pe care trebuie sÄ le ÃŪncadram ÃŪn triunghiri despre care se va arÄta cÄ sunt congruente (conform unuia din cazurile de congruenÅĢÄ). Ex. Ãn figura urmÄtoare âĒABC âĄâĒDCB Åi âĒACB ⥠âĒDBC. DemonstrÄm cÄ âĒBAC âĄâĒBDC Åi [AC]⥠[BD].
- 5. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 43 Privim ÎABC Åi ÎDCB. Avem âĒACB ⥠âĒDBC (ipotezÄ), [BC]âĄ[BC] (lat. comunÄ) Åi âĒABC âĄâĒDCB (ipotezÄ) â(conform U.L.U.) ÎABC ⥠ÎDCB ââĒBAC âĄâĒBDC Åi [AC]⥠[BD]. DouÄ drepte concurente sunt perpendiculare dacÄ unul din unghiurile ce se formeazÄ ÃŪn jurul punctului lor comun este unghi drept (d âĨ g). Fiind dat un punct A exterior dreptei d, atunci punctul B â d a. ÃŪ. AB âĨ d se numeÅte piciorul perpendicularei din A pe d. DistanÅĢa de la un punct exterior unei drepte la dreaptÄ este distanÅĢa dintre punct Åi piciorul perpendicularei duse din acel punct pe dreaptÄ d( A, d) = AB. Criteriile de congruenÅĢÄ ale triunghiurilor dreptunghice : -C. C. (catetÄ-catetÄ) -C. U. ( catetÄ-unghi) -I. U. (ipotenuzÄ-unghi) I. C. (ipotenuzÄ-catetÄ) Proprietatea bisectoarei : un punct din interiorul unui unghi propriu aparÅĢine bisectoarei unghiului dacÄ Åi numai dacÄ DistanÅĢele de la punct la laturile unghiului sunt egale. ConcurenÅĢa bisectoarelor ÃŪntr-un triunghi : ÃŪn orice triunghi cele trei bisectoare sunt concurente ( punctul lor de intersecÅĢie este centrul cercului ÃŪnscris ÃŪn triunghi). Mediatoarea unui segment este dreapta perpendicularÄ pe segment ÃŪn mijlocul acestuia. Proprietatea mediatoarei : un punct aparÅĢine mediatoarei unui segment dacÄ Åi numai dacÄ are distanÅĢele egale faÅĢÄ de extremitÄÅĢile segmentului. ConcurenÅĢa mediatoarelor : ÃŪn orice triunghi mediatoarele celor trei laturi sunt concurente ( punctul lor de intersecÅĢie este centrul cercului circumscris triunghiului). DouÄ drepte sunt paralele dacÄ sunt coplanare Åi nu au nici un punct comun. Axioma paralelelor (Euclid) : printr-un punct exterior unei drepte date, trece o singurÄ paralelÄ la dreapta datÄ. DouÄ drepte intersectate cu o secantÄ formeazÄ o pereche de unghiuri alterne interne congruente, dacÄ Åi numai dacÄ dreptele sunt paralele.
- 6. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 44 dâ || dââ â âĒ 1âĄâĒ2 Ãntr-un triunghi, segmentul care uneÅte mijloacele a douÄ laturi se numeÅte linie mijlocie a triunghiului Åi ea are proprietatea cÄ e paralelÄ cu cea de-a treia laturÄ Åi jumÄtate din lungimea acesteia. MN linie mijlocieâ MNâĨBC Åi 2MN=BC V. 5. ProprietÄÅĢi ale triunghiurilor Suma mÄsurilor unghiurilor unui triunghi este 1800 . MÄsura unui unghi exterior unui triunghi este egalÄ cu suma mÄsurilor celor douÄ unghiuri ale triunghiului neadiacente cu el. O ÃŪnÄlÅĢime a unui triunghi este segmental determinat de un vÃĒrf al triunghiului Åi piciorul perpendicularei dusÄ din acel vÃĒrf pe latura opusÄ. ÃnÄlÅĢimile ÃŪn orice triunghi sunt concurente, iar punctul lor comun se numeÅte ortocentrul triunghiului (H). Segmentul determinat de un vÃĒrf al unui triunghi Åi mijlocul laturii opuse se numeÅte medianÄ. Medianele ÃŪn orice triunghi sunt concurente; punctul lor comun se numeÅte centrul de greutate al triunghiului Åi se aflÄ la 2 treimi de vÃĒrf Åi o treime de bazÄ. GB=2/3 BM ; GM=1/3 BM. ProprietÄÅĢile triunghiului isoscel : -ÃŪntr-un triunghi isoscel unghiurile alÄturate bazei sunt congruente -ÃŪntr-un triunghi isoscel bisectoarea unghiului din vÃĒrf, ÃŪnÄlÅĢimea Åi mediana corespunzÄtoare bazei coincid Åi sunt incluse ÃŪn mediatoarea bazei -medianele laturilor congruente sunt congruente (analog pentru ÃŪnÄlÅĢimi, bisectoare) ProprietÄÅĢile triunghiului echilateral :
- 7. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 45 -ÃŪntr-un triunghi echilateral toate unghiurile sunt congruente (au 600 ) -ÃŪntr-un triunghi echilateral mediana, bisectoarea Åi ÃŪnÄlÅĢimea fiecÄrei laturi coincid Åi sunt incluse ÃŪn mediatoarea laturii respective. ProprietÄÅĢile triunghiului dreptunghic : -ÃŪntr-un triunghi dreptunghic isoscel unghiurile alÄturate bazei au fiecare 450 -ÃŪntr-un triunghi dreptunghic lungimea medianei corespunzÄtoare ipotenuzei este egalÄ cu jumÄtate din lungimea ipotenuzei -ÃŪntr-un triunghi dreptunghic cateta care se opune unghiului de 300 este jumÄtatea ipotenuzei -centrul cercului circumscris triunghiului dreptunghic ( intersecÅĢia mediatoarelor) se aflÄ la mijlocul ipotenuzei -ortocentrul unui triunghi dreptunghic este vÃĒrful triunghiului drept. V. 6. Patrulatere. Arii Suma mÄsurilor unui patrulater convex este este egalÄ cu 3600 . Paralelogramul este patrulaterul convex cu laturile opuse paralele. Dreptunghiul este paralelogramul cu un unghi drept. Rombul este paralelogramul cu douÄ laturi consecutive congruente. PÄtratul este dreptunghiul cu douÄ laturi consecutive congruente (sau este rombul cu un unghi drept).
- 8. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 46 Trapezul este patrulaterul convex cu douÄ laturi paralele numite baze Åi doua neparalele. Segmentul care uneÅte mijloacele laturilor neparalele se numeÅte linie mijlocie ÃŪn trapez; este paralelÄ cu bazele Åi egalÄ cu semisuma lor. ProprietÄÅĢile paralelogramului : -laturile opuse sunt congruente -unghiurile opuse sunt congruente -unghiurile alÄturate sunt suplementare -diagonalele au acelaÅi mijloc ProprietÄÅĢile dreptunghiului : -are toate proprietÄÅĢile paralelogramului -toate unghiurile au 900 -diagonalele sunt congruente ProprietÄÅĢile rombului : -are toate proprietÄÅĢile paralelogramului -are toate laturile congruente -diagonalele sunt perpendiculare Åi sunt bisectoarele unghiurilor ProprietÄÅĢile pÄtratului : -are toate proprietÄÅĢile dreptunghiului Åi ale rombului Arii : -aria triunghiului A= 2 hB â -aria triunghiului dreptunghic A= 2 21 cc â -aria paralelogramului A=B·h -aria dreptunghiului A=l·L -aria rombului A= B·h = 2 Dd â -aria pÄtratului A=l2 -aria trapezului A= 2 )( hbB â + V. 7. AsemÄnarea triunghiurilor Teorema paralelelor echidistante : DacÄ dreptele paralele d1, d2, ..., dn determinÄ pe o secantÄ segmente congruente, atunci ele determinÄ pe orice altÄ secantÄ segmente congruente. Teorema lui Thales : O paralelÄ dusÄ la una din laturile unui triunghi determinÄ pe celelalte douÄ laturi segmente proporÅĢionale.
- 9. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 47 MN âĨBC â NCMB = ANAM Teorema paralelelor neechidistante : Dreptele paralele d1, d2, ..., dn determinÄ pe douÄ secante oarecare segmente proporÅĢionale. Teorema bisectoarei :Ãntr-un triunghi bisectoarea unui unghi determinÄ pe latura opusÄ douÄ segmente proporÅĢionale cu laturile unghiului. [AD bisectoarea âĒBAC â ACDC = ABBD Teorema fundamentalÄ a asemÄnÄrii : O paralelÄ la una din laturile unui triunghi formeazÄ cu celelalte douÄ laturi un triunghi asemenea cu cel dat. MN âĨ BC â Î ABC â― Î AMN Criteriile de asemÄnare : -cazul I : douÄ triunghiri sunt asemenea dacÄ au douÄ unghiuri respectiv congruente ; -cazul II : douÄ triunghiri sunt asemenea dacÄ au 2 laturi respecriv proporÅĢionale Åi unghiurile dintre aceste laturi congruente ; -cazul III : douÄ triunghiuri sunt asemenea dacÄ au laturile respectiv proporÅĢionale. V. 8. RelaÅĢii metrice ÃŪn triunghiul dreptunghic Teorema ÃŪnÄlÅĢimii: Ãntr-un triunghi dreptunghic lungimea ÃŪnÄlÅĢimii corespunzÄtoare ipotenuzei este media geometricÄ a lungimilor proiecÅĢiilor catetelor pe ipotenuzÄ. BD2 = AD ·DC Teorema catetei: Ãntr-un triunghi dreptunghic lungimea unei catete este media geometricÄ a lungimii proiecÅĢiilor sale pe ipotenuzÄ Åi a lungimii ipotenuzei.
- 10. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 48 AB2 = AD ·DC; BC2 = DC ·AC Teorema lui Pitagora: Ãntr-un triunghi dreptunghic pÄtratul lungimii ipotenuzei este egal cu suma pÄtratelor lungimilor catetelor. AC2 = AB2 +BC2 Definirea funcÅĢiilor trigonometrice: sinus(sin) = cateta opusÄ / ipotenuzÄ cosinus(cos)= cateta alÄturatÄ / ipotenuzÄ tangenta(tg) = cateta opusÄ /cateta alÄturatÄ cotangenta(ctg) = cateta alÄturatÄ / cateta opusÄ Formula fundamentalÄ a trigonometriei: sin2 x +cos2 x =1 Valori ale funcÅĢiilor trigonometrice pentru cÃĒteva unghiuri: sin cos tg ctg 300 2 1 2 3 3 3 3 450 2 2 2 2 1 1 600 2 3 2 1 3 3 3 CÃĒteva formule de trigonometrie: cos x =sin ( 90-x); tg x = sin x / cos x; ctg x =1 / tg x; ctg x = tg (90-x) Aria unui triunghi: A= 2 sin BBCAB â â ; A = 2 cos 2 sinBCAB BB â â ; A= ))()( cpbpa ââ( pp â , unde a, b, c sunt laturile triunghiului, iar 2 p = cba ++ . 4 32 l A = (pentru triunghiul echilateral) Raza cercului ÃŪnscris ÃŪntr-un triunghi: r = p S Raza cercului circumscris unui triunghi : R = S4 abc V. 9. Cercul. Poligoane regulate 1=centrul cercului
- 11. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 49 =coarda e centrul cercului, iar laturile sunt raze) : mÄsura este egalÄ cu mÄsura e cerc, iar laturile sunt coarde) : mÄsura este egalÄ cu jumÄtatea t coarde) : mÄsura este iar laturile sunt coarde) : mÄsura este uprinse ÃŪntre laturi. Åi tangenta ÃŪntr-un punct sunt perpendiculare) de o diagonalÄ cu o laturÄ este ate laturile Åi toate unghiurile congruente. at. Calculul elementelor ÃŪn poligoane regulate: ra aria 2=diametrul 3=raza 4 Unghiuri ÃŪn cerc: -unghi la centru (vÃĒrful est arcului cuprins ÃŪntre laturi. -unghi ÃŪnscris ÃŪn cerc (vÃĒrful este p mÄsurii arcului cuprins ÃŪntre laturi. -unghi cu vÃĒrful ÃŪn interior (vÃĒrful este ÃŪn interiorul cercului, iar laturile sun egalÄ cu semisuma mÄsurilor arcelor cuprinse ÃŪntre laturi Åi prelungirile lor. -unghi cu vÃĒrful ÃŪn exterior (vÃĒrful este ÃŪn exteriorul cercului, egalÄ cu semidiferenÅĢa mÄsurilor arcelor c PoziÅĢiile unei drepte faÅĢÄ de cerc : -secantÄ : are douÄ puncte comune cu cercul -tangentÄ : are un punct comun cu cercul ( raza -exterioarÄ : nu are puncte comune cu cercul. Patrulatere inscriptibile (cu vÃĒrfurile pe un cerc) ; proprietÄÅĢi : -un patrulater este inscriptibil dacÄ Åi numai dacÄ unghiurile sale opuse sunt suplementare -un patrulater este inscriptibil dacÄ Åi numai dacÄ unghiul format congruent cu unghiul format de cealaltÄ diagonalÄ cu latura opusÄ. Un poligon regulat este poligonul convex cu to Ex : triunghiul echilateral, pÄtratul, hexagonul regul latu apotema(=r) triunghi echilateral R 3 2 R 4 33 2 R pÄtrat R 2 2R2 2R2 hexagon regulat R 2 3R 2 33 2 R unde R=raza cercului circumscris, iar r= raza cercului ÃŪnscris. 2Ï·R Aria discului : A= Ï R2 . . 10. Puncte, drepte, plane.Paralelism ÃŪn spaÅĢiu Lungimea cercului : L = V determinat de: care nu-i aparÅĢine ouÄ d clid : Printr-un punct exterior unei drepte se poate duce o paralelÄ Åi numai ice plan care conÅĢine dreapta Åi-l intersecteazÄ pe Un plan poate fi -trei puncte necoliniare -o dreaptÄ Åi un punct -douÄ drepte paralele -d repte concurente Axioma lui Eu una la dreapta datÄa. Teoreme de paralelism : -dacÄ o dreaptÄ este paralelÄ cu un plan, atunci or primul o face dupÄ o dreaptÄ paralelÄ cu cea datÄ.
- 12. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 50 plan conÅĢine douÄ drepte concurente care sunt paralele cu un alt plan, atunci planele sunt ane paralele determinÄ pe douÄ drepte oarecare pe care le intersecteazÄ segmente roporÅĢionale. . 11. Perpendicularitate ÃŪn spaÅĢiu -dÃĒndu-se douÄ plane paralele, orice dreaptÄ dintr-unul este paralelÄ cu celÄlalt. -dacÄ un plan intersecteazÄ douÄ plane paralele, atunci dreptele de intersecÅĢie sunt paralele. -dacÄ un paralele. - douÄ plane paralele cu un al treilea plan sunt paralele ÃŪntre ele. - mai multe pl p V este perpendicularÄ pe douÄ drepte concurente din plan, atunci ea este e l cu piciorul celei de a doua perpendiculare este onÅĢinutÄ ÃŪn plan. e unghi ascuÅĢit sau drept cu vÃĒrful ÃŪn umim unghi al unei drepte cu un plan unghiul pe care acea dreaptÄ ÃŪl face cu proiecÅĢia ei Åte unghi diedru figura geometricÄ formatÄ de douÄ semiplane delimitate de planele ce formeazÄ diedrul avÃĒnd originea pe muchia diedrului Åi fiind erpendicularÄ pe acestea. . 12. Poliedre Se numesc drepte perpendiculare douÄ drepte care formeazÄ un unghi drept. DacÄ o dreaptÄ perpendicularÄ pe plan. Teoreme : -douÄ plane perpendiculare pe aceeaÅi dreaptÄ sunt paralel -douÄ drepte perpendiculare pe acelaÅi plan sunt paralele -teorema celor trei perpendiculare : dacÄ dintr-un punct exterior unui plan se duce o perpendicularÄ pe acel plan, iar din piciorul acesteia se duce o perpendicularÄ pe o dreaptÄ conÅĢinutÄ ÃŪn plan, atunci dreapta ce uneÅte punctu perpendicularÄ pe dreapta c Unghiuri ÃŪn spaÅĢiu: Prin unghiul a douÄ drepte ÃŪn spaÅĢiu ÃŪnÅĢelegem oric orice punct al spaÅĢiului Åi cu laturile paralele cu dreptele date. N pe plan. Se nume aceeaÅi dreaptÄ. Se numeÅte unghi plan asociat unui unghi diedru unghiul determinat de douÄ semidrepte conÅĢinute respectiv ÃŪn semi p V = -cubul: A=6l2 l3 V= d 3l a l dreptunghic: +hl) 2 =l2 +L2 +h2 -p ralelipipedu Alat =2(L+l)·h A =2(lL+hL V= l·L·h d
- 13. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 51 baza poligon regulat): ei) 2Ab (Ab=aria bazei) = Ab·h risma triunghiularÄ regulatÄ: risma patrulatarÄ regulatÄ: risma hexagonalÄ regulatÄ: tetraedrul regulat (toa unt congruente) -prisma regulatÄ (prisma dreaptÄ cu Alat =PB ·h (PB= perimetrul baz Atot = Alat + V P P P - te muchiile s 3 = , ap= 6l h 2 , A =l23l 3 , V= 12 23 l
- 14. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 52 gulatÄ (are baza poligon regulat, iar piciorul perpendicularei din vÃĒrf este centrul-piramida re bazei) Alat = 2 (a pb aP â p=apotema piramidei) 2 ab =apotema bazei) Atot=Ab+Alat ap = (h2 +ab 2 V = 3 iramidÄ triunghiularÄ regulatÄ PiramidÄ patrulaterÄ regulatÄ iramidÄ hexagonalÄ regulatÄ hAb â P P
- 15. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 53 -trunchiul de piramidÄ (regulatÄ) Alat= 2 )( pbB aPP â + (PB=perimetrul bazei mari, Pb =perimetrul bazei mici) Atot =AB +Ab +Alat V = (h â ++ )bBbB AAAA 3 (AB =aria bazei mari, Ab =aria bazei mici) ap 2 =h2 +(aB-ab)2 (aB=apotema bazei mari, ab = apotema bazei mici) Trunchi de piramidÄ triunghiularÄ regulatÄ Trunchi de piramidÄ patrulaterÄ regulatÄ
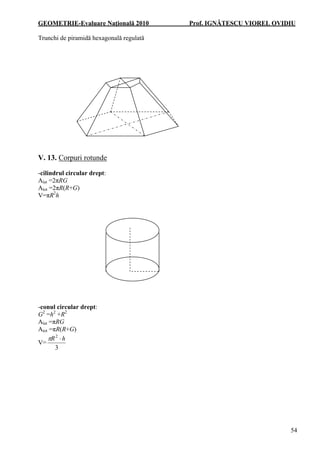
- 16. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 54 Trunchi de piramidÄ hexagonalÄ regulatÄ V. 13. Corpuri rotunde -cilindrul circular drept: Alat =2ÏRG Atot =2ÏR(R+G) V=ÏR2 h -conul circular drept: G2 =h2 +R2 Alat =ÏRG Atot =ÏR(R+G) V= 3 2 hR â Ï
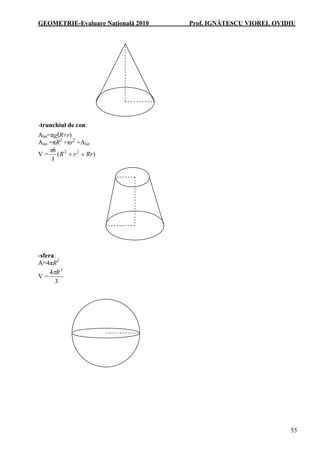
- 17. GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU 55 -trunchiul de con: Alat=Ïg(R+r) Atot =ÏR2 +Ïr2 +Alat V = )( 3 RrrR ++ 22hÏ -sfera: A=4ÏR2 V = 3 4 3 RÏ




![GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU
42
Bisectoarea unui unghi propriu este semidreapta cu originea ÃŪn vÃĒrful unghiului, situatÄ ÃŪn
interiorul acestuia, care formeazÄ cu laturile unghiului iniÅĢial douÄ unghiuri congruente.
DouÄ unghiuri se numesc suplementare dacÄ suma mÄsurilor lor este de 1800
. DouÄ
unghiuri se numesc complementare dacÄ suma mÄsurilor lor este de 900
.
Ex. Suplementul unghiului de 750
29â17ââ este
1800
-750
29â17ââ=1790
59â60ââ-750
29â17ââ=1040
30â43ââ
Complementul sÄu este
900
-750
29â17ââ=890
59â60ââ-750
29â17ââ=140
30â43ââ
DouÄ unghiuri cu acelaÅi vÃĒrf care au laturile unuia ÃŪn prelungirea laturilor celuilalt se
numesc unghiuri opuse la vÃĒrf. DouÄ unghiuri opuse la vÃĒrf sunt congruente. Suma mÄsurilor
unghiurilor formate ÃŪn jurul unui punct este de 3600
.
V. 4. CongruenÅĢa triunghiurilor ; perpendicularitate ÃŪn plan ; paralelism
Figura geometricÄ formatÄ din cele trei segmente determinate de trei puncte necoliniare se
numeÅte triunghi. Suma lungimilor laturilor unui triunghi se numeÅte perimetrul triunghiului (P),
iar jumÄtatea acestuia este semiperimetrul (p). DupÄ laturi triunghiul poate fi: scalen (laturile au
mÄsuri diferite), isoscel (douÄ laturi sunt congruente), echilateral (toate laturile sunt congruente).
DupÄ unghiuri triunghiul poate fi: ascuÅĢitunghic (toate unghiurile sunt ascuÅĢite), dreptunghic (un
unghi este drept), obtuzunghic (un unghi este obtuz). Suma mÄsurilor unghiurilor ÃŪn orice triunghi
este de 1800
. Unghiul care este adiacent Åi suplementar cu un unghi al unui triunghi se numeÅte
unghi exterior al triunghiului.
DouÄ triunghiuri sunt congruente dacÄ laturile triunghiurilor sunt respectiv congruente Åi
unghiurile sunt respectiv congruente. Cazurile de congruenÅĢÄ pentru triunghiuri oarecare:
-L.U.L. (laturÄ-unghi-laturÄ)
-U.L.U. (unghi-laturÄ-unghi)
-L.L.L. (laturÄ-laturÄ-laturÄ)
DatoritÄ criteriului 2 Åi faptului cÄ suma mÄsurilor unghiurilor ÃŪn triunghi este 1800
, se poate enunÅĢa
-L.U.U. (laturÄ-unghi-unghi)
Metoda triunghiurilor congruente ajutÄ la demonstrarea congruenÅĢei a douÄ laturi sau
douÄ unghiuri pe care trebuie sÄ le ÃŪncadram ÃŪn triunghiri despre care se va arÄta cÄ sunt congruente
(conform unuia din cazurile de congruenÅĢÄ).
Ex. Ãn figura urmÄtoare âĒABC âĄâĒDCB Åi âĒACB ⥠âĒDBC. DemonstrÄm cÄ âĒBAC âĄâĒBDC Åi
[AC]⥠[BD].](https://image.slidesharecdn.com/formulegeometrie-160813235339/85/Formule-geometrie-4-320.jpg)
![GEOMETRIE-Evaluare NaÅĢionalÄ 2010 Prof. IGNÄTESCU VIOREL OVIDIU
43
Privim ÎABC Åi ÎDCB. Avem âĒACB ⥠âĒDBC (ipotezÄ), [BC]âĄ[BC] (lat. comunÄ) Åi âĒABC
âĄâĒDCB (ipotezÄ) â(conform U.L.U.) ÎABC ⥠ÎDCB ââĒBAC âĄâĒBDC Åi
[AC]⥠[BD].
DouÄ drepte concurente sunt perpendiculare dacÄ unul din unghiurile ce se formeazÄ ÃŪn
jurul punctului lor comun este unghi drept (d âĨ g).
Fiind dat un punct A exterior dreptei d, atunci punctul B â d a. ÃŪ. AB âĨ d se numeÅte
piciorul perpendicularei din A pe d.
DistanÅĢa de la un punct exterior unei drepte la dreaptÄ este distanÅĢa dintre punct Åi piciorul
perpendicularei duse din acel punct pe dreaptÄ d( A, d) = AB.
Criteriile de congruenÅĢÄ ale triunghiurilor dreptunghice :
-C. C. (catetÄ-catetÄ)
-C. U. ( catetÄ-unghi)
-I. U. (ipotenuzÄ-unghi)
I. C. (ipotenuzÄ-catetÄ)
Proprietatea bisectoarei : un punct din interiorul unui unghi propriu aparÅĢine bisectoarei
unghiului dacÄ Åi numai dacÄ
DistanÅĢele de la punct la laturile unghiului sunt egale.
ConcurenÅĢa bisectoarelor ÃŪntr-un triunghi : ÃŪn orice triunghi cele trei bisectoare sunt
concurente ( punctul lor de intersecÅĢie este centrul cercului ÃŪnscris ÃŪn triunghi).
Mediatoarea unui segment este dreapta perpendicularÄ pe segment ÃŪn mijlocul acestuia.
Proprietatea mediatoarei : un punct aparÅĢine mediatoarei unui segment dacÄ Åi numai dacÄ
are distanÅĢele egale faÅĢÄ de extremitÄÅĢile segmentului.
ConcurenÅĢa mediatoarelor : ÃŪn orice triunghi mediatoarele celor trei laturi sunt concurente
( punctul lor de intersecÅĢie este centrul cercului circumscris triunghiului).
DouÄ drepte sunt paralele dacÄ sunt coplanare Åi nu au nici un punct comun.
Axioma paralelelor (Euclid) : printr-un punct exterior unei drepte date, trece o singurÄ
paralelÄ la dreapta datÄ.
DouÄ drepte intersectate cu o secantÄ formeazÄ o pereche de unghiuri alterne interne
congruente, dacÄ Åi numai dacÄ dreptele sunt paralele.](https://image.slidesharecdn.com/formulegeometrie-160813235339/85/Formule-geometrie-5-320.jpg)