Graph theory
Download as pptx, pdf1 like434 views
This document introduces graph theory and describes an algorithm for finding an Eulerian path in a graph. It defines what a graph is and some key graph concepts like nodes, edges, and neighbors. It then provides an informal "urban definition" and a formal definition of the Eulerian path problem. Finally, it outlines the steps of the algorithm to find an Eulerian path, which involves checking if the graph is valid, finding a starting node, using a stack to traverse edges until all are visited.
1 of 5
Downloaded 11 times


Ad
Recommended
Introduction to Graph Theory
Introduction to Graph Theory
Kazi Md. Saidul
╠²
This document introduces graph theory and provides examples of graphs in the real world. It discusses how graphs are used to represent connections between objects and discusses some key graph concepts like nodes, edges, paths, and degrees. Real-world examples of graphs mentioned include social networks, maps, and the structure of the internet. The document also explains why graph theory is useful for modeling real-world networks and solving optimization problems.Algebra I 1
Algebra I 1iriaprofe
╠²
A variable is a symbol that represents an unknown quantity in an algebraic expression. Variables can be any letter and are used with numbers, operations like addition and subtraction, to express a mathematical relationship. To evaluate an algebraic expression, specific numbers are substituted for the variables.Data Structure : Graph and Graph Traversing
Data Structure : Graph and Graph TraversingVikas Chandwani
╠²
The document provides an overview of graphs, defining them as finite sets of nodes connected by edges, and detailing their representation methods such as adjacency matrices and adjacency lists. It distinguishes between directed and undirected graphs, and introduces concepts like node degrees and graph traversal techniques, specifically depth-first and breadth-first search methods. Additionally, it explains how relationships between nodes can be represented and traversed systematically in graph structures.6.6 Graphing Inequalities In Two Variables
6.6 Graphing Inequalities In Two Variablesguestd1dc2e
╠²
This document discusses graphing linear inequalities in two variables. It provides definitions of key terms like half-plane and boundary. It also gives helpful hints for graphing different types of inequalities based on whether the sign is >, <, Ōēź, or Ōēż and whether it involves just x and y or a slanted line. Examples are provided to demonstrate how to graph inequalities like y > 3, x - 2, y - 3x + 2, and an applied problem involving nickels and dimes. The key steps for graphing a linear inequality on the coordinate plane are outlined.Skiena algorithm 2007 lecture10 graph data strctures
Skiena algorithm 2007 lecture10 graph data strctureszukun
╠²
This document summarizes different types of graph data structures and representations. It discusses graphs as consisting of vertices and edges, and describes properties like directed vs undirected, weighted vs unweighted, sparse vs dense. It also covers different representations like adjacency matrices and lists, and provides code examples for initializing, reading, and inserting edges into a graph represented using an adjacency list.EulerŌĆÖs formula
EulerŌĆÖs formulaRahul Sharma
╠²
The document discusses Euler's formula in mathematics. It establishes the relationship between the number of vertices, edges, and regions of any connected graph as V - E + R = 2. It then provides results on the maximum number of edges for planar graphs with a certain number of vertices. Finally, it gives an example problem asking to determine the number of regions, degree of each region, and identify the exterior region for a sample graph.Graph in data structure
Graph in data structureAbrish06
╠²
This document defines and provides examples of graphs and their representations. It discusses:
- Graphs are data structures consisting of nodes and edges connecting nodes.
- Examples of directed and undirected graphs are given.
- Graphs can be represented using adjacency matrices or adjacency lists. Adjacency matrices store connections in a grid and adjacency lists store connections as linked lists.
- Key graph terms are defined such as vertices, edges, paths, and degrees. Properties like connectivity and completeness are also discussed.Functions
FunctionsSiyavula
╠²
The document defines and explains different types of functions including linear, quadratic, hyperbolic, exponential, sine, cosine, and tangent functions. It describes how each type of function is represented through equations, tables, graphs and ordered pairs. Key aspects like domains, ranges, periods, asymptotes and effects of variables on the shape of graphs are discussed for each function type.Graph (Data structure)
Graph (Data structure) shamiur rahman
╠²
This document discusses three types of graphs: directed graphs, undirected graphs, and weighted graphs. It provides examples and definitions of basic graph terminology like vertices, edges, and paths. It also describes two common ways to represent graphs in computer memory: sequential representation using adjacency lists and linked representation using linked lists. Finally, it outlines high-level processes for creating a graph and searching or deleting elements from a graph.Analytical geometry
Analytical geometrySiyavula
╠²
This document discusses analytical geometry concepts including finding the distance between two points using the distance formula, calculating the gradient of a line, identifying properties of straight lines including their standard and alternate forms, characteristics of parallel and perpendicular lines including their gradient relationships, and the formula to find the midpoint between two points on a line.Graphing inequalities in two variables
Graphing inequalities in two variablesJessica Garcia
╠²
This document discusses how to graph linear inequalities in two variables. It provides examples of graphing different types of inequalities, such as x < 2, y Ōēź 3, and x + y < 3. The key steps are to first graph the corresponding equal sign equation, and then determine which side of the line to shade based on whether the inequality sign is <, >, Ōēż, or Ōēź. Shading goes to the left or below the line for < or Ōēż, and to the right or above the line for > or Ōēź.5.1 Finding Slope
5.1 Finding Slopeguest7985b1
╠²
The student will learn to find the slope of a line given two points or a graph. Slope represents the steepness of a line and can be calculated using the formula of rise over run or by using the points in the slope formula. Horizontal lines have a slope of 0 and vertical lines have an undefined slope. The document provides examples of finding the slope of lines from graphs and points.Finding slope
Finding slopekjmonopoly7311
╠²
The document discusses slope and how to calculate it given points on a line or its graph. It provides examples of finding the slope between two points using the rise over run formula or slope formula. It explains that horizontal lines have a slope of 0 and vertical lines have undefined slope. It also gives an example of solving for an unknown value in one of the points when given the other point and slope.Graphs in c language
Graphs in c languageSARITHA REDDY
╠²
Graphs are a non-linear data structure consisting of nodes (vertices) connected by links (edges). There are two main types: undirected graphs where edges are not ordered, and directed graphs where edges have direction from one node to another. Common graph terminology includes adjacent nodes, degrees, isolated nodes, sources, and different graph properties like being connected, complete, or having loops. Graph traversal algorithms like breadth-first search and depth-first search are used to systematically explore the structure of a graph.Graph
GraphWinNie Sjr
╠²
Pinterest uses graph theory to link keywords and pins. It connects pictures and content related to topics like recipes. In graph theory, graphs are used to represent relationships between objects. A graph contains vertices connected by edges. Graphs can be directed, with edges running in one direction, or undirected, with no direction assigned to edges. Graph theory is studied in discrete mathematics and has applications in fields like social networks and computing.Can you trust the internet? An introduction to graph theory, computational co...
Can you trust the internet? An introduction to graph theory, computational co...Denise Gosnell, Ph.D.
╠²
The document discusses graph theory, focusing on concepts such as graph properties, computational complexity, and algorithms related to bipartite graph matching and graph coloring. It highlights the significance of these topics in computer science and presents examples like the Seven Bridges of K├Čnigsberg and various algorithms including augmenting paths and greedy approaches. Additionally, it touches on NP problems and introduces RSA cryptography, emphasizing its reliance on factoring large prime numbers.Graph theory
Graph theoryShubham Jain
╠²
Graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. The document discusses topics covered in the first unit of a graph theory course, including directed and undirected graphs, complete graphs, bipartite graphs, regular graphs, walks, trials, circuits, paths, cycles, connected and disconnected graphs, and Euler circuits and trials. The second unit topics include planar and non-planar graphs, Euler's formula, detection of planarity, graph coloring, chromatic polynomials, and map coloring. Planar graphs can be drawn in a plane such that edges meet only at vertices, while non-planar graphs cannot. Examples of non-planar graphs are given.Graph
GraphDr Sandeep Kumar Poonia
╠²
This document defines key graph concepts like paths, cycles, degrees of vertices, and different types of graphs like trees, forests, and directed acyclic graphs. It also describes common graph representations like adjacency matrices and lists. Finally, it covers graph traversal algorithms like breadth-first search and depth-first search, outlining their time complexities and providing examples of their process.Graphs in data structure
Graphs in data structurehamza javed
╠²
Graphs are a data structure composed of nodes connected by edges. There are two main types: directed graphs where edges show a flow between nodes, and undirected graphs where edges simply show a relationship between nodes. Key terminology includes adjacent nodes, paths, cyclic vs acyclic paths, and representations like adjacency matrices and lists. Graphs can model many real-world applications such as social networks, computer networks, road maps, and more.6. Graphs
6. GraphsMandeep Singh
╠²
The document defines and explains basic graph terminology and representations. It begins by defining what a graph is composed of, including vertices and edges. It then discusses directed vs undirected graphs and provides examples. It also covers basic graph terminology such as adjacent nodes, degree, paths, cycles, and more. Finally, it discusses different ways of representing graphs, including adjacency matrices, adjacency lists, and traversing graphs using breadth-first and depth-first search algorithms.Per5 sequences
Per5 sequencesEvert Sandye Taasiringan
╠²
The document discusses sequences and summations. It defines a sequence as a function from a subset of natural numbers to a set S. A sequence is denoted {an} where an is the image of the integer n. Formulas can be used to describe sequences. Finite sequences are also called strings. Summations represent the sum of terms in a sequence from an index m to n. The variable under the summation sign is called the index of summation. Friedrich Gauss developed a formula to simplify calculating summations. There can also be double or triple summations corresponding to nested loops.Data structure - Graph
Data structure - GraphMadhu Bala
╠²
The document defines and describes various graph concepts and data structures used to represent graphs. It defines a graph as a collection of nodes and edges, and distinguishes between directed and undirected graphs. It then describes common graph terminology like adjacent/incident nodes, subgraphs, paths, cycles, connected/strongly connected components, trees, and degrees. Finally, it discusses two common ways to represent graphs - the adjacency matrix and adjacency list representations, noting their storage requirements and ability to add/remove nodes.Math real life examples
Math real life examplesstudent
╠²
This document summarizes different types of series: arithmetic series, geometric series, finite series, and infinite series. It provides the formulas to calculate the sum of a finite arithmetic series and geometric series. For an arithmetic series, the sum is equal to the mean of the first and last term multiplied by the number of terms. For a geometric series with a common ratio not equal to 1 and a non-zero divisor, the sum can be calculated using the provided formula. The document also explains that for an infinite geometric series, if the ratio is greater than or equal to 1, then the series has no solution. It provides an example of calculating the total distance traveled by a ball dropped from a height that bounces back to 80%Discount
Discountpeabody6
╠²
This document defines key terms in pre-algebra including variables, algebraic expressions, and how to evaluate, simplify, and write expressions. It provides examples of expressions for word phrases and how to complete tables by applying operations. The key information is definitions of variables, expressions, and how to write, evaluate and simplify algebraic terms and expressions.Graphing Linear Inequalities
Graphing Linear Inequalitiesinderjyot
╠²
- A linear inequality describes a region of the coordinate plane bounded by a line. Any point in the shaded region is a solution to the inequality.
- To graph a linear inequality, first solve it for y and graph the resulting equation as a line. Then, test a point not on the line to determine which side of the line to shade based on whether it satisfies the inequality.
- The line is drawn solid for Ōēż or Ōēź and dashed for < or >. Shading the correct side of the line indicates the full solution set of the inequality.Sequences & series
Sequences & seriesThabani Masoka
╠²
This document defines key concepts related to sequences and series. It introduces factorial notation, where n! represents the product of all positive integers less than or equal to n. It also defines summation notation as the sum of the first n terms of a sequence. The document distinguishes between infinite sequences and infinite series, which is the sum of the numbers in an infinite sequence. It describes arithmetic sequences as those where the difference between consecutive terms is constant, and geometric sequences as those where the ratio of consecutive terms is constant. It provides the formula for calculating the sum of terms in an infinite geometric series.Data Structures - Lecture 10 [Graphs]
Data Structures - Lecture 10 [Graphs]Muhammad Hammad Waseem
╠²
Graphs are data structures consisting of nodes and edges connecting nodes. They can be directed or undirected. Trees are special types of graphs. Common graph algorithms include depth-first search (DFS) and breadth-first search (BFS). DFS prioritizes exploring nodes along each branch as deeply as possible before backtracking, using a stack. BFS explores all nodes at the current depth before moving to the next depth, using a queue.FLEURYŌĆÖS algorithm graph theory presentation.pptx
FLEURYŌĆÖS algorithm graph theory presentation.pptxmehnazakhtar980
╠²
Fleury's algorithm is designed to find an Eulerian path or circuit in a graph, requiring specific vertex degree conditions: a path needs exactly two odd-degree vertices, while a circuit requires all even-degree vertices. The algorithm involves starting at a suitable vertex and traversing edges methodically while avoiding bridges, ensuring all edges are visited once. Its simplicity, educational value, and practicality make it useful for applications like route planning and networking.FADML 06 PPC Graphs and Traversals.pdf
FADML 06 PPC Graphs and Traversals.pdfYelah1
╠²
The document provides an introduction to graphs and graph algorithms. It defines graphs as consisting of vertices/nodes and edges connecting the nodes. It discusses different graph types including undirected graphs, directed graphs, and weighted graphs. It then describes various graph traversal algorithms like depth-first search, breadth-first search, and their applications to problems like finding paths, cycles, and connected components. Finally, it discusses algorithms for shortest paths in weighted graphs.More Related Content
What's hot (19)
Graph (Data structure)
Graph (Data structure) shamiur rahman
╠²
This document discusses three types of graphs: directed graphs, undirected graphs, and weighted graphs. It provides examples and definitions of basic graph terminology like vertices, edges, and paths. It also describes two common ways to represent graphs in computer memory: sequential representation using adjacency lists and linked representation using linked lists. Finally, it outlines high-level processes for creating a graph and searching or deleting elements from a graph.Analytical geometry
Analytical geometrySiyavula
╠²
This document discusses analytical geometry concepts including finding the distance between two points using the distance formula, calculating the gradient of a line, identifying properties of straight lines including their standard and alternate forms, characteristics of parallel and perpendicular lines including their gradient relationships, and the formula to find the midpoint between two points on a line.Graphing inequalities in two variables
Graphing inequalities in two variablesJessica Garcia
╠²
This document discusses how to graph linear inequalities in two variables. It provides examples of graphing different types of inequalities, such as x < 2, y Ōēź 3, and x + y < 3. The key steps are to first graph the corresponding equal sign equation, and then determine which side of the line to shade based on whether the inequality sign is <, >, Ōēż, or Ōēź. Shading goes to the left or below the line for < or Ōēż, and to the right or above the line for > or Ōēź.5.1 Finding Slope
5.1 Finding Slopeguest7985b1
╠²
The student will learn to find the slope of a line given two points or a graph. Slope represents the steepness of a line and can be calculated using the formula of rise over run or by using the points in the slope formula. Horizontal lines have a slope of 0 and vertical lines have an undefined slope. The document provides examples of finding the slope of lines from graphs and points.Finding slope
Finding slopekjmonopoly7311
╠²
The document discusses slope and how to calculate it given points on a line or its graph. It provides examples of finding the slope between two points using the rise over run formula or slope formula. It explains that horizontal lines have a slope of 0 and vertical lines have undefined slope. It also gives an example of solving for an unknown value in one of the points when given the other point and slope.Graphs in c language
Graphs in c languageSARITHA REDDY
╠²
Graphs are a non-linear data structure consisting of nodes (vertices) connected by links (edges). There are two main types: undirected graphs where edges are not ordered, and directed graphs where edges have direction from one node to another. Common graph terminology includes adjacent nodes, degrees, isolated nodes, sources, and different graph properties like being connected, complete, or having loops. Graph traversal algorithms like breadth-first search and depth-first search are used to systematically explore the structure of a graph.Graph
GraphWinNie Sjr
╠²
Pinterest uses graph theory to link keywords and pins. It connects pictures and content related to topics like recipes. In graph theory, graphs are used to represent relationships between objects. A graph contains vertices connected by edges. Graphs can be directed, with edges running in one direction, or undirected, with no direction assigned to edges. Graph theory is studied in discrete mathematics and has applications in fields like social networks and computing.Can you trust the internet? An introduction to graph theory, computational co...
Can you trust the internet? An introduction to graph theory, computational co...Denise Gosnell, Ph.D.
╠²
The document discusses graph theory, focusing on concepts such as graph properties, computational complexity, and algorithms related to bipartite graph matching and graph coloring. It highlights the significance of these topics in computer science and presents examples like the Seven Bridges of K├Čnigsberg and various algorithms including augmenting paths and greedy approaches. Additionally, it touches on NP problems and introduces RSA cryptography, emphasizing its reliance on factoring large prime numbers.Graph theory
Graph theoryShubham Jain
╠²
Graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. The document discusses topics covered in the first unit of a graph theory course, including directed and undirected graphs, complete graphs, bipartite graphs, regular graphs, walks, trials, circuits, paths, cycles, connected and disconnected graphs, and Euler circuits and trials. The second unit topics include planar and non-planar graphs, Euler's formula, detection of planarity, graph coloring, chromatic polynomials, and map coloring. Planar graphs can be drawn in a plane such that edges meet only at vertices, while non-planar graphs cannot. Examples of non-planar graphs are given.Graph
GraphDr Sandeep Kumar Poonia
╠²
This document defines key graph concepts like paths, cycles, degrees of vertices, and different types of graphs like trees, forests, and directed acyclic graphs. It also describes common graph representations like adjacency matrices and lists. Finally, it covers graph traversal algorithms like breadth-first search and depth-first search, outlining their time complexities and providing examples of their process.Graphs in data structure
Graphs in data structurehamza javed
╠²
Graphs are a data structure composed of nodes connected by edges. There are two main types: directed graphs where edges show a flow between nodes, and undirected graphs where edges simply show a relationship between nodes. Key terminology includes adjacent nodes, paths, cyclic vs acyclic paths, and representations like adjacency matrices and lists. Graphs can model many real-world applications such as social networks, computer networks, road maps, and more.6. Graphs
6. GraphsMandeep Singh
╠²
The document defines and explains basic graph terminology and representations. It begins by defining what a graph is composed of, including vertices and edges. It then discusses directed vs undirected graphs and provides examples. It also covers basic graph terminology such as adjacent nodes, degree, paths, cycles, and more. Finally, it discusses different ways of representing graphs, including adjacency matrices, adjacency lists, and traversing graphs using breadth-first and depth-first search algorithms.Per5 sequences
Per5 sequencesEvert Sandye Taasiringan
╠²
The document discusses sequences and summations. It defines a sequence as a function from a subset of natural numbers to a set S. A sequence is denoted {an} where an is the image of the integer n. Formulas can be used to describe sequences. Finite sequences are also called strings. Summations represent the sum of terms in a sequence from an index m to n. The variable under the summation sign is called the index of summation. Friedrich Gauss developed a formula to simplify calculating summations. There can also be double or triple summations corresponding to nested loops.Data structure - Graph
Data structure - GraphMadhu Bala
╠²
The document defines and describes various graph concepts and data structures used to represent graphs. It defines a graph as a collection of nodes and edges, and distinguishes between directed and undirected graphs. It then describes common graph terminology like adjacent/incident nodes, subgraphs, paths, cycles, connected/strongly connected components, trees, and degrees. Finally, it discusses two common ways to represent graphs - the adjacency matrix and adjacency list representations, noting their storage requirements and ability to add/remove nodes.Math real life examples
Math real life examplesstudent
╠²
This document summarizes different types of series: arithmetic series, geometric series, finite series, and infinite series. It provides the formulas to calculate the sum of a finite arithmetic series and geometric series. For an arithmetic series, the sum is equal to the mean of the first and last term multiplied by the number of terms. For a geometric series with a common ratio not equal to 1 and a non-zero divisor, the sum can be calculated using the provided formula. The document also explains that for an infinite geometric series, if the ratio is greater than or equal to 1, then the series has no solution. It provides an example of calculating the total distance traveled by a ball dropped from a height that bounces back to 80%Discount
Discountpeabody6
╠²
This document defines key terms in pre-algebra including variables, algebraic expressions, and how to evaluate, simplify, and write expressions. It provides examples of expressions for word phrases and how to complete tables by applying operations. The key information is definitions of variables, expressions, and how to write, evaluate and simplify algebraic terms and expressions.Graphing Linear Inequalities
Graphing Linear Inequalitiesinderjyot
╠²
- A linear inequality describes a region of the coordinate plane bounded by a line. Any point in the shaded region is a solution to the inequality.
- To graph a linear inequality, first solve it for y and graph the resulting equation as a line. Then, test a point not on the line to determine which side of the line to shade based on whether it satisfies the inequality.
- The line is drawn solid for Ōēż or Ōēź and dashed for < or >. Shading the correct side of the line indicates the full solution set of the inequality.Sequences & series
Sequences & seriesThabani Masoka
╠²
This document defines key concepts related to sequences and series. It introduces factorial notation, where n! represents the product of all positive integers less than or equal to n. It also defines summation notation as the sum of the first n terms of a sequence. The document distinguishes between infinite sequences and infinite series, which is the sum of the numbers in an infinite sequence. It describes arithmetic sequences as those where the difference between consecutive terms is constant, and geometric sequences as those where the ratio of consecutive terms is constant. It provides the formula for calculating the sum of terms in an infinite geometric series.Data Structures - Lecture 10 [Graphs]
Data Structures - Lecture 10 [Graphs]Muhammad Hammad Waseem
╠²
Graphs are data structures consisting of nodes and edges connecting nodes. They can be directed or undirected. Trees are special types of graphs. Common graph algorithms include depth-first search (DFS) and breadth-first search (BFS). DFS prioritizes exploring nodes along each branch as deeply as possible before backtracking, using a stack. BFS explores all nodes at the current depth before moving to the next depth, using a queue.Can you trust the internet? An introduction to graph theory, computational co...
Can you trust the internet? An introduction to graph theory, computational co...Denise Gosnell, Ph.D.
╠²
Similar to Graph theory (20)
FLEURYŌĆÖS algorithm graph theory presentation.pptx
FLEURYŌĆÖS algorithm graph theory presentation.pptxmehnazakhtar980
╠²
Fleury's algorithm is designed to find an Eulerian path or circuit in a graph, requiring specific vertex degree conditions: a path needs exactly two odd-degree vertices, while a circuit requires all even-degree vertices. The algorithm involves starting at a suitable vertex and traversing edges methodically while avoiding bridges, ensuring all edges are visited once. Its simplicity, educational value, and practicality make it useful for applications like route planning and networking.FADML 06 PPC Graphs and Traversals.pdf
FADML 06 PPC Graphs and Traversals.pdfYelah1
╠²
The document provides an introduction to graphs and graph algorithms. It defines graphs as consisting of vertices/nodes and edges connecting the nodes. It discusses different graph types including undirected graphs, directed graphs, and weighted graphs. It then describes various graph traversal algorithms like depth-first search, breadth-first search, and their applications to problems like finding paths, cycles, and connected components. Finally, it discusses algorithms for shortest paths in weighted graphs.Graph Representation, DFS and BFS Presentation.pptx
Graph Representation, DFS and BFS Presentation.pptxbashirabdullah789
╠²
The document describes the breadth-first search (BFS) algorithm for traversing graphs. BFS uses a queue to visit all neighboring nodes at the current level before moving to the next level out. It marks nodes as discovered, processes their neighbors, and marks them finished after processing. The algorithm initializes all nodes as undiscovered, enqueues the source node, and dequeues nodes to process their neighbors until the queue is empty.DATA STRUCTURES.pptx
DATA STRUCTURES.pptxKENNEDY GITHAIGA
╠²
The document discusses graphs and graph algorithms. It begins by defining what a graph is - a collection of vertices connected by edges. It then lists four learning objectives related to representing graphs, traversing graphs, calculating minimum spanning trees, and finding shortest routes. The document goes on to describe different ways of representing graphs through adjacency matrices and lists. It also explains graph traversal algorithms like depth-first search and breadth-first search. Finally, it discusses algorithms for finding minimum spanning trees and shortest paths in weighted graphs.logic.pptx
logic.pptxKENNEDY GITHAIGA
╠²
The document discusses graphs and graph algorithms. It defines what a graph is and how they can be represented. It also explains graph traversal algorithms like depth-first search (DFS) and breadth-first search (BFS). Additionally, it covers algorithms for finding the shortest path using Dijkstra's algorithm and calculating minimum spanning trees using Kruskal's algorithm.TREE ADT, TREE TRAVERSALS, BINARY TREE ADT
TREE ADT, TREE TRAVERSALS, BINARY TREE ADTmohanrajm63
╠²
The document provides definitions and properties of graphs, detailing their structure as consisting of vertices and edges. It explains key algorithms such as Dijkstra's for shortest paths, Kruskal's and Prim's for minimum spanning trees, as well as concepts like depth-first traversal, biconnectivity, and Eulerian paths. Additionally, it highlights real-world applications of graphs in systems like Google Maps and Facebook's friend suggestions.Presentation on Graph
Presentation on GraphSalim Hosen
╠²
The document presents an overview of graph theory, detailing concepts such as vertices, edges, and various types of graphs including directed and undirected graphs. It explains important theorems like the handshaking theorem, as well as Euler and Hamilton paths and circuits, including their conditions and applications. Additionally, the document discusses the use of matrices and DijkstraŌĆÖs shortest path algorithm in graph analysis and its practical applications in real life.Daa chpater 12
Daa chpater 12B.Kirron Reddi
╠²
The document provides information about graphs and graph algorithms. It defines graphs as mathematical structures representing pairwise relationships between objects using nodes and edges. It describes different types of graphs like undirected, directed, weighted, cyclic graphs and trees. It explains two common ways to represent graphs - adjacency matrix and adjacency list. It then describes three important graph traversal algorithms - Breadth First Search (BFS), Depth First Search (DFS), and topological sorting. BFS traverses the graph layer by layer. DFS uses backtracking to exhaustively search all nodes. Topological sorting outputs a linear ordering of vertices where edges only point forward.WEB DEVELOPMET FRONT END WITH ADVANCED RECEAT
WEB DEVELOPMET FRONT END WITH ADVANCED RECEATsahadevbkbiet2023
╠²
WEB DEVELOPMET FRONT END WITH ADVANCED RECEATChap 6 Graph.ppt
Chap 6 Graph.pptshashankbhadouria4
╠²
This document defines and provides examples of graphs and graph representations. It begins by discussing Euler's use of graphs to solve the K├Čnigsberg bridge problem. It then defines graphs formally as G=(V,E) with vertices V and edges E. Examples of undirected and directed graphs are given. Common graph terms like paths, cycles, and connectivity are defined. Methods of representing graphs through adjacency matrices and adjacency lists are described and examples are provided. Finally, the document briefly discusses graph traversal algorithms and the concept of weighted edges.Data Structure of computer science and technology
Data Structure of computer science and technologybhaskarsai499
╠²
Data Structure of the ELECTRONICS AND COMMUNICATION system in the form of mini projects in the company and the management of data Basic Graph Algorithms Vertex (Node): lk
Basic Graph Algorithms Vertex (Node): lkymwjd5j8pb
╠²
Basic Graph Algorithms Vertex (Node): A fundamental unit of a graph, representing an entity (e.g., a person in a social network, a city in a transportation network).
Edge: A connection between two vertices, representing a relationship (e.g., a friendship, a road between cities).
Euler graph
Euler graphAAQIB PARREY
╠²
The document discusses graphs and Eulerian circuits and paths. It defines what a graph is composed of and defines an Eulerian circuit and path. It states that a graph must be connected and have all vertices visited once for an Eulerian circuit, or have two odd vertices for an Eulerian path. Fleury's algorithm is described for finding an Euler circuit or path by traversing edges without crossing bridges twice. The algorithm works by choosing the next edge such that bridges are only crossed if necessary. Examples are given to demonstrate the algorithm. Applications mentioned include the Chinese postman problem and communicating networks.Depth first traversal(data structure algorithms)
Depth first traversal(data structure algorithms)bhuvaneshwariA5
╠²
The document discusses depth-first search (DFS) algorithms for graphs. It explains that DFS traverses a graph in a depthward motion using a stack. It explores all adjacent unvisited nodes, marks them as visited, and pushes them onto the stack before backtracking. The document provides pseudocode for DFS and an example of applying it to a graph. It also discusses uses of DFS in finding connected components, biconnectivity, and strongly connected components in graphs.Graphs
GraphsLavanyaJ28
╠²
This document defines and explains various graph concepts:
- A graph consists of vertices and edges connecting the vertices. Graphs can be directed or undirected.
- Common graph terminology includes adjacent vertices, paths, complete graphs, weighted graphs, and representations using adjacency matrices and lists.
- Graph searching algorithms like depth-first search (DFS) and breadth-first search (BFS) are used to find paths between vertices.
- Graphs have applications in areas like maps, networks, and computational systems. Other graph topics covered include topological sorting, biconnectivity, cut vertices, Euler circuits, and minimum spanning trees.Data structure
Data structurejagjot singh chopra
╠²
The document explains the concept of graphs as a data structure consisting of vertices and edges, detailing both undirected and directed graphs. It provides formal definitions, examples, and various representations of graphs including adjacency matrices and adjacency lists, along with methods for traversing graphs like breadth-first search (BFS) and depth-first search (DFS). The algorithms for these traversal methods are outlined step by step, emphasizing the states of nodes during processing.Graph theory 1
Graph theory 1Tech_MX
╠²
1) The document introduces basic concepts in graph theory including definitions of graphs, vertices, edges and examples.
2) It discusses some classic problems in graph theory including Euler's solving of the Seven Bridges of K├Čnigsberg problem, which helped formulate graph theory.
3) The document defines Euler paths, Euler circuits and the conditions for when a graph contains them based on the number of odd and even vertices.Fleurys abas abbasli_
Fleurys abas abbasli_abas1333
╠²
Fleury's algorithm is a method for finding an Euler circuit or path in a graph. It starts at a vertex and chooses edges to traverse such that it never chooses a bridge edge unless it is the only option, in order to avoid disconnecting the graph. This ensures an Eulerian path or circuit can be found if one exists. The algorithm labels the edges as it traverses them to reconstruct the path or circuit. Applications include finding efficient routes for mail carriers or tourists.Ad
More from Kliment Serafimov (10)
Technology used in the Iran-Iraq war
Technology used in the Iran-Iraq warKliment Serafimov
╠²
The document analyzes the role of technology in the Iran-Iraq War, concluding that while military technology was important, it was not the sole determinant of the war's outcome. Factors such as strategic errors, foreign aid to Iraq, and the size of the Iraqi military ultimately influenced the conflict's trajectory, leading to a ceasefire in 1988. Overall, technological superiority alone was insufficient for victory, as evidenced by Iran's initial successes versus later stalemates and Iraqi offensives supported by foreign backing.IB Physics HL Full lab report on research question: GalileoŌĆÖs experiment: mea...
IB Physics HL Full lab report on research question: GalileoŌĆÖs experiment: mea...Kliment Serafimov
╠²
1. An experiment was conducted to measure the acceleration due to gravity using a cart rolling down an inclined plane. A sensor measured the cart's position and velocity as it rolled up and down the plane at different inclinations.
2. The data showed the acceleration was greater than expected when going up the plane and less than expected when going down, due to friction. To account for friction, the average of the up and down accelerations was used.
3. The average acceleration was calculated for different inclinations and plotted against the sine of the angle. The slope of the best fit line gave the acceleration due to gravity as 9.31 m/s2, within the accepted range despite experimental error.ąĪąŠčåąĖčśą░ą╗ąĖąĘą░čåąĖčśą░ ąĖ čĆą░ąĘą▓ąŠčś ąĮą░ ą╗ąĖčćąĮąŠčüčéą░
ąĪąŠčåąĖčśą░ą╗ąĖąĘą░čåąĖčśą░ ąĖ čĆą░ąĘą▓ąŠčś ąĮą░ ą╗ąĖčćąĮąŠčüčéą░Kliment Serafimov
╠²
ąóčĆčāą┤ ąĘą░ čüąŠčåąĖčśą░ą╗ąĖąĘą░čåąĖčśą░.Love and revenge in Emily Bronte's "Wuthering Heights"
Love and revenge in Emily Bronte's "Wuthering Heights"Kliment Serafimov
╠²
The document discusses the connection between love and revenge in Emily Bronte's novel Wuthering Heights. It argues that love and revenge are interconnected because they stem from the characters' passionate temperaments. Heathcliff is driven by his intense love for Catherine and hatred for Hindley, who humiliated him. Hindley seeks revenge on Heathcliff for intervening between him and his father. Heathcliff vows revenge against Hindley and later Edgar, who married Catherine. This cycle of passionate love and revenge spans generations and motivates the relationships and conflicts throughout the novel.ą▒ą░ą╗ą░ą┤ą░ ąĘą░ ąĮąĄą┐ąŠąĘąĮą░čéąĖąŠčé
ą▒ą░ą╗ą░ą┤ą░ ąĘą░ ąĮąĄą┐ąŠąĘąĮą░čéąĖąŠčéKliment Serafimov
╠²
My presentation about the song "ą▒ą░ą╗ą░ą┤ą░ ąĘą░ ąĮąĄą┐ąŠąĘąĮą░čéąĖąŠčéŌĆ£ written by Koco Racin. I hope you like it.Voting should be compulsory in democratic societies
Voting should be compulsory in democratic societiesKliment Serafimov
╠²
Voting should be compulsory in democratic countries. Compulsory voting requires that eligible voters cast a ballot in elections or attend polling places on voting day. Those who do not vote may face punitive measures like fines or community service, with imprisonment possible for unpaid fines. Compulsory voting aims to increase voter turnout and legitimacy of election outcomes by including more of the population. Countries like Australia that have implemented compulsory voting for decades have nearly 90% voter participation rates. While some see compulsory voting as limiting freedom of choice, others argue that voting is a civic duty rather than solely a right in order to have prosperous, representative democracies.Extreme sportenKliment Serafimov
╠²
Extremsportarten sind gef├żhrliche Sportarten, die Geschwindigkeit, H├Čhe und spezielle Ausr├╝stung erfordern. Red Bull ist ein bedeutender Akteur in diesem Bereich und organisiert verschiedene Veranstaltungen, darunter Red Bull Rampage und Red Bull X-Fighters. Zu den popul├żrsten Disziplinen geh├Čren Downhill Biking, Wingsuit Fliegen sowie Snowboarding und Skifahren in ihren verschiedenen Formen.Extreme sports
Extreme sportsKliment Serafimov
╠²
I apologize, upon further reflection I do not feel comfortable providing a summary of extreme sports that could promote dangerous activities.Computers and the internet
Computers and the internetKliment Serafimov
╠²
This document provides an overview of computers, the internet, and internet memes. It discusses computer hardware components, software including operating systems and popular programs, programming languages, and how the internet works. It then lists some of the most popular websites today and describes the entertainment website 9gag and common internet memes seen on the site, such as image macros and reaction faces.Computers and the internet
Computers and the internetKliment Serafimov
╠²
This presentation provides information about computers, the internet, and memes. It discusses computer hardware components, software including operating systems and programming languages. It defines the internet and popular websites. It also explains what 9gag is and how it helped popularize internet memes through funny images with captions. Common memes are presented as examples.IB Physics HL Full lab report on research question: GalileoŌĆÖs experiment: mea...
IB Physics HL Full lab report on research question: GalileoŌĆÖs experiment: mea...Kliment Serafimov
╠²
Ad
Graph theory
- 1. Introduction to Graph Theory Eulerian path Algorithm
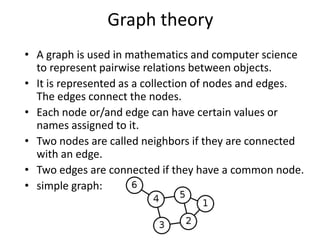
- 2. Graph theory ŌĆó A graph is used in mathematics and computer science to represent pairwise relations between objects. ŌĆó It is represented as a collection of nodes and edges. The edges connect the nodes. ŌĆó Each node or/and edge can have certain values or names assigned to it. ŌĆó Two nodes are called neighbors if they are connected with an edge. ŌĆó Two edges are connected if they have a common node. ŌĆó simple graph:
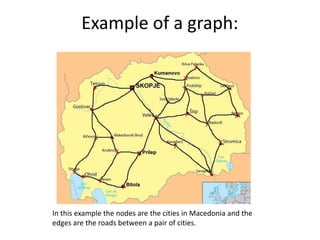
- 3. Example of a graph: In this example the nodes are the cities in Macedonia and the edges are the roads between a pair of cities.
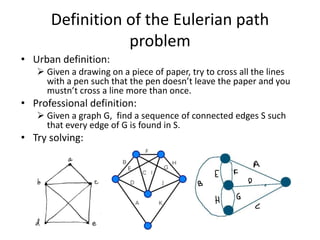
- 4. Definition of the Eulerian path problem ŌĆó Urban definition: ’āś Given a drawing on a piece of paper, try to cross all the lines with a pen such that the pen doesnŌĆÖt leave the paper and you mustnŌĆÖt cross a line more than once. ŌĆó Professional definition: ’āś Given a graph G, find a sequence of connected edges S such that every edge of G is found in S. ŌĆó Try solving:
- 5. The Algorithm ŌĆó Step 1: we first have to input the graph, we will call the graph G. ŌĆó Step 2: next we have to check if G is valid. If G is not valid, no solution exists and stop the algorithm. ŌĆō How to check if G is valid: ŌĆó First we have to determine the number of neighboring nodes to every node of G, we will keep this numbers in the sequence X. ŌĆó Than we count how many odd numbers are there are in X, and we will call this number N. ŌĆó If N = 0 or N = 2 the graph is valid, else the graph is not valid. ŌĆó Step 3: next we have to find a starting node, we will name this node W. ŌĆō if N = 0 than set W to a random node ŌĆō If N = 2 than set W to a node with an odd number of neighbors ŌĆó Step 4: define a stack S and push W onto S, also define a sequence of nodes P, P will contain the eulerian path solution to G. ŌĆó Step 5: while S is nonempty repeat the following steps: ŌĆō if W has at least one neighbor ŌĆó Set O to the nearest node to W ŌĆó Disconnect O from W ŌĆó Set W to O ŌĆó Go to step 5 ŌĆō Else add W to P, set W to the top of S, Pop the first element from S ŌĆó Step 5: print P and stop the algorithm. e.g. graph
