Koordinatni
Download as ppt, pdf0 likes3,872 views
Dokument obja邸njava koordinatni sustav u ravnini, povezujui ureene pare racionalnih brojeva s tokama u toj ravnini. Predstavlja povijest i znaaj Ren辿ho Descartesa, koji je razvio ovaj sustav i njegovu primjenu u matematici i filozofiji. Takoer, ukljuuje primjere odreivanja koordinate toke i zadatke za vje転bu vezane uz crtanje i analizu koordinatnog sustava.
Koordinatni
- 2. KOORDINATNI SUSTAV U RAVNINI
- 3. Danas emo nauiti kako se tokama u ravnini pridru転uju ureeni parovi racionalnih brojeva i obrnuto, kako ureenom paru brojeva pridru転iti toku u ravnini.
- 4. No da bismo to mogli moramo prvo uvesti KOORDINATNI SUSTAV U RAVNINI! Tko li ga je samo smislio?
- 5. Ren辿 Descartes (1561-1626) Matematiar i filozof, zvan jo邸 Cartesius roen je u La Haye (Francuska). Zbog krhkog zdravlja, od djetinjstva nije se dizao iz kreveta prije 11h.
- 6. U matematici je poznat jer je pokazao da se bilo koja algebarska formula mo転e nacrtati kao krivulja u koordinatnom sustavu. To je povezalo algebru razvijenu u arapskom i hindustikom svijetu s geometrijom karakteristinom za grku kulturu. Njegovo mi邸ljenje je bilo da je samo matematika pouzdana dakle sve se mora na njoj bazirati! U filozofiji je poznat i po izjavi: Cognito, ergo sum ! tj. Mislim, dakle jesam!
- 7. Posljednje godine 転ivota seli se u vedsku gdje je pouavao kraljicu Kristinu od vedske. Ona je 転eljela prouavati matematiku u 5 h ujutro, pa je Descartes morao promijeniti svoje navike o kasnom ustajanju nakon 60 godina. Nakon nekoliko mjeseci vi邸e uope nije ustao. Umro je od upale plua u hladnoj vedskoj!
- 8. Ponovimo najprije brojevni pravac : Na pravcu odaberemo toku O i desno od nje toku E. Toki O pridru転imo broj O, a toki E broj 1 . Toka O zove se ishodi邸te , a toka E jedinina toka . O E 0 1 Ka転emo da smo uveli koordinatni sustav na pravcu.
- 9. ZAPII I PRECRTAJ: y os Ako nacrtamo dvije meusobno okomite os ordinata koordinatne osi sa zajednikim ishodi邸tem O i na svakoj od osi odredimo jedininu du転inu, tada ka転emo da smo uveli KOORDINATNI SUSTAV U 1 RAVNINI. 0 1 x os os apscisa x os i y os nazivamo jo邸 i KOORDINATNE OSI.
- 10. Ponovimo zatim ureeni par : Ureeni par je par brojeva u kojem znamo koji broj je prvi lan para, a koji broj drugi lan para. (x, y)
- 11. Poka転imo sada kako zadanoj toki u ravnini pridru転ujemo ureeni par brojeva.
- 12. PRIMJER 1 Odredi ureeni par brojeva pridru転en danim tokama ravnine.
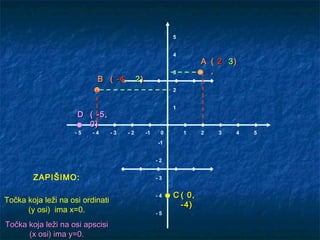
- 13. 5 4 A ( 2 3) 3 , B ( -4 , 2 ) 2 1 D ( -5, 0) -5 -4 -3 -2 -1 0 1 2 3 4 5 -1 -2 ZAPIIMO: -3 -4 C ( 0, Toka koja le転i na osi ordinati -4) (y osi) ima x=0. -5 Toka koja le転i na osi apscisi (x osi) ima y=0.
- 14. Zapi邸i (crveno oznaeno): Ureeni par brojeva (x,y) pridru転en nekoj toki T na nain prikazan u prethodnom primjeru nazivamo jo邸 i KOORDINATE TOKE T. Pi邸emo: T(x, y) apscisa toke T ordinata toke T
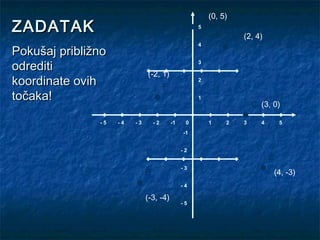
- 15. D (0, 5) ZADATAK 5 A (2, 4) 4 Poku邸aj pribli転no odrediti 3 (-2, 1) koordinate ovih F 2 toaka! 1 C (3, 0) -5 -4 -3 -2 -1 0 1 2 3 4 5 -1 -2 E -3 B (4, -3) -4 (-3, -4) -5
- 16. Poka転imo zatim kako zadanom paru ureenih brojeva pridru転ujemo toku ravnine u koju smo uveli koordinatni sustav.
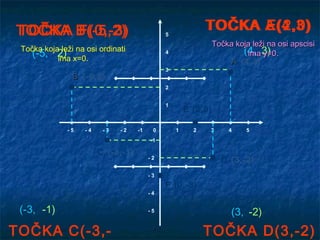
- 17. PRIMJER 2 Nacrtaj u koordinatnoj ravnini toke sa sljedeim koordinatama: A(4, 3), B(-5, 2), C(-3, -1), D(3, -2), E(2, 0) i F(0, -3).
- 18. TOKA B(-5,2) TOKA F(0,-3) 5 TOKA A(4,3) E(2,0) Toka koja le転i na osi apscisi Toka koja le転i na osi ordinati (-5, 2) x=0. 4 (4, 3) ima y=0. ima A (4,3) 3 B (-5,2) 2 1 E (2,0) -5 -4 -3 -2 -1 0 1 2 3 4 5 -1 C (-3,-1) -2 D (3,-2) -3 F (0,-3) -4 (-3, -1) -5 (3, -2) TOKA C(-3,- TOKA D(3,-2)
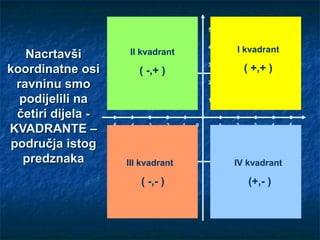
- 19. 5 4 I kvadrant Nacrtav邸i II kvadrant koordinatne osi 3 ( -,+ ) ( +,+ ) ravninu smo 2 podijelili na 1 etiri dijela - KVADRANTE -5 -4 -3 -2 -1 0 -1 1 2 3 4 5 podruja istog -2 predznaka III kvadrant IV kvadrant -3 ( -,- ) -4 (+,- ) -5
- 20. ZADATAK ZA VJE貼BU Nacrtaj u svojoj bilje転nici koordinatni sustav u ravnini pa naznai toke pridru転ene sljedeim ureenim parovima: a) A(2, 5), B(-1, 3), C(-4, -2), D(5, 1), E(3, 0) i F(0, -4). b) A(-4, 5), B(0, 2), C(1, -6), D(3, 4), E(-1, -3) i F(6, 0). Za svaku od toaka navedi u kojem se kvadrantu nalazi.
- 21. VJE貼BA Rije邸ite slijedee zadatke u bilje転nicu: Ud転benik, stranica 28, zadatak 46 stranica 22, zadatak 41 stranica 27, zadatak 43, 44
- 22. Internet nudi: http://apleti.normala.hr S desne strane odabrati KOORDINATNI SUSTAV Odabrati dokument TOKA ZADANA RAZLOMKOM