More Related Content
What's hot (9)
Similar to L'ellisse (20)
More from Student (10)
Recently uploaded (20)
L'ellisse
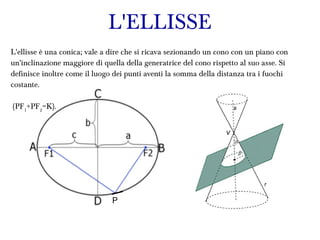
- 1. L'ELLISSE L'ellisse 竪 una conica; vale a dire che si ricava sezionando un cono con un piano con un'inclinazione maggiore di quella della generatrice del cono rispetto al suo asse. Si definisce inoltre come il luogo dei punti aventi la somma della distanza tra i fuochi costante. (PF1 +PF2 =K). P
- 2. Punti notevoli a=Semiasse maggiore b=Semiasse minore c=Semiasse focale 2a=Asse maggiore 2b=Asse minore 2c=Asse focale b2 =a2 -c2 COORDINATE: A, B, C, D = vertici F1 (-c; 0) F2 (c; 0) A (-a; 0) B (a; 0) C (b; 0) D (-b; 0) *Dimostrazione PF1 +PF2 =2a * PF1 = (x+c)2 + y2 a c b
- 3. Eccentricit Definisce quanto un ellisse 竪 schiacciato e si esprime dividendo l'asse focale per quello maggiore, quindi: Il valore dell'eccentricit 竪 sempre compreso tra 0 e 1. Se uguale a 0, i due fuochi coincidono e l'ellisse degenera in una circonferenza di raggio a. Se tende a 1, l'ellisse si schiaccia sempre pi湛 e quando assume precisamente 1 degenera in un segmento lungo 2a percorso due volte,
- 4. Altre caratteristiche notevoli SEMILATO RETTO: Il semilato retto di un'ellisse, definisce la distanza tra ciascuno dei fuochi dell'ellisse e l'ellisse stessa, misurata lungo una linea perpendicolare all'asse maggiore 2a. Si esprime in funzione di a e b, grazie alla formula: AREA: L'area di un ellisse 竪 espressa dalla formula:
- 5. Fuochi sull'asse y Nel caso in cui i fuochi si trovassero sull'asse delle y, a formula dell'ellisse resta invariata e l'unica cosa che cambia 竪 il fatto che in questo caso b corrisponde all'asse maggiore. Ci嘆 si limita ad alterare la formula dell'eccentricit, che diventa: b
- 6. Tangenza 1) METODO DEL DELTA (valido per tutte le coniche) Risolvo il sistema tra l'equazione della circonferenza e della retta e metto il delta della risolvente pari a zero (in modo da avere una sola soluzione). 2) METODO DELLO SDOPPIAMENTO Applico la formula dello sdoppiamento nel caso in cui il punto 竪 sull'ellisse, quindi sostituisco x0 e y0 con le coordinate del punto. y-y0 =m(x-x0 )
- 7. Tangenza 1) METODO DEL DELTA (valido per tutte le coniche) Risolvo il sistema tra l'equazione della circonferenza e della retta e metto il delta della risolvente pari a zero (in modo da avere una sola soluzione). 2) METODO DELLO SDOPPIAMENTO Applico la formula dello sdoppiamento nel caso in cui il punto 竪 sull'ellisse, quindi sostituisco x0 e y0 con le coordinate del punto. y-y0 =m(x-x0 )