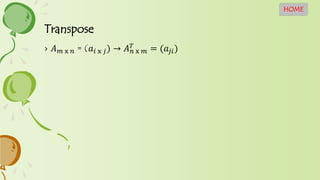�ݺ�ߣ

Oleh :
Apriana Romansyah, S.Pd.
Bab 1.
Matriks

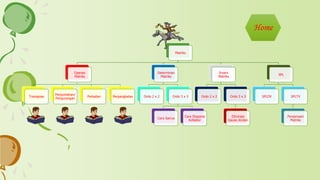
Matriks
Operasi
Matriks
Transpose
Penjumlahan/
Pengurangan
Perkalian Perpangkatan
Determinan
Matriks
Ordo 2 x 2 Ordo 3 x 3
Cara Sarrus
Cara Ekspansi
Kofaktor
Invers
Matriks
Ordo 2 x 2 Ordo 3 x 3
Eliminasi
Gauss-Jordan
SPL
SPLDV SPLTV
Persamaan
Matriks
Home

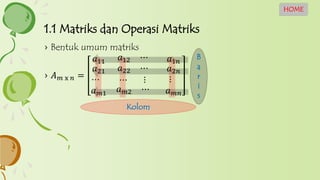
1.1 Matriks dan Operasi Matriks
HOME
› Bentuk umum matriks
› 𝐴 𝑚 x 𝑛 =
𝑎11 𝑎12 ⋯ 𝑎1𝑛
𝑎21
⋯
𝑎22 ⋯
⋯ ⋮
𝑎2𝑛
⋮
𝑎 𝑚1 𝑎 𝑚2 ⋯ 𝑎 𝑚𝑛
Kolom
B
a
r
i
s

Ordo Matriks
Ditulis sebagai banyak baris x banyak kolom
 Kesamaan Matriks
Dua matriks dikatakan sama jika dan hanya jika satu
matriks merupakan duplikat matriks lainnya.
 Transpose Matriks
Transpose matriks 𝐴 𝑚 x 𝑛 merupakan matriks A yang
diubah kedudukan baris menjadi kolom dan ditulis
sebagai AT.
HOME

Transpose
HOME
› 𝐴 𝑚 x 𝑛 = (𝑎𝑖 x 𝑗) → 𝐴 𝑛 x 𝑚
𝑇
= (𝑎𝑗𝑖)

Penjumlahan dan pengurangan matriks
HOME
› Penjumlahan dan pengurangan dua matriks A dan B
dapat dilakukan jika mengikuti aturan berikut.
(i) Ordo (A) = ordo (B)
(ii) A  B = 𝑎𝑖𝑗  𝑏𝑖𝑗 ,
untuk setiap elemen seletak.

› Perkalian dua matriks
𝐴 𝑚 x 𝑝= 𝑎𝑖𝑗 dan 𝐵𝑝 x 𝑛 = 𝑏𝑖𝑗 ,
diperoleh 𝐶 𝑚 x 𝑛 = 𝑐𝑖𝑗
Dengan mengalikan baris
matriks A terhadap kolom
matriks B.
Sifat-sifat yang berlaku
i. A x B  B x A
ii. A x I = I x A = A
iii. A x O = O x A = O
I = matriks identitas
O = matriks nol
› Perkalian skalar dengan matriks
A = 𝑎𝑖𝑗 dan k skalar
merupakan bilangan real, maka
kA = 𝑘𝑎𝑖𝑗 untuk setiap i dan
j.
Perkalian
HOME

› Sifat-sifat yang berlaku
i. (A + B)2 = A2 + B2 + AB + BA
ii. (A - B)2 = A2 + B2 – (AB + BA)
iii. (A + B)(A – B) = A2 – AB + BA - B2
› Ak = A x A x A x ... x A
(sebanyak k faktor)
dengan k bilangan bulat
positif dan A merupakan
matriks persegi berordo
m x m.
Perpangkatan
HOME
Contoh

1.2.1 Determinan Matriks Persegi Berordo 2 x 2
Matriks A berordo 2 x 2  A =
𝑎 𝑏
𝑐 𝑑
dinotasikan
dengan: det (A) = det
𝑎 𝑏
𝑐 𝑑
= 𝐴 = 𝑎𝑑 − 𝑏𝑐.
Determinan Matriks Persegi
HOME

› Cara Cramer
› Diberikan SPLDV
𝑎𝑥 + 𝑏𝑦 = 𝑚
𝑐𝑥 + 𝑑𝑦 = 𝑛
.
› Maka bentuk matriks:
›
𝑎 𝑏
𝑐 𝑑
𝑥
𝑦 =
𝑚
𝑛
1.2.2 Penyelesaian Sistem Persamaan Linear Dua
Variabel (SPLDV) dengan Determinan.
HOME

› Nilai x dan y ditentukan oleh:
› 𝑥 =
𝑚 𝑏
𝑛 𝑑
𝑎 𝑏
𝑐 𝑑
dan y =
𝑎 𝑚
𝑏 𝑛
𝑎 𝑏
𝑐 𝑑
, dengan
𝑎 𝑏
𝑐 𝑑
≠ 0
› Dx =
𝑚 𝑏
𝑛 𝑑
, Dy =
𝑎 𝑚
𝑐 𝑛
, dan D =
𝑎 𝑏
𝑐 𝑑
Contoh
HOME

i. Pindahkan dua kolom pertama dari
determinan kesebelah kanan
ii. Lakukan perkalian keenam diagonal.
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
𝑎 𝑏
𝑑 𝑒
𝑔 ℎ
= aei + bfg + cdh – gec –hfa - idb
› Perhatikan matriks
A =
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
› Determinan
matriks A dengan
cara Sarrus
dilakukan dengan
aturan berikut:
1.2.3 Determinan Matriks Persegi Berordo 3 x 3
-Cara Sarrus
HOME
(-) (-) (-)
(+) (+) (+)

›
𝑎 𝑐
𝑔 𝑖 = 𝑎𝑖 − 𝑔𝑐1. Pengertian Minor
Minor dari elemen umum
adalah determinan yang
berisi elemen setelah baris
dan kolom yang dihilangkan.
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
Cara Ekspansi Kofaktor
HOME
Penghilangan kolom ke-2
Penghilangan
baris ke-2

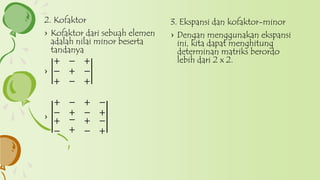
3. Ekspansi dan kofaktor-minor
› Dengan menggunakan ekspansi
ini, kita dapat menghitung
determinan matriks berordo
lebih dari 2 x 2.
2. Kofaktor
› Kofaktor dari sebuah elemen
adalah nilai minor beserta
tandanya
›
+ − +
− + −
+ − +
›
+ − + −
− + − +
+
−
−
+
+ −
− +

› Sifat 2
Jika ada semua elemen pada baris atau
pada kolom dari sebuah determinan
sama dengan nol.
0 0 0
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
= 0 atau
𝑎 𝑑 0
𝑏 𝑒 0
𝑐 𝑓 0
= 0
1.2.4 Sifat-sifat determinan
matriks persegi
› Sifat 1
𝐴 = 𝐴 𝑇
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
=
𝑎 𝑑 𝑔
𝑏 𝑒 ℎ
𝑐 𝑓 𝑖
› Sifat 3
Jika dua baris (atau dua kolom) dari
sebuah determinan saling ditukar, maka
tanda dari determinan akan berubah.
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
= (−)
𝑔 ℎ 𝑖
𝑑 𝑒 𝑓
𝑎 𝑏 𝑐
atau
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
= (−)
𝑎 𝑐 𝑏
𝑑 𝑒 𝑓
𝑔 𝑖 ℎ

› Sifat 4
Jika dua baris (atau dua kolom) dari sebuah determinan sama
atau kelipatannya, maka nilai determinan itu samadengan nol.
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑎 𝑏 𝑐
= 0 atau
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑘𝑎 𝑘𝑏 𝑘𝑐
= 0
› Sifat 5
Jika ada setiap elemen pada baris (atau kolom) dari sebuah
determinan dikali oleh bilangan real k, maka nilai determinan itu
bernilai k kali determinan matriks awal.
2 3𝑘 1
4 𝑘 3
3 5𝑘 7
= 𝑘
2 3 1
4 1 3
1 5 7

› Sifat 6
Jika masing-masing elemen pada baris (atau kolom)
dinyatakan sebagai jumlah dua suku (baris atau kolom),
maka determinan matriks tersebut merupakan jumlah
kedua determinan itu.
𝑎 + 𝑎 𝑏 𝑐
𝑑 + 𝑏 𝑒 𝑓
𝑔 + 𝑐 ℎ 𝑖
= 𝑘
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
+
𝑎 𝑏 𝑐
𝑏 𝑒 𝑓
𝑐 ℎ 𝑖

› Sifat 7
Nilai sebuah determinan tidak berudah, jika masing-masing
elemen pada baris (atau kolom) dikali dengan bilangan real k
dan ditambahkan pada sembarang baris (atau kolom).
𝑎 𝑏 𝑐 + 𝑘𝑎
𝑑 𝑒 𝑓 + 𝑘𝑑
𝑔 ℎ 𝑖 + 𝑘𝑔
=
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖

› Ketentuan determinan
matriks.
𝐷 𝑥 =
𝑏1 𝑎12 𝑎13
𝑏2 𝑎22 𝑎23
𝑏3 𝑎32 𝑎33
,
𝐷 𝑦 =
𝑎11 𝑏1 𝑎13
𝑎21 𝑏2 𝑎23
𝑎31 𝑏3 𝑎33
› Perhatikan SPLTV berikut.
𝑎11 𝑥 + 𝑎12 𝑦 + 𝑎13 𝑧 = 𝑏1
𝑎21 𝑥 + 𝑎22 𝑦 + 𝑎23 𝑧 = 𝑏2
𝑎31 𝑥 + 𝑎32 𝑦 + 𝑎33 𝑧 = 𝑏3
Model matematika SPLTV
berbentuk.
𝑎11 𝑎12 𝑎13
𝑎21 𝑎22 𝑎23
𝑎31 𝑎32 𝑎33
𝑥
𝑦
𝑧
=
𝑏1
𝑏2
𝑏3
1.2.5 Penyelesaian Sistem Persamaan Linear Tiga
Variabel (SPLTV) dengan Determinan.

› Penyelesaiannya adalah (x, y, z)
dan HP = (𝑥, 𝑦, 𝑧)› 𝐷𝑧 =
𝑎11 𝑎12 𝑏1
𝑎21 𝑎22 𝑏2
𝑎31 𝑎32 𝑏3
, 𝑑𝑎𝑛
› 𝐷 =
𝑎11 𝑎12 𝑎13
𝑎21 𝑎22 𝑎23
𝑎31 𝑎32 𝑎33
› Nilai x, y, dan z
› 𝑥 =
𝐷 𝑥
𝐷
, y =
𝐷 𝑦
𝐷
, z =
𝐷 𝑧
𝐷

1.3 Invers Matriks Persegi
Misalkan M merupakan matriks persegi berordo n x n
dan I matriks satuan (identitas) berordo n x n. Jika ada
sebuah matriks M-1 (dibaca: invers M) akan selalu
berlaku.
M-1  M = M  M-1 = I
Invers Matriks
HOME

A. Formula Matriks Persegi Berordo 2 x 2
Diberikan matriks A berordo
2 x 2:
𝐴 =
𝑎 𝑏
𝑐 𝑑
Invers matriks A ditentukan oleh:
𝐴−1
=
1
𝐷
𝑑 −𝑏
−𝑐 𝑎
dengan D = ad-bc
(i) Untuk D  0, matriks A disebut nonsingular berarti
mempunyai invers.
(ii) Untuk D = 0, matriks A disebut singular berarti tidak
mempunyai invers.
1.3.1 Invers Matriks Persegi Berordo 2 x 2
HOME

› Carilah A-1 dari A =
4 −1
−6 2
.
B. Menentukan Invers Matriks Berordo 2 x 2
dengan Eliminasi Gauss-Jordan

1.3.2 Invers Matriks Persegi
Berordo 3 x 3
Untuk menentukan invers
matriks persegi berordo 3 x 3
akan lebih mudah jika kita
menggunakan eliminasi
Gauss-Jordan.
Ordo 3 x 3
HOME

2 3
3 6
8
15
 𝐼 𝑋
Proses pencarian matriks
sebaga berikut.
1.3.5 Penyelesaian Sistem
Persamaan Linear (SPL)
dengan Eliminasi Gauss-
Jordan
2 3
3 6
𝑥
𝑦 =
8
15
.
Bentuk di atas dapat ditulis
dalam bentuk matriks Gauss-
Jordan sebagai berikut.
Eliminasi Gauss-Jordan
HOME

1.3.3 Persamaan Matriks
HOME
Persamaan matriks sama seperti persamaan bentuk aljabar.
Bentuk umum persamaan matriks adalah sebagai berikut.
(i) A  X = B  A-1A  X = A-1  B
I  X = A-1  B
X = A-1  B
(ii) X  A = B  X  A  A-1 = B  A-1
X  I = B  A-1
X = B  A-1

HOME
Dengan A =
2 3
3 6
, 𝑋 =
𝑥
𝑦 ,
𝑑𝑎𝑛 𝐵 =
8
15
.
Untuk menetukan
penyelesaian SPL berikut.
2𝑥 + 3𝑦 = 8
3𝑥 + 6𝑦 = 15
Dapat dilakukan dengan
menulis SPL dalam bentuk
matriks:
2 3
3 6
𝑥
𝑦 =
8
15
1.3.4 Penyelesaian Sistem Persamaan Linear (SPL)
Menggunakan Invers Matriks

Perhatikan SPL berikut
2 3
3 6
𝑥
𝑦 =
8
15
A B
›
2 3
3 6
8
15
 𝐼 𝑋
› Proses pencarian matriks X
sebagai berikut
1.3.5 Penyelesaian Sistem Persamaan Linear (SPL)
dengan Eliminasi Gauss-Jordan

Persiapkan diri Anda, pertemuan selanjutnya Ulangan Harian

�ݺ�ߣ

Matriks kelas xii K-13

Recommended

More Related Content

What's hot (20)

Similar to Matriks kelas xii K-13 (20)

Recently uploaded (20)

Matriks kelas xii K-13