Persamaan Eksponen
Download as docx, pdf5 likes29,019 views
Dokumen ini membahas tentang persamaan eksponen dalam matematika, termasuk berbagai bentuk dan metode penyelesaian. Terdapat penjelasan mengenai penggunaan logaritma dan sifat-sifat fungsi eksponen. Dokumen juga memberikan contoh-contoh soal dan proses penyelesaiannya.
![Persamaan Eksponen
Matematika Kelas 2 > Eksponen
395
< Sebelum
Sesudah >
Adalah persamaan yang didalamnya terdapat pangkat yang berbentuk
fungsi dalam x (x sebagai peubah).
[Ket. : Usahakan setiap bilangan pokok ditulis sebagai bilangan berpangkat
dengan bilangan dasar 2, 3, 5, 7, dst].
BENTUK-BENTUK
A. af(x) = ag(x) f(x) = g(x)
Samakan bilangan pokoknya sehingga pangkatnya
dapat
disamakan.
contoh :
2 SUKU SUKU DI RUAS KANAN, 1 SUKU DI RUAS KIRI
1. 82x-3) = (32x+1)1/4
(23)(2x-3)1/2 = (25)(x+1)1/4
2(6x-9)/2 = 2(5x-5)/4
(6x-9)/2 = (5x-5)/4
24x-36 = 10x+10
14x = 46
x = 46/14 = 23/7
2. 3x族-3x+2 + 3x族-3x = 10
3族.3x族-3x+3x族-3x = 10
9. 3x族-3x + 3x族-3x = 10
10. 3x族-3x = 10
3x族 - 3x = 30
x族 - 3x = 0
x(x-3) = 0
x1 = 0 ; x2 = 3
3 SUKU GUNAKAN PEMISALAN](https://image.slidesharecdn.com/persamaaneksponen-131202122217-phpapp01/85/Persamaan-Eksponen-1-320.jpg)
Persamaan Eksponen
- 1. Persamaan Eksponen Matematika Kelas 2 > Eksponen 395 < Sebelum Sesudah > Adalah persamaan yang didalamnya terdapat pangkat yang berbentuk fungsi dalam x (x sebagai peubah). [Ket. : Usahakan setiap bilangan pokok ditulis sebagai bilangan berpangkat dengan bilangan dasar 2, 3, 5, 7, dst]. BENTUK-BENTUK A. af(x) = ag(x) f(x) = g(x) Samakan bilangan pokoknya sehingga pangkatnya dapat disamakan. contoh : 2 SUKU SUKU DI RUAS KANAN, 1 SUKU DI RUAS KIRI 1. 82x-3) = (32x+1)1/4 (23)(2x-3)1/2 = (25)(x+1)1/4 2(6x-9)/2 = 2(5x-5)/4 (6x-9)/2 = (5x-5)/4 24x-36 = 10x+10 14x = 46 x = 46/14 = 23/7 2. 3x族-3x+2 + 3x族-3x = 10 3族.3x族-3x+3x族-3x = 10 9. 3x族-3x + 3x族-3x = 10 10. 3x族-3x = 10 3x族 - 3x = 30 x族 - 3x = 0 x(x-3) = 0 x1 = 0 ; x2 = 3 3 SUKU GUNAKAN PEMISALAN
- 2. 1. 22x + 2 - 2 x+2 + 1 = 0 22.22x - 22.2x + 1 = 0 Misalkan : 2x = p 22x = (2x)族 = p族 4p族 -4p + 1 = 0 (2p-1)族 = 0 2p - 1 = 0 p =1/2 2x = 2-1 x = -1 2. 3x + 33-x - 28 = 10 3x + 33/3x - 28 = 10 misal : 3x = p p + 27/p - 28 = 0 p族 - 28p + 27 = 0 (p-1)(p-27) = 0 p1 = 1 3x = 30 x1 = 0 p2 = 27 3x = 33 x2 = 3 B. af(x) = bf(x) f(x) = 0 Bilangan pokok berbeda, pangkat sama. Pangkatnya = 0. Contoh: 1. 3x族-x-2 = 7x族-x-2 x族 - x -2 = 0 (x-2)(x+1) = 0 x1 = 2 ; x2 = -1 C. af(x) = bf(x) f(x) log a = g(x) log b Bilangan pokok berbeda, pangkat berbeda. Diselesaikan dengan menggunakan logaritma. Contoh: 1. 4x-1 = 3x+1 (x-1)log4 = (x+1)log3 xlog4 - log4 = x log 3 + log 3 x log 4 - x log 3 = log 3 + log 4
- 3. x x x x (log4 - log3) = log 12 log 4/3 = log 12 log 4/3 = log 12 = log 12/ log 4/3 = 4/3 log 12 D. f(x) g(x) = f(x) h(x) Bilangan pokok (dalam fungsi) sama, pangkat berbeda.Tinjau beberapa kemungkinan. 1. Pangkat sama g(x) = h(x) 2. Bilangan pokok f(x) = 1 ket: 1g(x) = 1h(x) = 1 3. Bilangan pokok f(x) = -1 Dengan syarat, setelah nilai x didapat dari f(x)=-1 , maka nilai pangkatnya yaitu g(x) dan h(x) kedua-duanya harus genap atau kedua-duanya harus ganjil. ket : g(x) dan h(x) Genap : (-1)g(x) = (-1)h(x) = 1 g(x) dan h(x) Ganjil : (-1)g(x) = (-1)h(x) = -1 4. Bilangan pokok f(x) = 0 Dengan syarat, setelah nilai x didapat dari f(x) = 0, maka nilai pangkatnya yaitu g(x) dan h(x) kedua-duanya harus positif. ket : g(x) dan h(x) positif 0g(x) = 0h(x) = 0 Contoh: (x族 + 5x + 5)3x-2 = (x族 + 5x + 5)2x+3 1. Pangkat sama 3x - 2 = 2x + 3 x1 = 5 2. Bilangan pokok = 1 x族 + 5x + 5 = 1 x族 + 5x + 4 = 0 (x-1)(x-4) = 0 x2 = 1 ; x3 = 4 3. Bilangan pokok = -1 x族 - 5x + 5 = -1 x族 - 5x + 6 = 0 (x-2)(x-3) = 0 x = 1 ; x = 4
- 4. g(2) = 4 ; h(2) = 7 ; x=2 tak memenuhi karena (-1)4 (-1)7 g(3) = 7 ; h(3) = 9 ; x4 = 3 memenuhi karena (-1)7 = (-1)9 = -1 4. Bilangan pokok = 0 x族 - 5x + 5 = 0 x5,6 = (5 賊 5)/2 kedua-duanya memenuhi syarat, karena : g(2 1/2 賊 1/2 5) > 0 h(2 1/2 賊 1/2 5) > 0 Harga x yang memenuhi persamaan diatas adalah : HP : { x | x = 5,1,4,3,2 1/2 賊 1/2 5} Bilangan Pokok a > 0 1 Tanda Pertidaksamaan tetap/berubah tergantung nilai bilangan pokoknya a>1 af(x) > ag(x) f(x) > g(x) af(x) < ag(x) f(x) < g(x) (tanda tetap) 0<a<1 af(x) > ag(x) f(x) < g(x) af(x) < ag(x) f(x) > g(x) (tanda berubah) Catatan: Untuk memudahkan mengingat, bilangan pokok 0 < a < 1 diubah saja menjadi a = 1. Misal : 1/8 = (1/2)3 = 2-3 Contoh: 1. (1/2)2x-5 < (1/4)(1/2x+1) (1/2)2x-5 < (1/2)2(1/2x+1) Tanda berubah (0 < a < 1) 2x - 5 > x +2 x>7 2. 32x - 4.3x+1 + 27 > 0 (3x)族 - 4.31.3x + 27 > 0 misal : 3x = p p族 -12p + 27 > 0 (p - 9)(p - 3) > 0
- 5. p < 1 atau p > 9 3x < 31 3x > 3族 x < 1 atau x > 2
- 6. EKSPONEN 1. Pengertian Eksponen Bentuk an (baca : a pangkat n) disebut bentuk eksponensial atau perpangkatan dengan a disebut basis atau bilangan pokok dan n disebut eksponen atau pangkat. Jika n adalah bilangan bulat positif, maka : Berdasarkan penjelasan di atas maka berlaku rumus-rumus di bawah ini : Misalkan dan m,n adalah bilangan positif, maka: Contoh: Ubahlah bentuk ini Jawab: dalam bentuk pangkat positif :
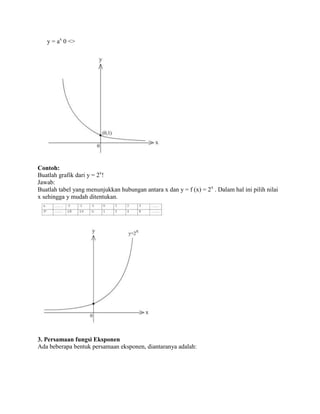
- 7. 2. Fungsi Eksponen dan Grafiknya Fungsi eksponen merupakan pemetaan bilangan real x ke ax dengan a > 0 dan dan , maka disebut fungsi eksponen mempunyai sifat-sifat : Kurva terletak di atas sumbu x (definit positif) Mempunyai asimtot datar y = 0 (sumbu x ) Monoton naik untuk a > 1 Monoton turun untuk 0 <> Grafik fungsi eksponen y = ax y = ax : a > 1 Jika a > 0
- 8. y = ax 0 <> Contoh: Buatlah grafik dari y = 2x! Jawab: Buatlah tabel yang menunjukkan hubungan antara x dan y = f (x) = 2x . Dalam hal ini pilih nilai x sehingga y mudah ditentukan. 3. Persamaan fungsi Eksponen Ada beberapa bentuk persamaan eksponen, diantaranya adalah:
- 9. F(x)=1 - Untuk f(x) 0 dan f(x) 1, maka f(x) = g(x) - f ( x ) = -1 asalkan f (x) dan g (x) sama-sama genap atau sama-sama ganjil, - f ( x ) = 0 asalkan f ( x ) > 0 dan g ( Contoh : Tentukan nilai x supaya Jawab: 4. Pertidaksamaan Eksponen f ( x ) > g ( x ), 0 > 1 f ( x ) <> Contoh: Himpunan bilangan real yang memenuhi pertidaksamaan Jawab: adalah.... x ) > 0
- 10. Jadi HP = { x | x > 2 }