Povijest matematike (History of Math)
1 like2,280 views
Dokument opisuje povijest matematike s fokusom na razvoj matematike misli od antike Grke do modernog doba, ukljuujui utjecajna djela i matematiare iz razliitih civilizacija kao 邸to su Sumerani, Egipani, i Kinezi. Istra転eni su va転ni matematiki koncepti i doprinosi, ukljuujui Pitagorin teorem i aritmetike metode kroz povijest. Projekt takoer ukljuuje aktivne aktivnosti uenika, kao 邸to su izlo転be i zajednika istra転ivanja s Grkom.
Povijest matematike (History of Math)
- 1. POVIJEST MATEMATIKE HISTORY OF MATH Gordana Divi, prof. mentor Srednja 邸kola Novska
- 2. History of Math eTwinning projekt Suraivali smo s Grkom Istra転ili smo: razvoj matematike misli od Sumerana do modernog doba istaknute matematiare od Antike Grke do modernog doba
- 3. to smo napravili? Prezentacije (.ppt) kojima smo predstavili: Sebe kolu Grad
- 4. to smo napravili? Izabrali LOGO projekta 13
- 5. to smo napravili? Posjetili smo izlo転bu Volim matematiku
- 6. to smo napravili? Organizirali smo Veer matematike
- 7. to smo napravili? Razmijenili estitke za Bo転i Na邸e estitke u Grkoj Grke estitke kod nas
- 8. to smo napravili? Obilje転ili Dan broja
- 9. to smo napravili? Kolege iz Grke posjetili su Tehniki muzej Antike Grke u Solunu
- 10. to smo napravili? Mjerili opseg Zemlje Eratostenov pokus Izraunali opseg Zemlje (39 635 km) Mjerili duljinu sjene 邸kole Raunali visinu 邸kole
- 11. ... and our outcome for Novska school is 8.322 m !!! Greek Team
- 12. and our outcome for Edessa school is , 賊 , Croatian Team
- 13. to smo napravili? Napisali dokumente (.doc i .ppt) o zadanim temama
- 14. to smo napravili? Predstavili projekt na 貼upanijskom vijeu nastavnika matematike Sisako-moslavake 転upanije (22. travnja 2015.)
- 15. to smo napravili? Postavili smo izlo転bu plakata u hodniku 邸kole
- 16. Pisali smo na forumu TwinSpacea rjenik matematikih pojmova s grkim korijenom na: Engleskom Grkom Hrvatskom to smo napravili?
- 17. to smo napravili? Napisali smo radove na zadane teme i spojili ih u jednu knjigu http://www.slideshare.net/gordanadivic/povijest- matematike-history-of-math Uredili smo TwinSpace projekta: http://twinspace.etwinning.net/490/home
- 19. Na邸e prvo znanje o matematici dolazi od Egipana i Babilonaca Babilonska matematika je datirana za 4000 godina prije Krista zajedno sa Sumeranima u Mezopotamiji
- 20. Malo se zna o Sumeranima Prvi put je naseljen 4500 i 4000 godina prije Krista Danas se ti ljudi zovu Ubaidiansi Jo邸 manje se zna o njihovoj matematici
- 21. Koristili su klinasto pismo, a pisali su na glinenim ploicama Koristili su preko 2000 znakova Slika 1. Sumerski zapis klinastim pismom
- 22. Razvili su heksagezimalni brojevni sustav koji su preuzeli Babilonci Babilonci, Asirci i Hiti su naslijedili sumerski zakon i knji転evnost i va転nije njihov nain pisanja Ono 邸to smo od Sumerana zadr転ali do danas je podjela tjedna na 7 dana, dana na 24 sata, sata na 60 minuta i minutu na 60 sekundi
- 23. Propa邸u Sumerske civilizacije u Mezopotamiji razvija se Babilonska Od Sumerana su naslijedili klinasto pismo i heksagezimalni brojevni sustav Slika 2. Znamenke u Babilonskom brojevnom sustavu
- 24. Za prikaz brojeva koristili su 2 osnovna oblika: Nisu imali sumbol za nulu ili decimalnu toku pa je bilo te邸ko tumaiti nalaz iz tog doba Slika 3. Babilonski simbol za broj 10 Slika 4. Babilonski prikaz za broj 1 ili 60
- 25. 40-ih godina pro邸log stoljea Njemaki povijesniari Otto Neugebauer i Abraham Sachs Primijetili kako reci na ploici zadovoljavaju zanimljivo svojstvo Ureene trojke prirodnih brojeva (a, b, c) koje zadovoljavaju jednakost a族+b族=c族
- 26. Dokaz postojanja Pitagorine trojke tisuama godine prije pojave matematiara antike Grke Slika 5. Plimpton 322
- 27. Nalazi邸te u Nipuru-naeno oko 50 000 glinenih ploica Svjedoe znatnom poznavanju matematike Slika 7. Nalazi邸te u Nipuru
- 28. Izgraivali su nizove koji ukljuuju trokutaste brojeve (1, 3, 6, 10 ,15...), kvadratne brojeve (1, 4, 9, 16, 25...) i piramidalne brojeve (1, 5, 14, 30, 50...) Slike 8. i 9. Prikazuju nizove brojeva
- 29. Primjer kori邸tenja niza piramidalnih brojeva je slaganje municije u Calcutti i lako izraunavanje broja uladi Slika 10. Slo転ena municija u Calcutti
- 31. Moskovski papirus - otkriven je 1893., a autor je nepoznat - najvea dostignua egipatske geometrije - du転ine je oko pola metra i 邸irine manje od 8 cm - uva se u Moskovskom muzeju
- 33. Rhindov papirus 1858. otkrio ga je 邸kotski egiptolog Henry Rhind u Luxoru Napisao ga je pisar Ahmes oko 1600. pr. Kr. Dug je 6 metara , 邸irok 30 cm, uva se u British Museumu u Londonu
- 34. Zbirka tablica i vje転bi sa 87 matematikih problema U njemu se nalaze i najstariji poznati i sauvani zapis broja Rhindov papirus
- 35. Brojevi Egipani su koristili brojevni sustav s bazom 10 broj 1339
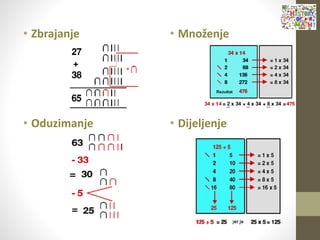
- 36. Zbrajanje Oduzimanje Mno転enje Dijeljenje
- 37. Razlomci Poznavali su samo jedinine razlomke Iznimka je bio 2/3 Razlomke su tvorili tako 邸to su kombinirali pojedine dijelove simbola oka boga Horusa. cjelokupni simbol oka ima vrijednost 1
- 38. Geometrija Za izgradnju piramida i hramova Egipani su morali imati dobro razvijenu geometriju i stereometriju Znali su raunati nagib i obujam piramide, te obujam krnje piramide
- 39. Algebra Staroegipatska algebra bila je retorika problemi i rje邸enja dani su rijeima Koristili su se sedmeroznamenkastim brojevima, a u svojim raunima imali su mje邸avinu jednostavnosti i kompliciranosti
- 41. temeljena na grkim tekstovima razvijena od 7. st. pr. Kr. do 4. st. po. Kr. du転 istonih obala Mediterana matematika grki mathema znanost kori邸tenje opih matematikih dokaza i teorija
- 43. presjedali najva転nijom i najdramatinijom revolucijom u matematici ikad osnovni cilj: shvaanje ovjekova mjesta u svemiru matematika dosegla najvi邸i nivo razvitka poeli upotrebljavati papirus grki doprinos matematike u tri faze: 1. od Talesa i Pitagore do Demokrita 2. Euklidov sustav 3. Aleksandrijska faza
- 44. Tales osniva grke matematike nema dokumentiranih dokaza klasina filozofija pomogla da se rekonstruiraju tekstovi iz bli転eg perioda izdanja Euklida, Arhimeda, Apolonija itd. te邸ko pratiti tijek povijesnog razvitka o grkoj matematici zakljuujemo pomou: manjih sastavnica i zapa転anja filozofa i drugih autora
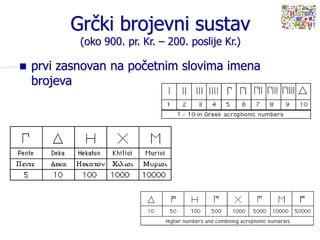
- 45. Grki brojevni sustav (oko 900. pr. Kr. 200. poslije Kr.) prvi zasnovan na poetnim slovima imena brojeva
- 46. drugi je upotrebljavao sva slova iz grkog alfabeta i tri iz fenikog baza 10
- 47. ideja dokaza i deduktivna metoda kori邸tenja logikih koraka za dokazivanje ili opovrgavanje teorija dalo je matematici snagu osigurava da su dokazane teorije istinite postavilo temelje za sustavni pristup matematici Najva転niji doprinos Grka
- 49. Openito... prvi pravi matematiar roen na grkom otoku Samosu Tales ga je zainteresirao za matematiku otputovao je u Egipat oko 535. pr. Kr. osnovao je Pitagorejsku skolu danas ga svi znamo po Pitagorinom pouku
- 50. Kroz 転ivot... filozof u Egiptu hramski sveenik u Diospolisu zarobljenik u Babilonu o転enio se u 60. godini gladovao do smrti najsavr邸eniji broj 10 broj bit u filozofiji
- 51. Pitagorejska 邸kola osnovana u Krotoni naglasak na tajnosti i zajedni邸tvu Pitagorin pouak otkrie iracionalnih brojeva pet pravilnih geometrijaskih tijela
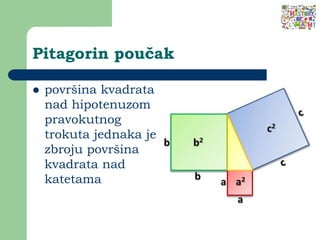
- 52. Pitagorin pouak povr邸ina kvadrata nad hipotenuzom pravokutnog trokuta jednaka je zbroju povr邸ina kvadrata nad katetama
- 53. Pitagorine trojke 3, 4, 5 9+16=25 Egipatski trokut mo転emo dobiti jo邸 beskonano mnogo Pitagorinih trojki tako 邸to emo brojeve 3, 4 i 5 umno転avati istim brojem 6, 8 i 10 36+64=100
- 54. PLATON (428.-347.god. p.n.e.) -転ivio i djelovao u Ateni -387.g.p.n.e. osnovao filozofsku 邸kolu AKADEMIJU u kojoj se pouavala i matematika aritmetika, trigonometrija i planimetrija Slika 1.Platon Marija Ko転ari, 4.g
- 55. Neka ne ulazi onaj koji ne zna geometriju! Slika 2. Natpis na ulazu u Akademiju
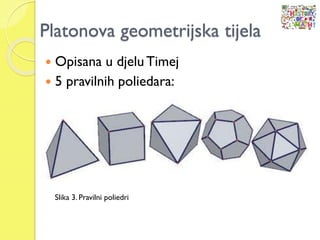
- 56. Platonova geometrijska tijela Opisana u djeluTimej 5 pravilnih poliedara: Slika 3. Pravilni poliedri
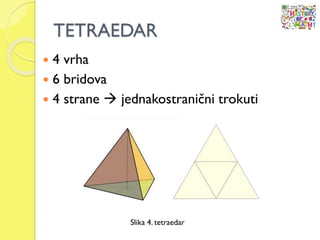
- 57. TETRAEDAR 4 vrha 6 bridova 4 strane jednakostranini trokuti Slika 4. tetraedar
- 58. HEKSAEDAR Kocka 8 vrhova 12 bridova 6 stranakvadrati Slika 5. heksaedar
- 59. OKTAEDAR 6 vrhova 12 bridova 8 strana jednakostranini trokuti Slika 6. oktaedar
- 60. DODEKAEDAR 20 vrhova 30 bridova 12 stranapravilni peterokut Slika 7. dodekaedar
- 61. IKOZAEDAR 12 vrhova 30 bridova 20 stranajednakostranini trokuti Slika 8. ikozaedar
- 63. u 2. tisuljeu pr.Kr. u Kini su imali simbole za brojeve raunali su 邸tapiima dok se u 16. st. nije pojavio abakus Slika 1. kineski brojevi Slika 2. abakus ne zna se mnogo o matematici drevne Kine, no prilino je sigurno da poeci astronomije i matematike drevne Kine se転u barem u 2. tisuljee pr.n.e. ,u to doba Kinezi su ve imali detaljno razraen kalendar najstariji sauvani matematiki tekstovi potjeu tek iz doba oko 200. pr.Kr.
- 64. Doprinosi kineskih matematiara: Sveta knjiga o aritmetici (2. 12.st.) indirektno govori o Pitagorinom pouku Aritmetika u devet knjiga (oko 150. g.pr.Kr.) - postupak izraunavanja povr邸ine trokuta, etverokuta, kruga, kru転nog odsjeka i isjeka, obujam prizme, piramide, valjka, sto邸ca, prikraene (krnje) piramide i sto邸ca Knjiga o mijenama (I Ching) - jedna od najstarijih ouvanih knjiga - koristila se za proricanje i gatanje, sadr転i elemente binarne notacije brojeva
- 65. Poznati matematiari: Zhang Qiu-Jian (5. st.) - dao je formulu za sumu aritmetikog niza Tsu Chung chih (430. 500.) za vrijednost broja uzima daje 邸est tonih decimalnih mjesta Quin Jiu - Shao (1202. -1261.) - tra転io je rje邸enja jednad転bi metodom koju nazivamo Hornerova (William Horner, 1819.), iako je u Kini bila poznata 500 godina ranije Chu Shih - kieh (1270. - 1330.) - napisao je dva va転na teksta koji su vrhunac kineske matematike, tekstovi sadr転e Pascalov trokut binomnih koeficijenata, koji je u Kini poznat etiri stoljea prije no 邸to ga je Pascal otkrio.
- 67. u staroindijskoj matematici nema velikih djela iskljuivo posveenih matematici; matematika je prisutna tek kao dio, kao pojedinano poglavlje u astronomskim ili astrolo邸kim djelima najstariji poznati matematiki tekstovi su Sulvasutre, dodaci vjerskim tekstovima u njima se nalaze pravila za mjerenje i izgradnju hramova i oltara na razini elementarne geometrije karakteristike indijskih matematikih tekstova je da su openito pisani u stihovima Slika 1. indijski brojevi
- 68. Staroindijskimatematiari: Aryabhatta (476. 550.) - znao je vaditi drugi i trei korijen podjelom radikanda u grupe dao je tone formule za povr邸inu trokuta i kruga, pi邸e o, kvadratnim jednad転bama, potencijama Brahmagupta (598. oko 670.) Brahmaguptina formula: poopenje Heronove formule na tetivne etverokute;
- 69. Mahavira (9. st.) bavio se elementarnom matematikom i prvi je indijski matematiar koji je napisao samo matematici posveen tekst Bhaskara (1114. 1185.) - najpoznatiji je indijski matematiar do 12. stoljea, puno je doprinjeo razumijevanju brojevnih sustava i rje邸avanju jednad転bi, dokazivao je i Pitagorin pouak glavna su mu matematika djela Lilavati i Bijaganita, bavio se ravninskom i sfernom trigonometrijom,
- 71. dana邸nja matematika zapadnog stila mnogo je slinija matematici kakvu susreemo u arapskim doprinosima, nego onoj u starogrkim, mnoge ideje koje su pripisane Europljanima pokazale su se zapravo arapskim Slika 1. arapski brojevi
- 72. Arapski matematiari: Al-Karaji (953.g. - 1029.g.) - smatra se prvom osobom koja je potpuno oslobodila algebru od geometrijskih operacija i zamijenila ih aritmetikim osnovao je utjecajnu algebarsku 邸kolu koja e uspje邸no raditi vi邸e stoljea
- 73. Al-Haytham (965.g. - 1040.g.) je vjerojatno prvi koji je poku邸ao klasificirati parne savr邸ene brojeve takoer je prva poznata osoba koja je izrekla Wilsonov teorem (ako je p prost broj, onda p dijeli 1 + (p - 1)!), nije jasno je li to znao dokazati Omar Khayyam (1048.g. 1131.g.) uz matematiku bavio se astronomijom, filozofijom i poezijom dao je potpunu klasifikaciju kubnih jednad転bi (14 tipova) i prvi uoio da ne moraju imati jedinstveno rje邸enje
- 74. (12. 13. stoljee) Slika 1. FibonacciBarbara Ma邸unjac, 4.g
- 75. talijanski matematiar mladost proveo u Arabiji temelj njegove matematike je broj iza sebe ostavio niz otkria
- 76. FIBONACCIJEV NIZ Slika 2. Fibonaccijev niz
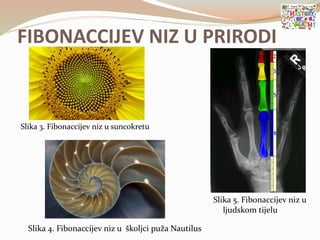
- 77. FIBONACCIJEV NIZ U PRIRODI Slika 3. Fibonaccijev niz u suncokretu Slika 4. Fibonaccijev niz u 邸koljci pu転a Nautilus Slika 5. Fibonaccijev niz u ljudskom tijelu
- 78. FIBONACCIJEV NIZ U UMJETNOSTI Slika 6. Fibonaccijev niz u portretu Mona Lise Slika 7. Fibonaccijev niz u Partenonu
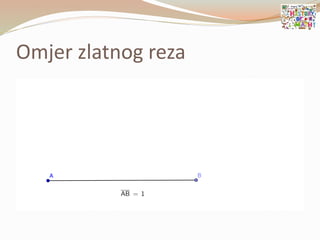
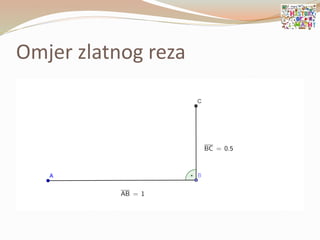
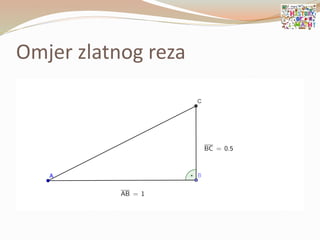
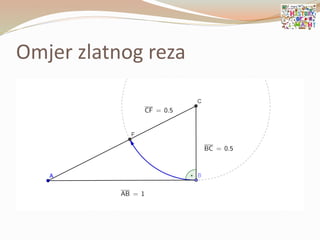
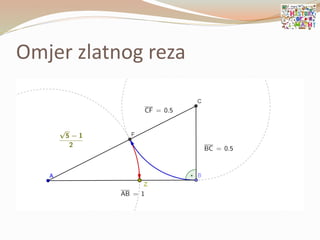
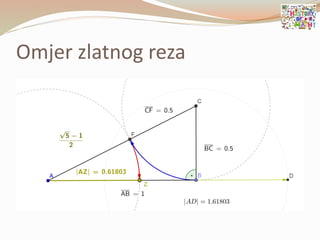
- 79. Bo転anski omjer ili omjer Zlatnog reza = 1 + 5 2 1.618033989
- 86. LIBER ABACI najpoznatije djelo o aritmetici jedna od prvih zapadnih knjiga u kojoj su opisane arapske brojke etiri dijela Slika 8. Liber Abaci
- 87. JOHN NAPIER Laura Ilii, 3.g
- 88. OPENITO: roen u Edinburghu 1550.god, a umro 4.travnja 1617.god Upisao se na sveuili邸te St. Andrews Diplomu je stekao u Parizu, te je nakon toga boravio u Nizozemskoj i Italiji Poznat je u matematikim i in転enjerskim krugovima Najpoznatiji je kao izumitelj logaritama, Napierovih kostiju, te popularizaciji decimalnog zareza Radio je na podrujima matematike, fizike, astronomije i astrologije
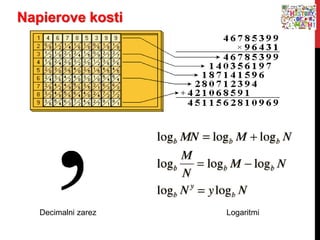
- 89. Napierove kosti Decimalni zarez Logaritmi
- 90. NAJPOZNATIJA DJELA Plaine Discovery of the Whole Revelation of St. John, 1593. Statistical Account Mirifici logarithmorum canonis descriptio, 1614. Construction of Logarithms, 1619.
- 91. Mirifici logarithmorum canonis descriptio, Statistical Account i Construction of Logarithms
- 92. Henry Briggs engleski matematiar Profesor geometrije u Oxfordu roen u Warleywoodu u Yorkshireu 1561. studirao je na St. Johns Collegeu u Cambridgeu Patricia Kujund転i, 3.g
- 93. kao profesor na Oxfordu saznaje za Napiera 1615. putuje k njemu u Edinburgh Napier se sla転e s Briggsovim prijedlogom za logaritme s bazom 10 Nakon Napierove smrti nastavja njegov rad 1624. objavljuje tablicu Arithmetica Logarithmica Umro je u Oxfordu 1630.
- 94. Blaise Pascal Antonio Horaek, 4.g
- 95. 貼ivotopis Blaise Pascal Blaise Pascal bio je francuski matematiar, fiziar, izumitelj, pisac i kr邸anski filozof. Bio je ''udo od djeteta'', a 邸kolovao ga je otac. Pascalovi najraniji poslovi bili su u primjenjenim i prirodnim znanostima, gdje je doprinio prouavanju tekuina te je pojasnio pojmove tlaka i vakuuma generalizacijom rada EvangelistaTorricellija.
- 96. Pascalov prvi stroj za raunanje
- 97. Pascalov doprinos matematici Prvi znaajan rad, Blaise je napisao sa samo 邸esnaest godina, a bio je to osnovni nacrt njegove uvene rasprave o presjecima sto転ca.
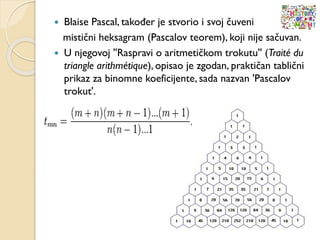
- 98. Blaise Pascal, takoer je stvorio i svoj uveni mistini heksagram (Pascalov teorem), koji nije sauvan. U njegovoj ''Raspravi o aritmetikom trokutu'' (Trait辿 du triangle arithm辿tique), opisao je zgodan, praktian tablini prikaz za binomne koeficijente, sada nazvan 'Pascalov trokut'.
- 99. Pascalov doprinos fizici Njegov rad na podruju hidordinamike i hidrostatike bio je usmjeren na naelima hidraulikih tekuina. Njegovi izumi ukljuuju hidrauliku pre邸u (koristi hidraulini tlak da umno転i snagu) i 邸pricu. Hidrostatski tlak poveava se dubinom, djeluje jednako u svim smjerovima te je jednak na svim mjestima na istoj dubini.
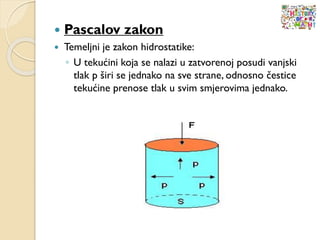
- 100. Pascalov zakon Temeljni je zakon hidrostatike: U tekuini koja se nalazi u zatvorenoj posudi vanjski tlak p 邸iri se jednako na sve strane, odnosno estice tekuine prenose tlak u svim smjerovima jednako.
- 102. Gottfried Wilhelm Leibniz Leipzig 1.7.1646. Filozof, matematiar, fiziar i diplomat Pretea Georgea Boolea i simbolike logike diferencijal i integral 1559. Francuska akademija znanosti Prvi model raunalnog stroja Slika 1.1.: Gottfried Wilhelm LeibnizSlika 1.2.: Leibnizovo mehaniko raunalo
- 103. Isaac Newton Woolsthorpe-by-Colsterworth 4.1.1643. Astronom, matematiar i fiziar Metode fluksije Opi zakon gravitacije Zrcalni teleskop Kraljevska akademija Slika 2.1.: Isaac Newton Slika 2.2.: Zrcalni teleskop
- 104. Infinitezimalni raun Fukcije, derivacije, integralne granine vrijednosti i limesi funkcije Diferencijalni raun Integralni raun Slika 3.1.: Integral Slika 3.2.: Derivacija
- 105. Newton Leibnizova formula Ako je po volji odabrana primitivna funkcija funkcije na intervalu , , onda vrijedi: = ()
- 106. Povijest infinitezimalnog rauna 5. st. pr. Kr.- Zenon 4. st. pr. Kr.- Eudokso 225. g. pr. Kr.- Arhimed 17. st.- Bonaventura Francesco Cavalieri Slika 4.1.: Metoda ekshaustije Slika 4.2.: Geometria indivisibilibus continuorum nova quadam ratione promota
- 107. Sukob Newtona i Leibniza Isaac Newton- 1671.- De Methodis Serierum et Fluxionum (objavljen 60 godina kasnije), fizikalni pristup Gottfried Wilhelm Leibniz- 1684.- prvi objavljeni rezultati, geometrijski pristup Slika 5.2.: De Methodis Serierum et Fluxionum Slika: 5.3.: Transactions of the Royal Society of London
- 108. ABRAHAM DE MOIVRE Iva Ciprijanovi, 4.g
- 109. DE MOIVREOVI POETCI: roen je u mjestu Vitry u Francuskoj, 26.svibnja 1667.godine. francuski matematiar poznat po formuli koja povezuje kompleksne brojeve i trigonometriju Bio je protestant, pa je neko vrijeme nakon edikta iz Nantesa (1685.) proveo u zatvoru, a nakon toga se odselio u Englesku gdje je pro転ivio ostatak svog 転ivota.
- 110. Za 転ivot je zaraivao kao privatni uitelj matematike te je uenike poduavao u njihovim domovima, ali i u londonskim kafiima. Nadao se da e jednom postati profesor matematike, ali u svakoj dr転avi je zbog neega bio diskriminiran.
- 111. DE MOIVREOVA ANEGDOTA: Njegova poznata anegdota je da je predvidio dan svoje smrti tako 邸to je utvrdio da svaki dan spava po 15 minuta dulje te je sumacijom odgovarajueg aritmetikog niza izraunao da e umrijeti na dan kad prespava puna 24 sata, i bio je u pravu.
- 112. THE DOCTRINE OF CHANCE: A METHOD OF CALCULATING THE PROBABILITIES OF EVENTS IN PLAY Glavno De Moivrevo djelo U toj se knjizi mo転e nai definicija statistike nezavisnosti dogaaja te niz zadataka vezanih za razne igre. Slika 1. De Moivrevo djelo :The Doctrine of Chance: A method of calculating the probabilities of events in play
- 113. DE MOIVREOVE FORMULE: Slika 2. Formula za binomne koeficijente Slika 3. Formula kojom je mogao dokazati sve cjelobrojne brojeve n Slika 4. Poznata DE MOIVREOVA formula
- 114. Slika 1. Johann Carl Friedrich Gauss Marta uri, 3.g
- 115. njemaki matematiar (1777. 1855.) osim matematikom, bavio se astronomijom, fizikom, geodezijom i topografijom osmislio neeuklidsku geometriju sa 邸esnaest godina s dvadeset i etiri godine objavio je majstorsko djelo Disquisitiones Arithmeticae 1801. je prema njegovim izraunima otkriven planetoid Ceres otkrio Kirchhoffove zakone napravio primitivni telegraf stvorio vlastite novine - Magnetischer Verein
- 116. Slika 2. Disquisitiones Arithmeticae Slika 3. Magnetischer Verein
- 117. osmislio br転i nain rje邸avanja zadataka zbrajanja brojeva od 1 do 100: (1 + 100) + (2 + 99) + ... + (50 + 51) = 50 * 101 = 5050 spoznao kriterij konstruiranja pravilnog sedamnaesterokuta dokazao osnovni teorem algebre stvorio Gaussovu ravninu stvorio Gaussovu krivulju koja se koristi u mnogim znanostima, posebno u psihologiji
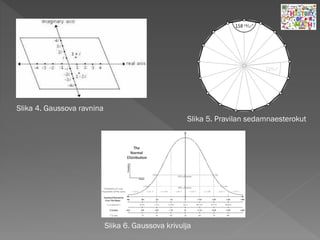
- 118. Slika 4. Gaussova ravnina Slika 5. Pravilan sedamnaesterokut Slika 6. Gaussova krivulja
- 119. John Nash Lana Matievi, 3.g
- 120. John Nash (1928.) je ekonomist i matematiar. Objavio je nekoliko teorija koje ste koriste i koje su doprinjele ekonomiji. Osvojio je 1994. godine Nobelovu nagradu za ekonomiju. Njegova najpoznatija teorija je: Nash Equilibrium (teorija igara)
- 121. to je Nashov Equilibrium? Koncept koji je na poetku bio napravljen kao taktika za jednostavne igre Nije najbolja strategija koja se mo転e iskoristiti, ali je najbolja taktika da se ne koriste drugi igrai kako bi se do邸lo do cilja
- 122. Zanimljivosti Patio od shizofrenije (do 1990.) Film Beautiful mind je snimljen o njegovom 転ivotu.
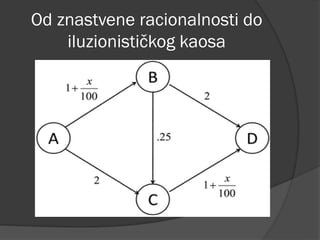
- 123. Od znastvene racionalnosti do iluzionistikog kaosa
- 124. Jednand転ba N.E.