PRML 第14章
- 1. 1/50 PRML 第 14 章 宮澤 彬 総合研究大学院大学 博士前期 miyazawa-a@nii.ac.jp September 25, 2015 (modi?ed: October 4, 2015)
- 2. 2/50 はじめに このスライドの LuaLATEX のソースコードは https://github.com/pecorarista/documents にあります. 教科書とは若干異なる表記をしている場合があります. 図は TikZ で描いたものを除き,Bishop (2006) のサポートペー ジ http://research.microsoft.com/en-us/um/people/ cmbishop/prml/ または Murphy (2012) のサポートページ http://www.cs.ubc.ca/~murphyk/MLbook/ から引用しています. 間違った記述を見つけた方は連絡ください.
- 3. 3/50 今日やること 1. ベイズモデル平均化 2. コミッティ 3. ブースティング (AdaBoost) 分類 回帰 4. 木構造モデル (CART) 回帰 分類 5. 条件付き混合モデル
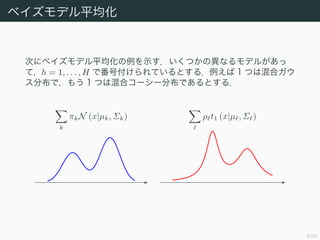
- 5. 5/50 モデルの結合 モデルの結合とベイズモデル平均化を混同しないように注意する. まずはモデル結合の例として,混合ガウス分布の密度推定を考える.モ デルは,データがどの混合要素から生成されたかを示す潜在変数 z を 使って,同時確率 p (x, z) で与えられる.観測変数 x の密度は p (x) = z p (x, z) (14.3) = K k=1 πkN (x|?k, Σk) (14.4) となる.データ X = (x1, . . . , xN ) に関する周辺分布は p (X) = N n=1 p (xn) = N n=1 zn p (xn, zn) (14.5) であり,各 xn に対して zn が存在していることがわかる.
- 6. 6/50 ベイズモデル平均化 次にベイズモデル平均化の例を示す.いくつかの異なるモデルがあっ て,h = 1, . . . , H で番号付けられているとする.例えば 1 つは混合ガウ ス分布で,もう 1 つは混合コーシー分布であるとする. k πkN (x|?k, Σk) ρ t1 (x|? , Σ )
- 7. 7/50 ベイズモデル平均化 モデルに関する事前確率が p (h) で与えられているならば,データに関 する周辺分布は次式で求められる. p (X) = H h=1 p (X|h) p (h) (14.6) モデル結合との違いは,データを生成しているのはモデル h = 1, . . . , H のどれか 1 つだということである.
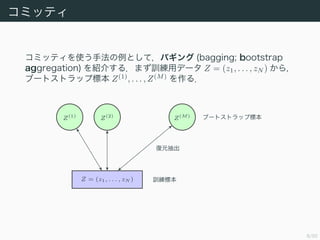
- 8. 8/50 コミッティ コミッティを使う手法の例として,バギング (bagging; bootstrap aggregation) を紹介する.まず訓練用データ Z = (z1, . . . , zN ) から, ブートストラップ標本 Z(1) , . . . , Z(M) を作る. Z(1) Z(2) Z(M) Z = (z1, . . . , zN ) 復元抽出 ブートストラップ標本 訓練標本
- 9. 9/50 コミッティ バギングにおけるコミッティの予測値 yCOM (x) は,各ブートストラッ プ集合 Z(1) , . . . , Z(M) で学習したモデルの予測 y1 (x) , . . . , yM (x) を 使って yCOM (x) = 1 M M m=1 ym (x) (14.7) となる. これで実際に良い結果が得られるのか,誤差を評価して確認する.
- 10. 10/50 バギングの誤差評価 予測したい回帰関数を h (x) とし,各モデルの予測値 ym (x) が,h (x) と加法的な誤差 εm (x) を使って ym (x) = h (x) + εm (x) (14.8) と表せると仮定する.このとき,二乗誤差は E (ym (x) ? h (x)) 2 = E (εm (x)) 2 (14.9) となるので,平均二乗誤差の期待値 EAV は EAV := E 1 M M m=1 (ym (x) ? h (x)) 2 = 1 M M m=1 E (εm (x)) 2 (14.10) で求められる.
- 11. 11/50 バギングの誤差評価 一方,コミッティによる出力について,誤差の期待値 ECOM は ECOM := E ? ? 1 M M m=1 ym ? h (x) 2 ? ? = E ? ? 1 M M m=1 εm (x) 2 ? ? (14.11) と求められる.ベクトル (1 · · · 1) ∈ RM と (ε1 (x) · · · εm (x)) ∈ RM に対して Cauchy-Schwarz の不等式を用いると M m=1 εm (x) 2 ≤ M M m=1 (εm (x)) 2 ECOM ≤ EAV が成り立つ.つまりコミッティを使う場合の誤差の期待値は,構成要素 の誤差の期待値の和を超えない.
- 12. 12/50 バギングの誤差評価 特に誤差の平均が 0 で無相関である,すなわち E [εm (x)] = 0 (14.12) cov (εm (x) , ε (x)) = E [εm (x) ε (x)] = 0, m = (14.13) が成り立つならば 1 ECOM = E ? ? 1 M M m=1 εm (x) 2 ? ? = 1 M2 E M m=1 (εm (x)) 2 = 1 M EAV (14.14) となり,誤差の期待値が大幅に低減される. 1 同じようなモデルを,同じような訓練データで学習させているのだから,こんなことは 期待できない.
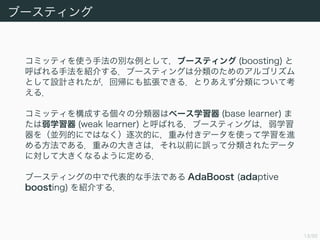
- 13. 13/50 ブースティング コミッティを使う手法の別な例として,ブースティング (boosting) と 呼ばれる手法を紹介する.ブースティングは分類のためのアルゴリズム として設計されたが,回帰にも拡張できる.とりあえず分類について考 える. コミッティを構成する個々の分類器はベース学習器 (base learner) ま たは弱学習器 (weak learner) と呼ばれる.ブースティングは,弱学習 器を(並列的にではなく)逐次的に,重み付きデータを使って学習を進 める方法である.重みの大きさは,それ以前に誤って分類されたデータ に対して大きくなるように定める. ブースティングの中で代表的な手法である AdaBoost (adaptive boosting) を紹介する.
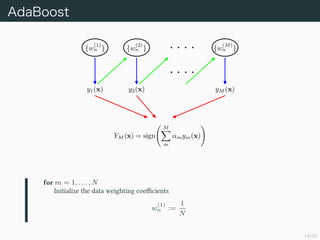
- 14. 14/50 AdaBoost {w (1) n } {w (2) n } {w (M) n } y1(x) y2(x) yM (x) YM (x) = sign M m αmym(x) for m = 1, . . . , N Initialize the data weighting coe?cients w (1) n := 1 N
- 15. 15/50 AdaBoost for m = 1, . . . , M Fit a classi?er ym (x) to the training data by minimizing Jm := N n=1 w (m) n 1{x | ym(x)=tn} (xn) . (14.15) Evaluate αm := log 1 ? εm εm (14.17) where εm := N n=1 w (m) n 1{x | ym(x)=tn} (xn) N n=1 w (m) n . (14.15) Update the data weighting coe?cients w (m+1) n := w (m) n exp αm1{x|ym(xn)=tn} (xn) . (14.18)
- 16. 16/50 AdaBoost Make predictions using the ?nal model, which is given by YM (x) := sign M m=1 αmym (x) . (14.19) このアルゴリズム中に現れる式は,指数誤差の逐次的な最小化から導か れる.
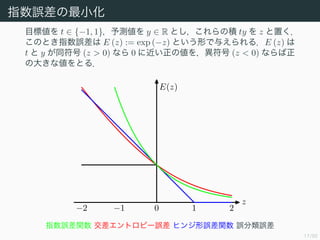
- 17. 17/50 指数誤差の最小化 目標値を t ∈ {?1, 1},予測値を y ∈ R とし,これらの積 ty を z と置く. このとき指数誤差は E (z) := exp (?z) という形で与えられる.E (z) は t と y が同符号 (z > 0) なら 0 に近い正の値を,異符号 (z < 0) ならば正 の大きな値をとる. ?2 ?1 0 1 2 z E(z) 指数誤差関数 交差エントロピー誤差 ヒンジ形誤差関数 誤分類誤差
- 18. 18/50 指数誤差の最小化 以下の誤差 E を最小化したい. E := N n=1 exp ?tn m =1 1 2 α y (xn) 逐次的に学習していくので α1, . . . , αm?1 と y1 (x) , . . . , ym?1 (x) は所与 として,αm と ym (x) に関して E を最小化する.E を E = N n=1 exp ?tn m?1 =1 1 2 α y (xn) ? 1 2 tnαmym (xn) = N n=1 w(m) n exp ? 1 2 tnαmym (xn) (14.22) と書き換える.ここで以下のように置いた. w(m) n := exp ?tn m?1 =1 1 2 α y (xn) (14.22 )
- 19. 19/50 指数誤差の最小化 ym : x → {?1, 1} によって正しく分類されたデータ点の添字集合を Tm, 誤って分類されたデータの添字集合を Mm とする.このとき E = e?αm/2 n∈Tm w(m) n + eαm/2 n∈Mm w(m) n = eαm/2 ? e?αm/2 N n=1 w(m) n 1{x|ym(xn)=tn} (xn) + e?αm/2 N n=1 w(m) n (14.23) が成り立つ.これを ym (x) について最小化することは (14.15) を最小化 することと同値である.
- 20. 20/50 指数誤差の最小化 また αm について微分して 0 と置くと eαm/2 + e?αm/2 N n=1 w(m) n 1{x|ym(xn)=tn} (xn) ? e?αm/2 N n=1 w(m) n = 0 eαm + 1 = N n=1 w(m) n N n=1 w(m) n 1{x|ym(xn)=tn} (xn) となる.(14.15) と同じ置き換えを行うことにより αm = log 1 ? εm εm を得る.これはアルゴリズム中の (14.17) に等しい.
- 21. 21/50 指数誤差の最小化 重みは (14.22 ) に従い次のように更新する. w(m+1) n = w(m) n exp ? 1 2 tnαmym (xn) (14.24) ここで tnym (xn) = 1 ? 21{x|ym(x)=tn} (xn) (14.25) が成り立つことを使うと w(m+1) n = w(x) n exp ? 1 2 αm 1 ? 21{x|ym(x)=tn} (xn) = w(x) n exp ? αm 2 exp 1{x|ym(x)=tn} (xn) (14.26) と書き換えられる.exp (?αm/2) はすべてのデータに共通なので無視す ると (14.18) が得られる.
- 22. 22/50 ブースティングのための誤差関数 以下の指数誤差を考える. E [exp (?ty (x))] = t∈{?1,1} exp (?ty (x)) p (t|x) p (x) dx (14.27) 変分法を使って y について上式を最小化する. ?t (y) := exp (?ty (x)) p (t|x) p (x) とする.停留点は以下のように求め られる. t∈{?1,1} Dy?t (y) = 0 exp (y (x)) p (t = ?1|x) ? exp (?y (x)) p (t = 1|x) = 0 y (x) = 1 2 log p (t = 1|x) p (t = ?1|x) (14.28) つまり AdaBoost は逐次的に p (t = 1|x) と (t = ?1|x) の比の対数の近 似を求めている.これが最終的に (14.19) で符号関数を使って分類器を 作った理由となっている.
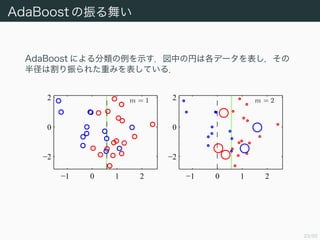
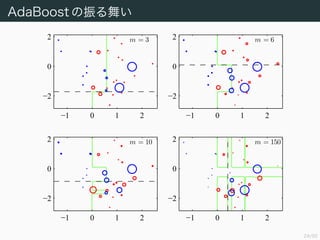
- 23. 23/50 AdaBoost の振る舞い AdaBoost による分類の例を示す.図中の円は各データを表し,その 半径は割り振られた重みを表している. m = 1 ?1 0 1 2 ?2 0 2 m = 2 ?1 0 1 2 ?2 0 2
- 24. 24/50 AdaBoost の振る舞い m = 3 ?1 0 1 2 ?2 0 2 m = 6 ?1 0 1 2 ?2 0 2 m = 10 ?1 0 1 2 ?2 0 2 m = 150 ?1 0 1 2 ?2 0 2
- 25. 25/50 AdaBoost の拡張 AdaBoost は Freund and Schapire (1996) で導入されたが,指数 誤差の逐次的最小化としての解釈は Friedman et al. (2000) で与えら れた.これ以降,誤差関数の変更により様々な拡張が行われるように なった.
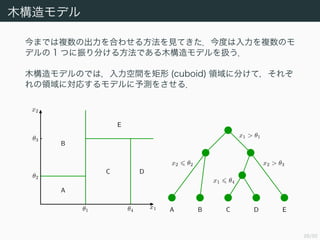
- 26. 26/50 木構造モデル 今までは複数の出力を合わせる方法を見てきた.今度は入力を複数のモ デルの 1 つに振り分ける方法である木構造モデルを扱う. 木構造モデルのでは,入力空間を矩形 (cuboid) 領域に分けて,それぞ れの領域に対応するモデルに予測をさせる. A B C D E θ1 θ4 θ2 θ3 x1 x2 x1 > θ1 x2 > θ3 x1 θ4 x2 θ2 A B C D E
- 27. 27/50 CART 以下では木構造モデルの 1 つである CART (classi?cation and regression tree) を扱う.CART は名前の通り分類にも回帰にも使う ことができるが,まずは回帰に絞って説明する. 入力と目標値の組 D = (x1, tn) , . . . , (xN , tN ) ∈ RD × R が与えられて いるとする.入力に対する分割が R1, . . . , RM となっているとき,予測 値を次のように定義する. f (x) := M m=1 cm1Rm (x)
- 29. 29/50 分割が与えられているときの最適な予測値 各領域で二乗和誤差を最小化する予測値を求めよう. Im := {n ; xn ∈ Rm} と表すと誤差は以下のようになる. N n=1 (tn ? f (xn)) 2 = N n=1 tn ? M m=1 cm1Rm (xn) 2 = M m=1 n∈Im (cm ? tn) 2 各 cm について微分して 0 と置くと,最適な予測値は ?cm = 1 |Im| n∈Im tn となることが分かる.ただし二乗和誤差を最小化するような分割を決め ようとすると計算量が大きくなる.そこで貪欲法を使って木の構造を定 める.
- 30. 30/50 分割基準 各回の領域の分割基準を考える.変数を表す添字を j ∈ {1, . . . , D},閾 値を θ として,2 つの領域 R1 (j, θ) と R2 (j, θ) を次で定める. R1 (j, θ) = {x ; xj ≤ θ} , R2 (j, θ) = {x ; xj > θ} Ii (j, θ) := {n ; xn ∈ Ri (j, θ)} とする.分割の基準となる (j, θ) は次を 解いて得られる. min j∈{1,...,D} min θ ? ? ? min c1 n∈I1(j,θ) (c1 ? tn) 2 + min c2 n∈I2(j,θ) (c2 ? tn) 2 ? ? ? . 内側の和を最小化する c1 と c2 は,それぞれ ?c1 = 1 |I1 (j, θ)| n∈I1(j,θ) tn, ?c2 = 1 |I2 (j, θ)| n∈I2(j,θ) tn となる.あとは各 j について最適な θ を計算し,そのあとで最適な j を 求めればよい.
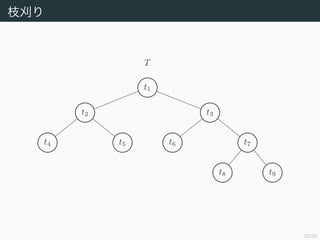
- 32. 32/50 枝刈り T t1 t2 t3 t4 t5 t6 t7 t8 t9
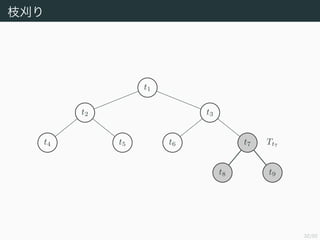
- 33. 32/50 枝刈り t1 t2 t3 t4 t5 t6 Tt7t7 t8 t9
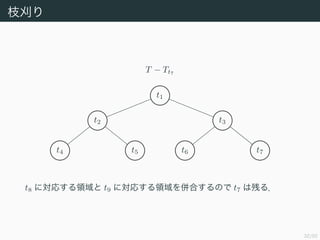
- 34. 32/50 枝刈り T ? Tt7 t1 t2 t3 t4 t5 t6 t7 t8 に対応する領域と t9 に対応する領域を併合するので t7 は残る.
- 35. 33/50 枝刈りの基準 切り落とす位置は,次の error-complexity measure Rα (T) = R (T) + α T が一番大きく減少するような節点 t を選ぶ.ただし T は木 T の葉全体 の集合,R (T) は誤差 R (T) := T m=1 n∈Im (?cm ? tn) 2 である.α ≥ 0 は枝の数に対する罰則を調整するパラメータである.こ の基準では,刈っても(通常大きくなってしまう)誤差があまり大きく ならず,葉の数が減るような枝刈りが優先して行われる.
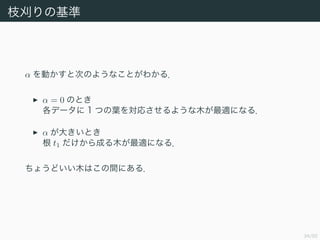
- 36. 34/50 枝刈りの基準 α を動かすと次のようなことがわかる. α = 0 のとき 各データに 1 つの葉を対応させるような木が最適になる. α が大きいとき 根 t1 だけから成る木が最適になる. ちょうどいい木はこの間にある.
- 37. 35/50 枝刈り 部分木 Tt と節点 t から下を刈ってできる木 ({t} , ?) の error-complexity measure はそれぞれ Rα (Tt) = R (Tt) + α Tt , Rα (({t} , ?)) = R (({t} , ?)) + α である.Rα (Tt) > Rα(({t} , ?)),すなわち α < R (Tt) ? R (({t} , ?)) Tt ? 1 が成り立つならば刈り取ったほうがよい.この右辺を刈り取る効果の指 標とし g (t ; T) := R (Tt) ? R (({t} , ?)) Tt ? 1 と定める.
- 38. 36/50 枝刈り 次の最弱リンク枝刈り (weakest link pruning) と呼ばれるアルゴリズ ムにより T0 · · · TJ = ({t1} , ?) と狭義単調増加列 α0 < · · · < αJ を得る. 1: i ← 0 2: while Ti > 1 3: αi ← min t∈V (T i)T i g t ; Ti 4: T i ← arg min t∈V (T i)T i g t ; Ti 5: for t ∈ T i 6: Ti ← Ti ? Ti t 7: i ← i + 1
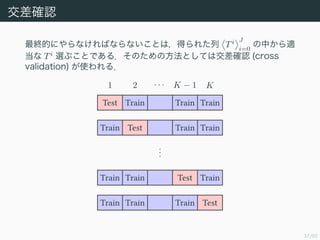
- 39. 37/50 交差確認 最終的にやらなければならないことは,得られた列 Ti J i=0 の中から適 当な Ti 選ぶことである.そのための方法としては交差確認 (cross validation) が使われる. Test Train Train Train Train Test Train Train ... Train Train Test Train Train Train Train Test 1 2 · · · K ? 1 K
- 40. 38/50 交差確認 手順は以下のようになる. 1: データ D を使って,木の列 Ti J i=0 とパラメータの列 αi J i=0 を 作る. 2: データ D を D = K k=1 Dk と分割する.極力,各 |Dk| が同じ大きさ になるようにする. 3: 各 D(k) := DDk を使い,木の列 T(k)i ik i=0 とパラメータの列 α (k) i ik i=0 を作る.
- 41. 39/50 交差確認 4: 各 αi := √ αiαi+1 に対して Rαi (T) を最小化するような T(1) (αi) , . . . , T(K) (αi) とそれらに対応する予測 y (1) i , . . . , y (K) i を求 める.ここで α ∈ α (k) i , α (k) i+1 ならば T(k) (α) = T(k)i となること に注意する. 5: 今までの結果から以下を求めることができる. RCV Ti = 1 N K k=1 n∈{n ; (xn,tn)∈Dk} tn ? y (k) i (xn) 2 6: 誤差が一番小さい木を T?? := arg minT i R Ti とする.
- 42. 40/50 交差確認 7: 標準誤差 (standard error) SE を求める. SE RCV Ti := s Ti / √ N, s Ti := 1 N N n=1 tn ? y (κ(n)) i (xn) 2 ? RCV (Ti) 2 , κ (n) = K k=1 k1Dk ((xn, tn)) 8: 以下を満たす T の中で最小の木 T? を最終的な結果とする. RCV (T) ≤ RCV (T?? ) + 1 × SE (T?? ) このヒューリスティックな決め方は 1 SE rule と呼ばれる.
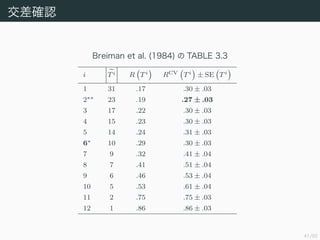
- 43. 41/50 交差確認 Breiman et al. (1984) の TABLE 3.3 i Ti R Ti RCV Ti ± SE Ti 1 31 .17 .30 ± .03 2?? 23 .19 .27 ± .03 3 17 .22 .30 ± .03 4 15 .23 .30 ± .03 5 14 .24 .31 ± .03 6? 10 .29 .30 ± .03 7 9 .32 .41 ± .04 8 7 .41 .51 ± .04 9 6 .46 .53 ± .04 10 5 .53 .61 ± .04 11 2 .75 .75 ± .03 12 1 .86 .86 ± .03
- 44. 42/50 CART による分類 次に分類を扱う.手順は回帰とほぼ同様なので,分割の基準だけ扱う. C1, . . . , CK の K クラスに分類する問題を解きたいとする.節点 t を 通って流れていくデータの数を N (t) とする.またそれらのうちで Ck に属するものの数を Nk (t) と表す.このとき p (t|Ck) = Nk (t) Nk , p (Ck, t) = p (Ck) p (t|Ck) = Nk N Nk (t) Nk = Nk (t) N , p (t) = K k=1 p (Ck, t) = N (t) N である.よって事後確率 p (Ck|t) は次のように求められる. p (Ck|t) = p (Ck, t) p (t) = Nk (t) N (t)
- 45. 43/50 CART による分類 分割の基準には不純度関数 (impurity function) というものを使う.不 純度関数とは,以下の条件を満たす関数 ? : ?M → R のことである. 1. ? (p) は p = (1/M, · · · , 1/M) のときに限り最大となる. 2. ? (p) は p = (0, · · · , 0, i 1, 0, · · · , 0) のときに限り最小となる. 3. ?(p1, . . . , i pi, . . . , j pj, . . . , pM ) = ?(p1, . . . , i pj, . . . , j pi, . . . , pM ).
- 46. 44/50 不純度 不純度関数を ? とすると,任意の節点 t の不純度 I (t) は I (t) := ? (p (C1|t) , . . . , p (CK|t)) で定められる. 節点 t の子 tL と tR について,t からそれらに流れるデータの割合を pL = p (tL) p (t) , pR = p (tR) p (t) とすると,t において基準 s で分割したときの不純度の減少は ?I (s, t) = I (t) ? pRI (tR) ? pLI (tL) と表される.不純度の減少が最大になるような分割を行っていけばよい.
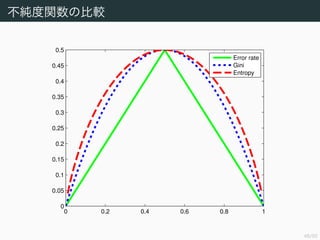
- 47. 45/50 不純度関数の例 誤分類率 I (t) = 1 ? max k p (Ck|t) 交差エントロピー I (t) = ? K k=1 p (Ck|t) log p (Ck|t) ジニ指数 (Gini index) I (t) = K k=1 p (Ck|t) (1 ? p (Ck|t))
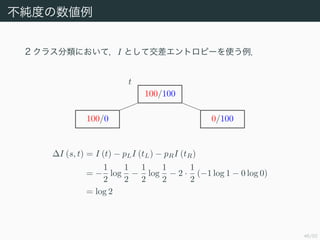
- 48. 46/50 不純度の数値例 2 クラス分類において,I として交差エントロピーを使う例. t 100/100 100/0 0/100 ?I (s, t) = I (t) ? pLI (tL) ? pRI (tR) = ? 1 2 log 1 2 ? 1 2 log 1 2 ? 2 · 1 2 (?1 log 1 ? 0 log 0) = log 2
- 49. 47/50 不純度の数値例 別な分割 s を使う例. t 100/100 60/40 40/60 ?I (s , t) = I (t) ? pLI (tL) ? pRI (tR) = log 2 ? 2 · 1 2 ? 3 5 log 3 5 ? 2 5 log 2 5 < ?I (s, t) 前の分割 s のほうが好ましい.
- 50. 48/50 不純度関数の比較 0 0.2 0.4 0.6 0.8 1 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 Error rate Gini Entropy
- 52. 50/50 参考文献 Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer. Breiman, L., Friedman, J., Stone, C. J., and Olshen, R. A. (1984). Classi?cation and regression trees. CRC press. Freund, Y. and Schapire, R. E. (1996). Experiments with a new boosting algorithm. Friedman, J., Hastie, T., Tibshirani, R., et al. (2000). Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors). The annals of statistics. Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Elements of Statistical Learning: data mining, inference and prediction. Springer, second edition. Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. 平井有三 (2012). はじめてのパターン認識. 森北出版.







![12/50
バギングの誤差評価
特に誤差の平均が 0 で無相関である,すなわち
E [εm (x)] = 0 (14.12)
cov (εm (x) , ε (x)) = E [εm (x) ε (x)] = 0, m = (14.13)
が成り立つならば 1
ECOM = E
?
? 1
M
M
m=1
εm (x)
2
?
?
=
1
M2
E
M
m=1
(εm (x))
2
=
1
M
EAV (14.14)
となり,誤差の期待値が大幅に低減される.
1 同じようなモデルを,同じような訓練データで学習させているのだから,こんなことは
期待できない.](https://image.slidesharecdn.com/prml14-150925085543-lva1-app6892/85/PRML-14-12-320.jpg)






![22/50
ブースティングのための誤差関数
以下の指数誤差を考える.
E [exp (?ty (x))] =
t∈{?1,1}
exp (?ty (x)) p (t|x) p (x) dx (14.27)
変分法を使って y について上式を最小化する.
?t (y) := exp (?ty (x)) p (t|x) p (x) とする.停留点は以下のように求め
られる.
t∈{?1,1}
Dy?t (y) = 0
exp (y (x)) p (t = ?1|x) ? exp (?y (x)) p (t = 1|x) = 0
y (x) =
1
2
log
p (t = 1|x)
p (t = ?1|x)
(14.28)
つまり AdaBoost は逐次的に p (t = 1|x) と (t = ?1|x) の比の対数の近
似を求めている.これが最終的に (14.19) で符号関数を使って分類器を
作った理由となっている.](https://image.slidesharecdn.com/prml14-150925085543-lva1-app6892/85/PRML-14-22-320.jpg)