More Related Content Viewers also liked (13)
PPTX
Conic Sections- Circle, Parabola, Ellipse, Hyperbola
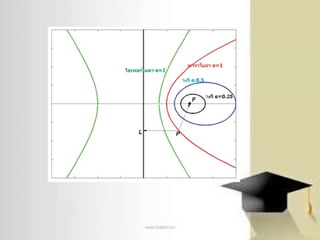
Naman Kumar
Similar to ภาคตัดกรวย (20)
PDF
Student-pilot-handbook-by-tutor ferry (Ex)
Tutor Ferry
PDF
ประมวลรายวิชา คณิตศาสตร์เพิ่มเติม2 ค31202
Aun Wny
More from guest00db6d99 (13) 2. ภาคตัดกรวย ( conic section หรือ conic) ในทางคณิตศาสตร์ หมายถึง เส้นโค้ง ที่ได้จากการตัด พื้นผิวกรวย กลม ด้วย ระนาบ แบน ภาคตัดกรวยนี้ถูกตั้งเป็นหัวข้อศึกษาตั้งแต่สมัย 200 ปีก่อนคริสต์ศักราชโดย อพอลโลเนียส แห่ง เพอร์ กา ผู้ซึ่งศึกษาภาคตัดกรวยและค้นพบสมบัติหลายประการของภาคตัดกรวย ต่อมากรณีการศึกษาภาคตัดกรวยถูกนำไปใช้ประโยชน์หลายแบบ ได้แก่ ในปี พ . ศ . 2133 ( ค . ศ . 1590) กาลิเลโอ กาลิเลอี พบว่าขีปนาวุธที่ยิงขึ้นไปในมุมที่กำหนดมีวิถีการเคลื่อนที่โค้งแบบพาราโบลา , ใน พ . ศ . 2152 ( ค . ศ . 1609) โยฮันส์ เคปเลอร์ พบว่าวงโคจรของดาวเคราะห์รอบนอกเป็นรูปวงรี เป็นต้น 3. ชนิดของภาคตัึϸรวย วงกลม และ วงรี คือ เส้นโค้งซึ่งได้จากการตัดกรวย ด้วยระนาบ ให้ได้ เส้นโค้งปิด ( เป็นวง ) วงกลมนั้นถือเป็นกรณีพิเศษของวงรี โดยแนวของระนาบในการตัดนั้น ตั้งฉากกับแกนกลางของกรวย หากระนาบตัดกรวยในแนวขนานกับเส้นขอบของกรวย หรือเรียก เส้นกำเนิดกรวย ( generator line) จะได้เส้นโค้งเรียกว่า พาราโบลา หากระนาบไม่อยู่ในแนวขนานเส้นขอบ และตัด กรวยได้เส้นโค้งเปิดไม่เป็นวง จะเรียกเส้นโค้งนี้ว่า ไฮเพอร์โบลา จะเห็นได้ว่าในกรณีนี้ระนาบจะตัดกรวยทั้งครึ่งบน และครึ่งล่าง ได้เป็นเส้นโค้งที่ขาดจากกันสองเส้น ในกรณีที่เรียกว่าในภาษาอังกฤษว่า ดีเจนเนอเรต ระนาบจะตัดผ่านจุดยอดของกรวย และได้ผลของการตัดเป็น จุด เส้นตรง หรือ เส้นตรงสองเส้นตัดกัน กรณีเหล่านี้ไม่ได้ถูกรวมไว้ในภาคตัดกรวย 4. ภาคตัดกรวยจากทางึϸȨองจุด แต่ละประเภทของภาคตัดกรวยนั้น สามารถนิยามโดยการใช้เส้นทางเดินของจุด โดยทุก ๆ จุด P บนเส้นทางเดิน จะต้องเป็นไปตามคุณสมบัติเฉพาะดังนี้ 5. วงกลม : ระยะ ( P,C ) = r โดยที่ C คือจุดตายตัวเรียกว่า จุดศูนย์กลาง และ r คือค่าคงที่ เรียกว่า รัศมี พาราโบลา : ระยะ ( P,F ) = ระยะ ( P,L ) โดยที่ F คือจุดตายตัว เรียกว่า จุดโฟกัส และ L คือ เส้นตรง กำหนดตายตัว และไม่ผ่านจุดโฟกัส เรียกว่า ไดเรกทริกซ์ วงรี : ระยะ ( P,A ) + ระยะ ( P,B ) = d โดยที่ A , B เป็นจุดตายตัวสองจุดที่แตกต่างกัน เรียกว่า จุดโฟกัส และ d เป็นค่าคงที่ ที่มีค่ามากกว่า ระยะ ( A,B ) เรียกว่า เส้นผ่านศูนย์กลางหลัก ไฮเพอร์โบลา : ระยะ ( P,A ) - ระยะ ( P,B ) = d โดยที่ A , B เป็นจุดตายตัวสองจุดที่แตกต่างกัน เรียกว่า จุดโฟกัส และ d เป็นค่าคงที่ ที่มีค่าน้อยกว่า ระยะ ( A 6. ความเยื้อง ( Eccentricity) ค่าความเยื้อง หรือ ค่าความเบี่ยงเบนจากศูนย์กลาง ( eccentricity) ของภาคตัดกรวย เป็นค่าบ่งชี้ถึงความเบี้ยว หรือ เบี่ยงเบนไปจากความกลม โดยเมื่อความเยื้องมีค่าลดลง รูปร่างของภาคตัดกรวยที่ได้จะมีรูปร่างเข้าใกล้ทรงกลมมากขึ้น ถ้าเส้นตรง L คือไดเรกทริกซ์ และ F คือ จุดโฟกัส ค่าความเยื้อง หาได้จาก 7. คือ ระยะทางจากจุด ใดๆ บนภาคตัดกรวย ไปยังจุดโฟกัส คือ ระยะทางจากจุด ใดๆ บนภาคตัดกรวย ไปตั้งฉากกับไดเรกทริกซ์ รูปร่างของภาคตัดกรวยที่ได้ ขึ้นกับค่า โดย เป็นรูปวงรี เป็นรูปพาราโบลา เป็นรูปไฮเพอร์โบลา โดยที่ 9. ภาคตัดกรวยกับเรྺาคณิตวิเคราะห์ บน ระบบพิกัด คาร์ ทีเซียน กราฟของสมการสองตัวแปร กำลังสอง ( quadratic equation) จะเป็นรูปภาคตัดกรวยเสมอ หากเราพิจารณาสมการที่อยู่ในรูป ถ้า h 2 = ab แล้ว จะได้สมการของรูป พาราโบลา ถ้า h 2 < ab และ a b และ / หรือ h 0 แล้ว จะได้สมการของรูป วงรี ถ้า h 2 > ab แล้ว จะได้สมการของรูป ไฮเพอร์โบลา ถ้า h 2 < ab and a = b and h = 0 แล้ว จะได้สมการของรูป วงกลม ถ้า a + b = 0 แล้ว จะได้สมการของรูป ไฮเพอร์โบลามุมฉาก แล้ว : 11. เซมิเลตัสเรกตัม และ ระบบพิกัดเชิงขั้ว เซมิเลตัสเรกตัม ของภาคตัดกรวย ปกติเขียนแทนด้วย l คือ ระยะทางจากจุดโฟกัสหนึ่ง ไปยังภาคตัดกรวย โดยวัดตั้งฉากกับแกนหลัก ( major axis ) มีความสัมพันธ์กับ a และ b โดย หรือ ใน ระบบพิกัดเชิงขั้ว นั้น ภาคตัดกรวยที่มีจุดโฟกัสหนึ่งอยู่ที่จุดออริจิน และอีกจุดหนึ่ง ( หากมี ) บนแกน x ด้านบวก จะกำหนดโดยสมการต่อไปนี้ 13. คุณสมบัติทั่วไป ภาคตัดกรวยนั้นมีรูปร่างที่มนสม่ำเสมอ ไม่มี จุดเปลี่ยนโค้ง ( inflection point) ซึ่งเป็นคุณสมบัติที่มีความสำคัญต่อการใช้งานหลายประเภท เช่น การใช้งานเกี่ยวกับ แอโรไดนามิกส์ ซึ่งพื้นผิวนั้นจำเป็นต้องออกแบบเพื่อให้ของไหล ไหลผ่านอย่างสม่ำเสมอ ( laminar flow) เพื่อป้องกันการเกิด การไหลทะลัก ( turbulence) 14. การประยุกต์ใช้งาน ภาคตัดกรวยนั้นได้มีความสำคัญต่อ ดาราศาสตร์ โดย วงโคจรของวัตถุสองชิ้นซึ่งมี แรงดึงดูด กระทำต่อกัน ตามกฏของ นิว ตัน นั้นจะมีรูปร่างเป็นภาคตัดกรวย หาก จุดศูนย์กลางมวล ( center of mass) ร่วมของทั้งสองวัตถุนั้นอยู่นิ่ง หากทั้งสองนั้นถูกดึงดูดอยู่ด้วยกัน ทางเดินของทั้งสองนั้นจะเป็นรูปวงรี หากวัตถุทั้งสองวิ่งออกจากกัน ทางเดินจะเป็นรูปพาราโบลา หรือ ไฮเปอร์โบลา ดู ปัญหาวัตถุ N ชิ้น 15. ใน เรขาคณิตเชิงภาพฉาย ( projective geometry) นั้น ภาพฉายบนระนาบ ของภาคตัดกรวยแต่ละชนิดนั้นจะเหมือนกัน ขึ้นอยู่กับลักษณะการฉาย หรือที่เรียกว่า การแปลงเชิงภาพฉาย ( projective transformation) สำหรับการประยุกต์ใช้งานเฉพาะของภาคตัดกรวยแต่ละชนิดนั้น ดูที่บทความ วงกลม วงรี พาราโบลา ไฮเพอร์โบลา 
