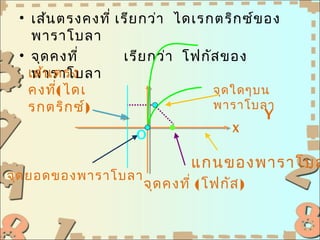
аё аёІаё„аё•аёұаё”аёҒаёЈаё§аёў
- 1. аё аёІ аё„ аё•аёұаё”аёҒ аёЈаё§аёў аёһаёІаёЈаёІа№ӮаёҡаёҘаёІ (parabola)
- 2. аёҡаё—аёҷаёҙаёўаёІаёЎ вҖў аёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё„аё·аёӯ а№ҖаёӢаё•аёӮаёӯаёҮаёҲаёёаё”аё—аёёаёҒаёҲаёёаё” аёҡаёҷаёЈаё°аёҷаёІаёҡ аёӢаё¶а№ҲаёҮаёӯаёўаё№а№Ҳаё«а№ҲаёІаёҮаёҲаёІаёҒа№ҖаёӘа№үаёҷаё•аёЈаёҮаё—аёөа№Ҳ а№ҖаёӘа№үаёҷаё«аёҷаё¶а№ҲаёҮаёҡаёҷаёЈаё°аёҷаёІаёҡа№ҒаёҘаё°аёҲаёёаё”аё„аёҮаё—аёөа№ҲаёҲаёёаё” аё«аёҷаё¶а№ҲаёҮаёҡаёҷаёЈаё°аёҷаёІаёҡаёҷаёӯаёҒа№ҖаёӘа№үаёҷаё•аёЈаёҮаё„аёҮаё—аёөа№Ҳаёҷаёұа№үаёҷ а№Җаёӣа№ҮаёҷаёЈаё°аёўаё°аё—аёІаёҮа№Җаё—а№ҲаёІаёҒаёұаёҷа№ҖаёӘаёЎаёӯ
- 3. а№ҖаёҘаё•аёұаёӘ а№ҖаёЈаёҒаё•аёұаёЎ вҖў а№ҖаёҘаё•аёұаёӘ а№ҖаёЈаёҒаё•аёұаёЎ ( latus rectum ) аё„аё·аёӯ аё„аёӯаёЈа№Ңаё” аё—аёөа№Ҳ аё•аёұа№үаёҮ аёүаёІаёҒаёҒаёұаёҡ а№ҒаёҒаёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҒаёҘаё°аёңа№ҲаёІ аёҷ а№ӮаёҹаёҒаёұаёӘ аёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ ( аёӘа№Ҳаё§ аёҷаёӮаёӯаёҮа№ҖаёӘа№үаёҷ аё•аёЈаёҮаё—аёөа№ҲаёЎ аёөаёҲ аёёаё” аёӣаёҘаёІаёўаёӯаёўаё№аёҡ аёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ а№Ҳ а№ҖаёЈаёөаёў аёҒаёҒаё§а№ҲаёІ аё„аёӯаёЈа№Ңаё” (chord)аёӮаёӯаёҮ аёһаёІаёЈаёІа№ӮаёҡаёҘаёІ ) аё„аё§аёІаёЎаёўаёІаё§аёӮаёӯаёҮа№ҖаёҘаё•аёұ аёӘа№ҖаёЈаёҒаё•аёұаёЎ а№ғаёҠа№үаё§аёЎаёөаё„вҖңаё„аё§аёІаёЎ аёҒаё§а№үаёІ аёІ аёҒаёұаёҡаёӮаёӯаёҮ а№ҖаёҘаё•аёұаёӘ а№ҖаёЈаёҒаё•аёұаёЎ аёұаё” аё§аёІаёЎаёўаёІаё§а№Җаё—а№Ҳ аёҮ вҖқ 4c аёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё«аёҷа№Ҳаё§ аёў
- 4. вҖў а№ҖаёӘа№үаёҷ аё•аёЈаёҮаё„аёҮаё—аёөа№Ҳ а№ҖаёЈаёөаёў аёҒаё§а№ҲаёІ ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒ аёӢа№ҢаёӮ аёӯаёҮ аёһаёІаёЈаёІа№ӮаёҡаёҘаёІ вҖў аёҲаёёаё” аё„аёҮаё—аёөа№Ҳ а№ҖаёЈаёөаёў аёҒаё§а№ҲаёІ а№ӮаёҹаёҒаёұаёӘ аёӮаёӯаёҮ а№ҖаёӘа№үаёҷ аё•аёЈаёҮ аёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё„аёҮаё—аёөа№Ҳ( ไดа№Җ аёҲаёёаё” а№ғаё”а№Ҷаёҡаёҷ аёЈаёҒаё•аёЈаёҙаёҒ аёӢа№Ң) аёһаёІаёЈаёІа№ӮаёҡаёҘаёІ Y X O а№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘ аёҲаёёаё” аёўаёӯаё”аёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аёҲаёёаё” аё„аёҮаё—аёөа№Ҳ (а№ӮаёҹаёҒаёұаёӘ )
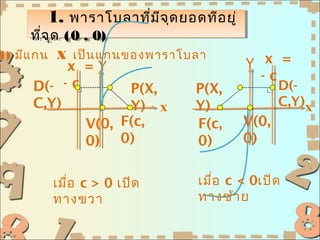
- 5. 1. аёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё—аёөа№ҲаёЎ аёҲ аёёаё” аёўаёӯаё”аё—аёөаёӯ аёўаё№а№Ҳ а№Ҳ 1. аёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё—аёөа№ҲаёЎаёө аёөаёҲ аёёаё” аёўаёӯаё”аё—аёөаёӯ аёўаё№ аё—аёөа№ҲаёҲ аёёаё” (0 ,, 0) аё—аёөа№ҲаёҲ аёёаё” (0 0) 1) аёЎаёөа№Ғ аёҒаёҷ X а№Җаёӣа№Үаёҷ а№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ x =Y Y x = -c D(- - c P(X, P(X, D(- C,Y) Y) Y) C,Y) V(0, F(c, F(c, V(0, 0) 0) 0) 0) а№ҖаёЎаё·а№Ҳаёӯ c > 0 а№Җаёӣаёҙаё” а№ҖаёЎаё·а№Ҳаёӯ c < 0а№Җаёӣаёҙаё” аё—аёІаёҮаёӮаё§аёІ аё—аёІаёҮаёӢа№үаёІ аёў
- 6. вҖў аёҒаёіаёІаё«аёҷаё”а№ғаё«а№ү P(x, y) а№Җаёӣа№ҮаёҷаёҲаёёаё”а№ғаё”а№ҶаёҡаёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ а№ҒаёҘаё° PD аё•аёұа№үаёҮаёүаёІаёҒаёҒаёұаёҡไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒаёӢа№Ңаё—аёөа№ҲаёҲаёёаё” D(x, вҖ“c) аёҲаёІаёҒаёҡаё—аёҷаёҙаёўаёІаёЎаёҲะไดа№ү PF = PD аёўаёҒаёҒаёіаёІаёҘаёұаёҮаёӘаёӯаёҮаё—аёұа№үаёҮаёӘаёӯаёҮаёӮа№үаёІаёҮаёҲะไดа№ү аё”аёұаёҮаёҷаёұаёҷ а№ү
- 7. аёҷаёұа№Ҳаёҷ аё„аё·аёӯ аёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ x 2 = 4cy аёҲаёёаё”аёўаёӯаё”аёӯаёўаё№а№Ҳаё—аёөа№ҲаёҲаёёаё”(0, 0) аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёөа№ҲаёҲаёёаё”(0, c) ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒаёӢа№Ңаё„аё·аёӯ а№ҖаёӘа№үаёҷаё•аёЈаёҮ y = вҖ“ c а№ҒаёҘаё°аёЎаёөа№ҒаёҒаёҷ Y а№Җаёӣа№Үаёҷа№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё–а№үаёІ c > 0 а№ҒаёҘа№үаё§ x2= 4cy а№Җаёӣа№ҮаёҷаёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё—аёөа№ҲаёЎаёөаёҒаёЈаёІаёҹаё«аёҮаёІаёўаёӮаё¶а№үаёҷ аё–а№үаёІ c < 0 а№ҒаёҘа№үаё§ x2= 4cy а№Җаёӣа№ҮаёҷаёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё—аёөа№ҲаёЎаёөаёҒаёЈаёІаёҹаё„аё§аёіа№ҲаёІаёҘаёҮ
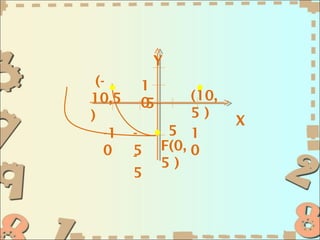
- 8. аё•аёұаё§аёӯаёўа№ҲаёІаёҮаё—аёөа№Ҳ 1 аёҲаёҮаё«аёІаёӘаёЎаёӮаёӯаёҮаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аёҲаёІаёҒаёӘаёҙа№ҲаёҮаё—аёөа№Ҳ аёҒаёіаёІаё«аёҷаё”а№ғаё«а№үаё”аёұаёҮаё•а№Ҳаёӯไаёӣаёҷаёөа№ү (1) аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёөа№Ҳ (0, 5) а№ҒаёҘаё°аёҲаёёаё”аёўаёӯаё”аёӯаёўаё№аё—аёөа№Ҳ (0, 0) а№Ҳ аёҲаёІаёҒа№ӮаёҲаё—аёўа№Ң аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёөа№Ҳ (0, 5) а№ҒаёҘаё°аёҲаёёаё”аёўаёӯаё”аёӯаёўаё№аё—аёөа№Ҳ (0, 0) а№Ҳ а№ҒаёӘаё”аёҮаё§а№ҲаёІа№ҒаёҒаёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё„аё·аёӯ а№ҒаёҒаёҷ Y (а№ҖаёӘа№үаёҷаё•аёЈаёҮ x = 0) c = 5 а№Җаёӣа№ҮаёҷаёҒаёЈаёІаёҹаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё«аёҮаёІаёў аёӮаё¶а№үаёҷ ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒаёӢа№Ңаё„аё·аёӯа№ҖаёӘа№үаёҷаё•аёЈаёҮ y = вҖ“5 аёҘаёІаё•аёұаёӘа№ҖаёЈаёҒаё•аёұаёЎаёўаёІаё§а№Җаё—а№ҲаёІаёҒаёұаёҡ | 4(5) | = 20 аё«аёҷа№Ҳаё§аёў аёӘаёЎаёҒаёІаёЈаёӯаёўаё№а№ғаёҷаёЈаё№аёӣ x2= 4cy а№Ҳ аёҲะไดа№үаёӘаёЎаёҒаёІаёЈ x2= 4(5)y
- 9. Y (- 1 10,5 0 (10, 5 ) 5) X -1 - 5 1 0 5 F(0, 0 - 5) 5
- 10. 2) аёЎаёөа№Ғ аёҒаёҷ Y а№Җаёӣа№Үаёҷ а№ҒаёҒаёҷаёӮаёӯаёҮ аёһаёІаёЈаёІа№ӮаёҡаёҘаёІ Y Y y = D(x, F(0, -c -c) c) P(x, X P(x,X V(0, y) V(0 y = y) 0) D(x,-c) ,0) F(0,c -c ) а№ҖаёЎаё·а№Ҳаёӯ c > 0 аё«аёҮаёІаёў а№ҖаёЎаё·а№Ҳаёӯ c < 0 аёӮаё¶а№үаёҷ аё„аё§аёіа№ҲаёІ аёҘаёҮ
- 11. вҖў аёҒаёіаёІаё«аёҷаё”а№ғаё«а№ү P(x, y) а№Җаёӣа№ҮаёҷаёҲаёёаё”а№ғаё”а№ҶаёҡаёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ а№ҒаёҘаё° PD аё•аёұа№үаёҮаёүаёІаёҒаёҒаёұаёҡไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒаёӢа№Ңаё—аёөа№ҲаёҲаёёаё” D(вҖ“ c, y) аёўаёҒаёҒаёіаёІаёҘаёұаёҮаёӘаёӯаёҮаё—аёұа№үаёҮаёӘаёӯаёҮаёӮа№үаёІаёҮ аё”аёұаёҮаёҷаёұа№үаёҷ
- 12. вҖў аёҷаёұа№Ҳаёҷ аё„аё·аёӯ аёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ y2 = 4cx аёҲаёёаё”аёўаёӯаё”аёӯаёўаё№а№Ҳаё—аёҲаёёаё” (0,0) аёөа№Ҳ аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёҲаёёаё” (C,0) аёөа№Ҳ ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒаёӢа№Ңаё„аё·аёӯ а№ҖаёӘа№үаёҷаё•аёЈаёҮ X = -C а№ҒаёҘаё°аёЎаёөа№ҒаёҒаёҷ X а№Җаёӣа№Үаёҷ а№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё–а№үаёІ C>0 а№ҒаёҘа№үаё§ y2 = 4cx а№Җаёӣа№ҮаёҷаёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё—аёөа№ҲаёЎаёөаёҒаёЈаёІаёҹаё—аёІаёҮаёӮаёІаё§ аё–а№үаёІ C<0 а№ҒаёҘа№үаё§ y2 = 4cx а№Җаёӣа№ҮаёҷаёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аё—аёөа№ҲаёЎаёөаёҒаёЈаёІаёҹаё—аёІаёҮаёӢа№үаёІаёў
- 13. аёӮа№үаёӯаёӘаёұаёҮа№ҖаёҒаё• 1) аёЈаё°аёўаё°аё—аёІаёҮаёҲаёІаёҒаёҲаёёаё” аёўаёӯดไаёӣаёўаёұаёҮ а№ӮаёҹаёҒаёұаёӘ а№Җаё—а№ҲаёІ аёҒаёұаёҡ аёЈаё°аёўаё°аё«а№ҲаёІ аёҮ аёЈаё°аё«аё§а№ҲаёІ аёҮаёҲаёёаё” аёўаёӯаё”аёҒаёұаёҡ ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒ аёӢа№Ң 2) а№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаёңа№ҲаёІ аёҷаёҲаёёаё” аёўаёӯаё”а№ҒаёҘаё°а№ӮаёҹаёҒаёұаёӘ 3) а№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№Җаёӣа№Үаёҷ а№ҒаёҒаёҷаёӘаёЎаёЎаёІаё•аёЈ
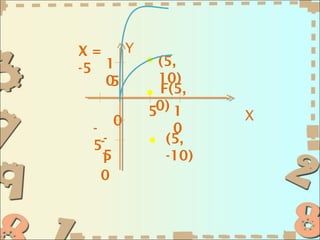
- 14. аё•аёұаё§аёӯаёўа№ҲаёІаёҮаё—аёөа№Ҳ 2 аёҲаёҮаё«аёІаёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аёҲаёІаёҒаёӘаёҙаёҮаё—аёөа№ҲаёҒаёіаёІаё«аёҷаё”а№ғаё«а№ү а№Ҳ аё”аёұаёҮаё•а№Ҳаёӯไаёӣаёҷаёөа№ү (1) аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёөа№Ҳ (5, 0) а№ҒаёҘаё°аёҲаёёаё”аёўаёӯаё”аёӯаёўаё№аё—аёөа№Ҳ (0, 0) а№Ҳ аё§аёҙаёҳаёөаё—аёіаёІ аёҲаёІаёҒа№ӮаёҲаё—аёўа№Ң аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёөа№Ҳ (5, 0) а№ҒаёҘаё°аёҲаёёаё”аёўаёӯаё”аёӯаёўаё№аё—аёөа№Ҳ а№Ҳ (0, 0) а№ҒаёӘаё”аёҮаё§а№ҲаёІа№ҒаёҒаёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё„аё·аёӯ а№ҒаёҒаёҷ X (а№ҖаёӘа№үаёҷаё•аёЈаёҮ y = 0) c = 5 а№Җаёӣа№ҮаёҷаёҒаёЈаёІаёҹаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№Җаёӣаёҙаё”аё—аёІаёҮаёӮаё§аёІ ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒаёӢа№Ңаё„аё·аёӯа№ҖаёӘа№үаёҷаё•аёЈаёҮ x = вҖ“5 аёҘаёІаё•аёұаёӘа№ҖаёЈаёҒаё•аёұаёЎаёўаёІаё§ | 4(5) | = 20 аё«аёҷа№Ҳаё§аёў аёӘаёЎаёҒаёІаёЈаёӯаёўаё№а№Ҳа№ғаёҷаёЈаё№аёӣ y2 = 4cx аёҲะไดа№үаёӘаёЎаёҒаёІаёЈ y2= 4(5)x аё”аёұаёҮаёҷаёұа№үаёҷаёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё—аёөаё•а№үаёӯаёҮаёҒаёІаёЈаё„аё·аёӯ y2= 20x а№Ҳ
- 15. X= Y -5 1 (5, 05 10) F(5, 50) 1 X 0 - 0 5 -- (5, 15 -10) 0
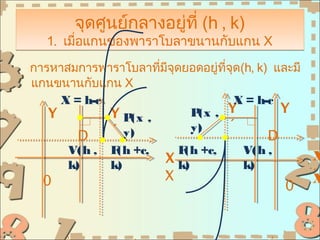
- 16. аёҲаёёаё”аёЁаё№аёҷаёўа№ҢаёҒаёҘаёІаёҮаёӯаёўаё№а№Ҳаё—аёөа№Ҳ (h , k) 1. а№ҖаёЎаё·а№Ҳаёӯа№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаёӮаёҷаёІаёҷаёҒаёұаёҡа№ҒаёҒаёҷ X аёҒаёІаёЈаё«аёІаёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё—аёөаёЎаёҲаёёаё”аёўаёӯаё”аёӯаёўаё№а№Ҳаё—аёҲаёёаё”(h, k) а№ҒаёҘаё°аёЎаёө а№Ҳ аёө аёөа№Ҳ а№ҒаёҒаёҷаёӮаёҷаёІаёҷаёҒаёұаёҡа№ҒаёҒаёҷ X X = h-c X = h-c Y Y P(x , P , Y (x Y Вҙ y) y) Вҙ D D V(h , F +c, (h F +c, (h V(h , X k) X k) k) k) Вҙ X Вҙ X 0 0
- 17. аёҒаёіаёІаё«аёҷаё”а№ғаё«а№ү V(h, k) а№Җаёӣа№ҮаёҷаёҲаёёаё”аёўаёӯаё” а№ҒаёҘаё° аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёөа№Ҳ F(h + c, k) а№ҖаёЎаё·аёӯа№ҖаёҘаё·а№Ҳаёӯаёҷа№ҒаёҒаёҷไаёӣаё—аёөаёҲаёёаё” (h, k) аёҲะไดа№үаёҲаёёаё”аёўаёӯаё” а№ҒаёҘаё° а№Ҳ а№Ҳ а№ӮаёҹаёҒаёұаёӘаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҖаёЎаё·аёӯа№Җаё—аёөаёўаёҡаёҒаёұаёҡа№ҒаёҒаёҷа№ғаё«аёЎа№ҲаёЎаёһаёҒаёұаё”а№Җаёӣа№Үаёҷ (0, а№Ҳ аёө аёҙ 0) а№ҒаёҘаё° (c, 0) аё•аёІаёЎаёҘаёіаёІаё”аёұаёҡ вҖў аё–а№үаёІа№ғаё«а№ү P(xВҙ, yВҙ) а№Җаёӣа№ҮаёҷаёһаёҙаёҒаёұаё”аёӮаёӯаёҮаёҲаёёаё”аёҡаёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҖаёЎаё·а№Ҳаёӯ а№Җаё—аёөаёўаёҡаёҒаёұаёҡа№ҒаёҒаёҷа№ғаё«аёЎа№Ҳ аёҲะไดа№үаёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҖаёЎаё·а№Ҳаёӯ а№Җаё—аёөаёўаёҡаёҒаёұаёҡа№ҒаёҒаёҷа№ғаё«аёЎа№Ҳ аё„аё·аёӯ (yВҙ)2= 4cxВҙ а№Ғаё•а№Ҳ yВҙ= y вҖ“ k а№ҒаёҘаё° xВҙ= x вҖ“ h 2 3 аё”аёұаёҮ аёҷаёұаёҷ аёҲะไดа№үаёӘ аёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҖаёЎаё·аёӯ а№Җаё—аёөаёў аёҡ а№ү а№Ҳ аёҒаёұаёҡ а№ҒаёҒаёҷа№Җаё”аёҙаёЎ аё„аё·аёӯ (y вҖ“ k) 2 = 4c(x вҖ“ h)
- 18. аёҷаёұа№Ҳаёҷ аё„аё·аёӯ аёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ (y вҖ“ k) 2= 4c(x вҖ“ h) аёЎаёөаёҲ аёёаё” аёўаёӯаё”аёӯаёўаё№а№Ҳаё— аёөа№Ҳ (h, k) а№ӮаёҹаёҒаёұаёӘ аёӯаёўаё№а№Ҳаё— аёөа№ҲаёҲ аёёаё” (h +c, k) ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒ аёӢа№Ңаё„ аёӯ а№ҖаёӘа№үаёҷ аё•аёЈаёҮ x = h вҖ“ c аё· а№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаёӮаёҷаёІаёҷаёҒаёұаёҡ а№ҒаёҒаёҷ X аёӯаёўаё№а№Ҳ аёҡаёҷа№ҖаёӘа№үаёҷ аё•аёЈаёҮ y = k аё„аё§аёІаёЎаёўаёІаё§аёӮаёӯаёҮаёҘаёІаё•аёұаёӘ а№ҖаёЈаёҒаё•аёұаёЎ (L atus rectum) а№Җаё—а№ҲаёІ аёҒаёұаёҡ |4c | аё«аёҷа№Ҳаё§ аёўа№ҖаёЎаё·аёӯ c > 0 а№Җаёӣа№Үаёҷ аёҒаёЈаёІаёҹ а№Ҳ аёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№Җаёӣаёҙаё” аё—аёІаёҮаёӮаё§аёІ а№ҒаёҘаё° c < 0 а№Җаёӣа№Үаёҷ аёҒаёЈаёІаёҹаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№Җаёӣаёҙаё” аё—аёІаёҮ аёӢа№үаёІ аёў
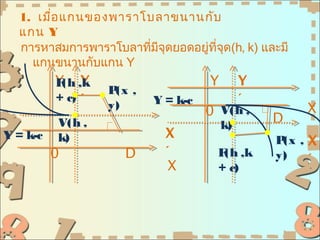
- 19. 1. а№ҖаёЎаё·аёӯ а№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаёӮаёҷаёІаёҷаёҒаёұаёҡ а№Ҳ а№ҒаёҒаёҷ Y аёҒаёІаёЈаё«аёІаёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё—аёөа№ҲаёЎаёҲаёёаё”аёўаёӯаё”аёӯаёўаё№аё—аёҲаёёаё”(h, k) а№ҒаёҘаё°аёЎаёө аёө а№Ҳ аёөа№Ҳ а№ҒаёҒаёҷаёӮаёҷаёІаёҷаёҒаёұаёҡа№ҒаёҒаёҷ Y Y(h ,k F Y Y Y P , (x + c) Вҙ Y = k-c Вҙ y) X 0 V(h , V(h , k) D Y = k-c k) X P ,X (x 0 D Вҙ F ,k (h y) Вҙ X + c)
- 20. аёҒаёіаёІаё«аёҷаё”а№ғаё«а№ү V(h, k) а№Җаёӣа№ҮаёҷаёҲаёёаё”аёўаёӯаё” а№ҒаёҘаё° аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№аё—аёөа№Ҳ F(h , k а№Ҳ + c) а№ҖаёЎаё·аёӯа№ҖаёҘаё·а№Ҳаёӯаёҷа№ҒаёҒаёҷไаёӣаё—аёөаёҲаёёаё” (h, k) аёҲะไดа№үаёҲаёёаё”аёўаёӯаё” а№ҒаёҘаё°а№ӮаёҹаёҒаёұаёӘ а№Ҳ а№Ҳ аёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҖаёЎаё·аёӯа№Җаё—аёөаёўаёҡаёҒаёұаёҡа№ҒаёҒаёҷа№ғаё«аёЎа№ҲаёЎаёһаёҒаёұаё”а№Җаёӣа№Үаёҷ (0, 0) а№Ҳ аёө аёҙ а№ҒаёҘаё° (0, c) аё•аёІаёҘаёіаёІаё”аёұаёҡ вҖў аё–а№үаёІа№ғаё«а№ү P(xВҙ, yВҙ) а№Җаёӣа№ҮаёҷаёһаёҙаёҒаёұаё”аёӮаёӯаёҮаёҲаёёаё”аёҡаёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҖаёЎаё·а№Ҳаёӯ а№Җаё—аёөаёўаёҡаёҒаёұаёҡа№ҒаёҒаёҷа№ғаё«аёЎа№Ҳ аёҲะไดа№үаёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҖаёЎаё·аёӯ а№Ҳ а№Җаё—аёөаёўаёҡаёҒаёұаёҡа№ҒаёҒаёҷа№ғаё«аёЎа№Ҳ аё„аё·аёӯ (xВҙ)2= 4cyВҙ а№Ғаё•а№Ҳ xВҙ= x вҖ“ h а№ҒаёҘаё° yВҙ= y вҖ“ k аё”аёұаёҮ аёҷаёұа№үаёҷ аёҲะไดа№үаёӘ аёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№ҖаёЎаё·аёӯ а№Җаё—аёөаёў аёҡаёҒаёұаёҡ а№ҒаёҒаёҷ а№Ҳ а№Җаё”аёҙаёЎ аё„аё·аёӯ (x вҖ“ h) 2= 4c(y вҖ“ k)
- 21. аёҷаёұа№Ҳаёҷ аё„аё·аёӯ аёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ (x вҖ“ h) 2= 4c(y вҖ“ k) аёЎаёөаёҲ аёёаё” аёўаёӯаё”аёӯаёўаё№аё— аёөа№Ҳ( h, k) а№Ҳ а№ӮаёҹаёҒаёұаёӘ аёӯаёўаё№а№Ҳаё— аёөа№ҲаёҲ аёёаё” (h , k + c) ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒ аёӢа№Ңаё„ аёӯ а№ҖаёӘа№үаёҷ аё•аёЈаёҮ y = k вҖ“ c аё· а№ҒаёҒаёҷаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаёӮаёҷаёІаёҷаёҒаёұаёҡ а№ҒаёҒаёҷ Y аёӯаёўаё№а№Ҳаёҡ аёҷ а№ҖаёӘа№үаёҷ аё•аёЈаёҮ x = h аё„аё§аёІаёЎаёўаёІаё§аёӮаёӯаёҮаёҘаёІаё•аёұаёӘ а№ҖаёЈаёҒаё•аёұаёЎ (L atus rectum) а№Җаё—а№ҲаёІ аёҒаёұаёҡ |4c | аё«аёҷа№Ҳаё§ аёў а№ҖаёЎаё·аёӯ c > 0 а№Җаёӣа№Үаёҷ аёҒаёЈаёІаёҹаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё«аёҮаёІаёўаёӮаё¶а№үаёҷ а№Ҳ а№ҒаёҘаё° c < 0 а№Җаёӣа№Үаёҷ аёҒаёЈаёІаёҹаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё„аё§аёіа№ҲаёІ аёҘаёҮ
- 22. аё•аёұаё§аёӯаёўа№ҲаёІаёҮаё—аёөа№Ҳ 3 аёҲаёҮаё«аёІаёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аёҲаёІаёҒаёӘаёҙа№ҲаёҮаё—аёөа№Ҳ аёҒаёіаёІаё«аёҷаё”а№ғаё«а№үаё”аёұаёҮаё•а№Ҳаёӯไаёӣаёҷаёөа№ү (1) аёҲаёёаё”аёўаёӯаё”аёӯаёўаё№а№Ҳаё—аёөа№Ҳ (вҖ“ 2, 3) а№ҒаёҘаё°аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№аё—аёөа№Ҳ (1, 3) а№Ҳ аё§аёҙаёҳаёөаё—аёіаёІ аёҲаёІаёҒа№ӮаёҲаё—аёўа№Ң аёҲаёёаё”аёўаёӯаё”аёӯаёўаё№аё—аёөа№Ҳ V(вҖ“ 2, 3) = V(h, k) аёҲะไดа№ү а№Ҳ h=вҖ“2, k=3 аёҲаёёаё”а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёөа№Ҳ F(h + c, k) = F(1, 3) аёҲะไดа№ү h + c = 1 аёӢаё¶а№ҲаёҮ вҖ“2 + c = 1 : c = 3 а№ҒаёҒаёҷаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаёӮаёҷаёІаёҷаёҒаёұаёҡ X аё„аё·аёӯ а№ҖаёӘа№үаёҷаё•аёЈаёҮ y = 3 (y = k) ไดа№ҖаёЈаёҒаё•аёЈаёҙаёҒаёӢа№Ңаё„аё·аёӯа№ҖаёӘа№үаёҷаё•аёЈаёҮ x = вҖ“ 5 (x = h вҖ“ c = вҖ“2 вҖ“ 3 = вҖ“ 5) а№Җаёӣа№ҮаёҷаёҒаёЈаёІаёҹаёһаёІаёЈаёІа№ӮаёҡаёҘаёІа№Җаёӣаёҙаё”аё—аёІаёҮаёӮаё§аёІ (c >0) аёҘаёІаё•аёұаёӘа№ҖаёЈаёҒаё•аёұаёЎаёўаёІаё§а№Җаё—а№ҲаёІаёҒаёұаёҡ | 4(3) | = 12 аё«аёҷа№Ҳаё§аёў аёӘаёЎаёҒаёІаёЈаёӯаёўаё№а№Ҳа№ғаёҷаёЈаё№аёӣ (y вҖ“ k)2= 4c(x вҖ“ h)
- 23. y 2вҖ“ 6y + 9 = 12x + 24 y 2вҖ“ 6y вҖ“ 12x вҖ“ 15 = 0 аё”аёұаёҮаёҷаёұаёҷ аёӘаёЎаёҒаёІаёЈаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё—аёөаё•а№үаёӯаёҮаёҒаёІаёЈаё„аё·аёӯ y 2вҖ“ 6y вҖ“ 12x вҖ“ 15 а№ү а№Ҳ = 0 Y Y (1, Вҙ 9) V(- F(1, 2,3) 3) X ВҙX X= F(1,- -5 3)
- 24. аё•аёұаё§аёӯаёўа№ҲаёІаёҮаё—аёөа№Ҳ 4аёҲаёҮаё«аёІаёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІ аёӢаё¶а№ҲаёҮаёЎаёөаёҲаёёаё”аёўаёӯаё”аёӯаёўаё№а№Ҳаё—аёҲF(вҲ’ а№Җаёҷаёҙаё”) аёөа№Ҳ аёёаё”аёҒаёіаёІ 3,0 а№ҒаёҘаё°а№ӮаёҹаёҒаёұаёӘаёӯаёўаё№а№Ҳаё—аёөа№ҲаёҲаёёаё” 2 аё§аёҙаёҳаёөаё—аёіаёІ аёҷаёіаёІаёӘаёҙа№ҲаёҮаё—аёөаёҒаёіаёІаё«аёҷаё”а№ғаё«а№үไаёӣа№ҖаёӮаёөаёўаёҷаёҒаёЈаёІаёҹаё„аёЈа№ҲаёІаё§а№Ҷ а№Җаёһаё·аёӯаё”аё№аё§а№ҲаёІ а№Ҳ а№Ҳ аёҲаёұаё”аёӯаёўаё№а№Ҳа№ғаёҷаёӘаёЎаёҒаёІаёЈа№Ғаёҡаёҡа№ғаё” аёҲаёІаёҒаёҒаёЈаёІаёҹаёҲะไดа№үаёӘаёЎаёҒаёІаёЈ аёһаёІаёЈаёІа№ӮаёҡаёҘаёІаёӯаёўаё№а№ғаёҷаёЈаё№аёӣа№Ҳ y2 = 4cx аёҲаёІаёҒ вҲ’ 2,0 3 F( ) аёҲะไดа№ү вҲ’ 3 = c2 вҲ’2 3 аёҷаёіаёІ c = ไаёӣа№Ғаё—аёҷаё„а№ҲаёІа№ғаёҷаёӘаёЎаёҒаёІаёЈ y2 = 4cx аёҲะไดа№ү вҲ’ 2y2 3 = 4( )x аё”аёұаёҮ аёҷаёұаёҷ аёӘаёЎаёҒаёІаёЈаёӮаёӯаёҮаёһаёІаёЈаёІа№ӮаёҡаёҘаёІаё—аёөа№Ҳไ аё”а№ү аё„аё·аёӯ а№ү y 2 = -6x
- 25. аёӘаёЎаёІаёҠаёҙ аёҒ 1.) аёҷ.аёӘ. аёҒаёёаёҘаёҳаёЈ аёҒаёҘаёіа№үаёІаёҒаёЈаё°а№Ӯаё—аёҒ аёҠаёұаёҷ аёЎ.4/8 а№ҖаёҘаёӮаё—аёөа№Ҳ 11 а№ү 2.) аёҷ.аёӘ. аёҠаёҚаёІаё аёІ аё–аёөаё•аёҙаёӣаёЈаёҙаё§аёұаё•аёЈ аёҠаёұаёҷ аёЎ.4/8 а№ҖаёҘаёӮаё—аёөа№Ҳ 12 а№ү 3.) аёҷ.аёӘ. аёҠаёөаёЈаёІаёһаёЈаёЈаё“ а№ҒаёҒа№ҲаёҷаёҒаёҘаёІаёҮаё”аёӯаёҷ аёҠаёұаёҷ аёЎ.4/8 а№ҖаёҘаёӮ а№ү аё—аёөа№Ҳ 14 4.) аёҷ.аёӘ. аёҳаёұаёҚаёҲаёҙаёЈаёІ аёһаё§аёҮаё—аёӯаёҮ аёҠаёұаёҷ аёЎ.4/8 а№ҖаёҘаёӮаё—аёөа№Ҳ 21 а№ү 5.) аёҷ.аёӘ. аёһаё аёұаёӘаёЈаёІ а№Җаё”аёҠаёӯаёўаё№а№Ҳ аёҠаёұаёҷ аёЎ.4/8 а№ҖаёҘаёӮ а№ү аё—аёөа№Ҳ 32