狠狠撸

确率论基础
@hoxo_m
2016/12/04
1

Watanabe理論勉強会 #7
?? 本資料は
?? Sumio Watanabe, Algebraic Geometry
and Statistical Learning Theory,
Cambridge University Press, 2009.
?? 第7回読書会補?資料です。
2

1.6 Probability Theory
?? この節では確率論の基礎を要約する
?? 確率論に詳しい読者は?ばしてよい
?? 確率論がよく分かっていないので5章に
?る前に復習したい
3

地図
?? 距離空間＝集合＋距離
?? 可測空間＝距離空間＋σ-代数
?? 確率空間＝可測空間＋確率測度
?? 確率変数＝ X: 確率空間 → 可測空間
?? 確率分布 PX
?? 確率変数の期待値 E[X]
?? 確率変数の収束
4

定義1.11 距離空間
?? 集合 Ω
?? 関数 D: Ω ? Ω → R
?? D が距離とは
①? ? x, y ∈ Ω, D(x, y) = D(y, x) ≧ 0
②? D(x, y) = 0 ? x = y
③? ? x, y, z ∈ Ω, D(x, y) + D(y, z) ≧ D(x, z)
?? 距離を持つ集合 Ω を距離空間という
5

位相空間について
?? 距離空間の位相は開近傍によって定まる
–?x の開近傍: Uε = { y ∈ Ω ; D(x, y) < ε }
?? 可分空間: 可算稠密部分集合を持つ TS
?? コーシー列 {xn}:
–?任意の δ > 0 に対して M が存在し
m, n > M ? D(xm, xn) < δ
?? 完備: 全てのコーシー列が収束する
?? ポーランド空間: 完備かつ可分な TS
6

Example 1.8
＜本書で登場する距離空間 3つ＞
(1) 有限次元実ユークリッド空間 Rd
–?距離 D(x, y) = |x – y| = (Σi=1..d(xi – yi)2)?
–?ユークリッドノルム
–?完備かつ可分となる
(2) Rd の部分集合も距離空間
–?有限集合や可算集合を考えることもある
7

Example 1.8 (3)
?? K: Rd のコンパクト部分集合
?? K から Rd’ への連続関数全体の集合
Ω = { f ; f: K → Rd’ }
?? 距離 D(f, g) = maxx∈K | f(x) – g(x) |
?? Ω は距離空間となる
?? K のコンパクト性から Ω は完備かつ可分
8

地図
?? 確率分布 PX
9

定義1.12 (1) 可測空間
?? Ω: 距離空間
?? B: Ω の部分集合を要素とする σ-代数
?? σ-代数(完全加法族):
①? A1, A2 ∈ B ? A1 ∩ A2 ∈ B (※不要)
②? Ω ∈ B (※原?には無いがこちらを追加)
③? A ∈ B ? Ac ∈ B (Ac は補集合)
④? A1, A2, A3, … ∈ B ? ∪Ai ∈ B (可算個)
?? (Ω, B) を可測空間と呼ぶ
10

定義1.12 (2) 確率空間
?? 可測空間 (Ω, B)
?? 確率測度 P
関数 P: B → [0, 1]
①? P(Ω) = 1
②? 交わりの無い A1, A2, A3, … ∈ B に対して
P(∪Ai) = ΣP(Ai)
?? (Ω, B, P) を確率空間と呼ぶ
11

ボレル集合体 (Borel Field)
?? 位相空間 Ω において、全ての開集合を含
む最?の σ-代数をボレル集合体と呼ぶ
12

Remark 1.18
?? 確率空間 (RN, B, P)
?? RN: N次元実ユークリッド空間
?? B: ボレル集合体
?? 確率分布(測度) P を次で定義する(p(x) ≧ 0)
?? p(x) を確率密度関数と呼ぶ
13

地図
?? 確率分布 PX
14

定義1.13 確率変数 (1)
?? 確率空間 (Ω, B, P)
?? 可測空間 (Ω1, B1)
?? 関数 X: Ω → Ω1
?? X が可測であるとき、確率変数と呼ぶ
?? 可測関数：
–?任意の B1 ∈ B1 に対して X-1(B1) ∈ B
?? Ω1-valued 確率変数と呼ばれることも
15

定義1.13 確率変数 (2)
?? 関数 ?(B1) = P(X-1(B1)) は (Ω1, B1) 上の
確率測度である
?? したがって (Ω1, B1, ?) は確率空間となる
?? ? を確率変数 X の確率分布と呼ぶ
?? また、X は ? に従うと?う
?? ? は X の像空間(image space)の確率分布
?? 次と同値
16

Remark 1.9
(1) 確率論では次の簡易表記がよく使われる
?? P( f(x) > 0 ) ≡ P({ ω ∈ Ω; f(X(ω)) > 0 })
?? 定義より
P( f(x) > 0 ) = ?({ x ∈ Ω1; f(x) > 0 })
(2) 確率変数 X が従う確率測度(分布) ? を
PX と表記する
?? ?般に X と PX は?対?ではない
?? 確率分布が定まっても確率変数は定まらない
17

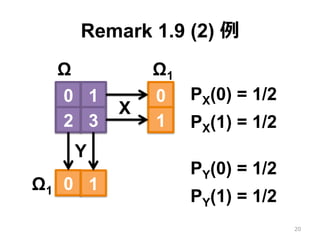
Remark 1.9 (2) 例
?? 確率空間 (Ω, 2Ω, P)
?? Ω = { 0, 1, 2, 3 } (※ 原?では {1,2,3,4})
?? P({i}) = 1/4 ( i = 0, 1, 2, 3 )
?? 次の確率変数 X と Y の確率分布は同じ
?? 確率分布からは X と Y は区別できない
18

Remark 1.9 (2) 例
19
0 1
2 3
0
1
0 1
X
Ω Ω1
Ω1
Y
PX(0) = 1/2
PX(1) = 1/2
PY(0) = 1/2
PY(1) = 1/2

Remark 1.9 (3)
?? 本書の定義や定理の中には、確率変数 X
の像空間 Ω1 と確率分布 PX だけしか必要
がない場合がある
?? このような場合、確率空間 (Ω, B, P) の明
?的な記述は省略される
?? その結果、次のようになる
–?確率分布 PX に従う Ω1-valued 確率変数 X に
対して次の等式が成り?つ???
20

地図
?? 確率分布 PX
21

定義1.14 期待値
?? 確率変数 X: (Ω, B, P) → (Ω1, B1)
?? X は確率分布 PX に従う
?? 期待値:
?? S ? Ω1 の期待値:
22

?? 確率変数 X: (Ω, B, P) → (Ω1, B1)
?? 可測空間 (Ω2, B2)
?? 可測関数 f: Ω1 → Ω2
?? このとき、f(X) は (Ω, B, P) 上の確率変数
?? f(X) の期待値
?? EX[f(X)] とも書く
Remark 1.20 (1)
23
※ 期待値を考えるには
ベクトル空間のような
加算乗算可能となる条件が必要

Remark 1.20 (2) (3)
?? 同じ確率分布に従う2つの確率変数 X と Y
は同じ期待値を持つ
?? E[X] の情報から E[Y] を予測できる
?? 統計的学習理論において、学習誤差から
汎化誤差の期待値を推定することは重要
である
24

Remark 1.20 (4)
?? チェビシェフの不等式 (※マルコフでは?)
?? E[|X|] = C のとき任意の M > 0 に対して
C = E[|X|] ≧ E[|X|]{|X| > M}
≧ M E[1]{|X| > M} = M P(|X| > M)
?? P(|X| > M) ≦ C / M
?? 確率論では同様の導出がよく?われる
25

Remark 1.20 (5) (6)
?? 次が成り?つ
E[|X|] < ∞ ? limM→∞ E[|X|]{|X|≧M} = 0
?? 次を満たす定数 δ > 0 と M0 > 0 が存在
するならば E[|X|] < ∞
?任意の M > M0 に対して
???P(|X| > M) ≦ 1 / M1+δ
26

地図
?? 確率分布 PX
27

定義1.15 確率変数の収束
?? 確率空間 (Ω, B, P) 上の
?? 確率変数の列 {Xn} と確率変数 X
①?概収束 (almost surely, almost everywhere):
P({ω ∈ Ω; limn→∞ Xn(ω) = X(ω)}) = 1
②?p次平均収束(p > 0):
limn→∞ E[(Xn ? X)p] = 0
③?確率収束: 任意の ε に対して
limn→∞ P(D(Xn, X) > ε) = 0
28

Remark 1.21
?? よく知られている確率変数の収束の性質
①? Xn が X に概収束または p次平均収束す
るとき、Xn は X に確率収束する
②? Xn が X に確率収束するとき、Xn は X に
法則収束する (定義は5章)
③? ?般に、概収束は p次平均収束の必要条
件でも?分条件でもない
29

まとめ
?? 確率論の?場から、本書では次で定義さ
れる確率変数の極限定理を与える
ただし X1, X2, …, Xn は確率変数 X と同じ確率
分布に従う独?な確率変数
30

まとめ
?? 中?極限定理: 確率変数の平均と分散
?? 統計的学習理論: ゼータ関数の最?の極
(pole)と特異変動(singular fluctuation)
?? ?偏差理論(large deviation theory)より
Fn / n → pS (S: X のエントロピー)
?? Main Formula Ⅱ(p.34) と Ⅲ(p.38) は、
?偏差理論よりも正確な結果
31

5章へつづく
32出典：野呂俊介『スピーシーズドメイン(5)』

狠狠撸

确率论基础

Recommended

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to 确率论基础 (20)

More from hoxo_m (20)

确率论基础