几何を使った统计のはなし
- 1. 几何を使った统计のはなし ー統計を可視化するー 2012/9/27 #zansa @motivic_
- 2. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 1
- 3. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 2
- 4. 自己紹介(略歴) 大学?院 アメリカの大学で純粋数学(学部:低次元トポロジー、院:代数幾何)を勉強 社会人時代 国の機関で… 再び院へ 興味―生物統計 ―情報幾何 ―代数統計 3
- 5. 自己紹介(略歴) 大学?院 アメリカの大学で純粋数学(学部:低次元トポロジー、院:代数幾何)を勉強 社会人時代 国の機関で… 再び院へ 興味―生物統計 ―情報幾何 ―代数統計 人生ランダムウォーク気味? 4
- 6. モチベーション 統計って計算ばっかり 統計手法を視覚的に見たい! 統計を幾何の世界に持ち込めば、幾何学的な 手法が使える! 5
- 7. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 6
- 9. ?? ____ ━┓ ___ ━┓ / ― \ ┏┛/ ―\ ┏┛ / (●) \ ヽ ? /ノ (●) \ ? / (⌒ (●) / | (●) ⌒) \ /  ̄ヽ__) / | (__ノ ̄ | / ___ / \ / | \ \ _ノ | | / \ 8
- 11. 情報幾何の始まり C.R. Rao 「フィッシャー情報行列をリーマン計量 として考えるのが重要じゃね?」(1945) これの意味の解説から始めます 10
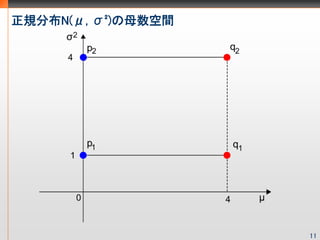
- 12. 正規分布N(μ, σ?)の母数空間 11
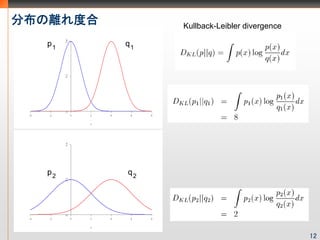
- 13. 分布の离れ度合 Kullback-Leibler divergence p1 q1 p2 q2 12
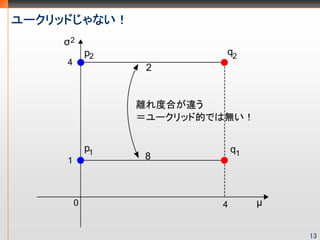
- 14. ユークリッドじゃない! 13
- 15. 碍尝-顿颈惫别谤驳别苍肠别と贵颈蝉丑别谤情报量との関係 対数尤度を として、フィッシャー情報量 を と定義する。 今、 と のKullback-Leibler divergenceにマクロ ーリン展開を使うと、 Iが長さを測るものさしとして使えそう! (参考) 「良い計量」は(定数倍を除き)Iのみであることが証明されています(Cencov) 14
- 16. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 15
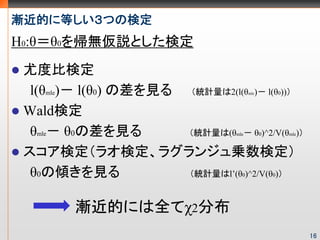
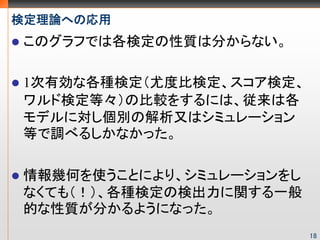
- 17. 漸近的に等しい3つの検定 H0:θ=θ0を帰無仮説とした検定 尤度比検定 l(θmle)- l(θ0) の差を見る (統計量は2(l(θ )- l(θ ))) mle 0 Wald検定 θmle- θ0の差を見る (統計量は(θ - θ )^2/V(θ )) mle 0 mle スコア検定(ラオ検定、ラグランジュ乗数検定) θ0の傾きを見る (統計量はl’(θ )^2/V(θ )) 0 0 漸近的には全てχ2分布 16
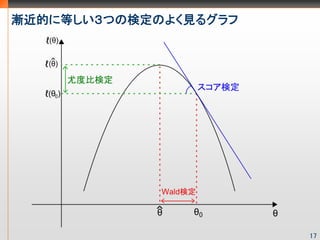
- 18. 渐近的に等しい3つの検定のよく见るグラフ 17
- 20. k-検定 この3つの検定は情報幾何を使うと、1つのクラ スの検定(k-検定)で表現でき、 k=0 の時はWald検定 k=0.5の時は尤度比検定 k=1 の時はスコア検定 と対応付けが出来る。 ※ちなみにkは情報幾何的には検定の受容域の境界面とモデルとの角度の 係数を意味してます。 19
- 21. 定理の前に記号の準備 H0:θ=θ0の検定を考える ,where N is # of samples and I is Fisher Information を検出力関数 を における最強力検定の検出力関数 検出力損出: 最強力検定に対して、同じ検出力を得るにはどれだけ余分に標 本を取らないといけないかを表す。 u(α)を標準正規分布の両側α%点 20
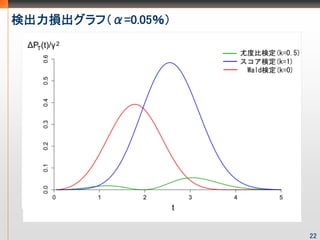
- 22. k-検定の検出力損失の定理 定理 ここで , , はそれぞれ、 はEfron曲率 21
- 23. 検出力损出グラフ(α=0.05%) 22
- 24. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 23
- 25. 最尤法を見る前に 情報幾何を使った最尤法の几何学的解釈の前 に、最小二乗法の古典的な幾何学的解釈を復 習しましょう! 24
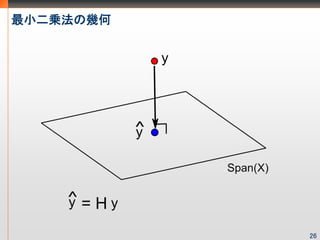
- 26. 最小二乗法の几何 線形回帰モデル としたとき、最小二乗推定量 は =argmin これを解くと、 よって、予測値ベクトル は またハット行列HはH^2=H、HX=Xを満たすことから、yから への対応は、 yからXの列ベクトルが生成するベクトル空間への射影と考えることができる 25
- 27. 最小二乗法の几何 26
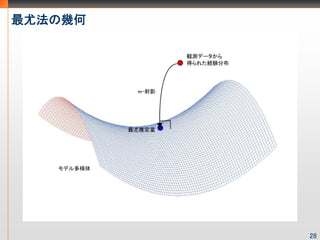
- 28. 最尤法の几何 ここでは空間として指数型分布族を考えます 確率質量関数又は確率密度関数 が次のように書けるとき、 指数型分布族と呼びます: 例)正規分布 27
- 29. 最尤法の几何 28
- 30. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 29
- 31. EMアルゴリズム 尤度が最大となるパラメータを解析的に見つける代わりに、極限 が尤度を最大にするような数列を作るアルゴリズム 最尤推定量が解析的に求めるのが難しい時や、不完全データ の解析に使える eg) 混合正規分布、欠測を含むデータの解析 ここで、 Yを観測されたデータに対応する確率変数 Zを欠測データに対応する確率変数 X=(Y,Z)を完全データに対応する確率変数 とする。 30
- 32. EMアルゴリズム 計算手順 (1) 適当に初期値 を取る (2) 以下のE-ステップとM-ステップを繰り返す E(Expectation)-ステップ: 下記のQを計算する M(Maximization)-ステップ: Qを最大化するθを見つけてθを更新する 31
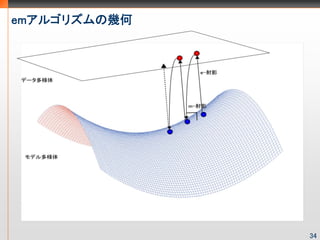
- 33. emアルゴリズムのための言葉の準備 不完全データの場合、空間内の1点ではなく点の集まり である多様体となる。これをデータ多様体と呼ぶ。また 、データ多様体のパラメータをηとし、確率密度関数をq と書く。 e-射影とm-射影は双対的な射影で、それぞれデータ多 様体、モデル多様体への(最短距離での)直交射影と なってます。m-射影は最尤法で出てきたものと同じで、 最尤推定をしていることになります。 32
- 34. emアルゴリズム (1)初期値 をモデル内に適当に取る (2)以下のe-ステップとm-ステップを繰り返す e(exponential)-ステップ 以下のKullback-Leibler divergenceが最小になるηを見つける ( からデータ多様体にe-射影をする) m(mixture)-ステップ 以下のKullback-Leibler divergenceが最小になるθを見つける ( からモデル多様体にm-射影をする) 33
- 35. 别尘アルゴリズムの几何 34
- 36. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 35
- 37. 情報幾何の応用 マルチスケール?ブートストラップ法 ?通常のブートストラップに対し、精度が格段に上 (通常のが1次の精度に対して、3次の精度) ?計算量のオーダーは変わらない ?曲率とかの幾何的な量を計算 ?バイオインフォマティックスの分子系統樹推定で標準 的に使われている 36
- 38. (参考)ブートストラップ法 統計学におけるモンテカルロ法 リサンプリング法の1つ 分布が複雑であったり分からない場合に力を発 揮 サンプルを基に経験分布関数を作り、そこから 乱数を発生させ計算する 37
- 39. 他にも ブートストラップ&マルチスケール?ブートストラ ップも情報幾何を使って「見る」ことができる Jeffreys priorが情報幾何の世界で見ると一様と なる(アメリカの大学だとこのあたりの事実は学 部の低学年向けの統計入門のクラスで教えて いたりします) 38
- 40. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 39
- 42. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 41
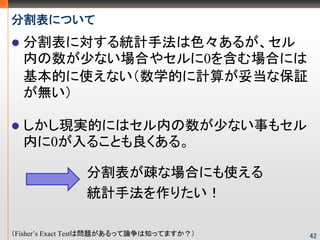
- 43. 分割表について 分割表のセル内の数が少ない場合だと、漸近 理論が使えないため、正確検定の方が良い が、フィッシャーの正確検定は、セル数が多い場 合には(分割表の列挙がNP問題のため)無理 分割表が大きい&疎な場合にも 使える統計手法を作りたい! 42
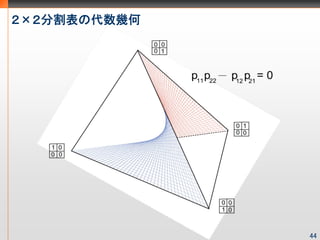
- 44. 2×2分割表の代数几何 Y1 Y2 Total Y1 Y2 Total X1 n11 n12 n1+ X1 p11 p12 p1+ X2 n21 n22 n2+ X2 p21 p22 p2+ Total n+1 n+2 n++ Total p+1 p+2 1 ,を満たすので の集まりは、重心座標を考えると 4面体の内部となる 43
- 45. 2×2分割表の代数几何 44
- 46. Simpson’s paradox 治らな 治った かった 新薬は効いてない? プラセボ 500 500 新薬のオッズ比 OR=0.1 新薬 100 1,000 45
- 47. Simpson’s paradox 治らな 新薬は効いてない? 治った かった プラセボ 500 500 新薬のオッズ比 新薬 100 1,000 OR=0.1 男女で分けると??? 治らな 治らな 男性 治った 女性 治った かった かった プラセボ 5 100 プラセボ 495 400 新薬 80 990 新薬 20 10 OR≒1.6 OR≒1.6 効いてる! 46
- 49. 現実的な応用として グレブナー基底?マルコフ基底を使って分割表を 分析する方法(惭颁惭颁法)があります。 (フィッシャーの方法に比べれば全然良いけど) まだ計算に少し時間がかかるので、現在は計算 の効率を上げるような研究が進んでいます。 48
- 50. 本日の発表内容 自己紹介 情報幾何のはなし 情報幾何って何? 検定への応用 最尤法を「見る」 EMアルゴリズムを「見る」 応用:マルチスケール?ブートストラップ 代数統計のはなし 代数統計って何? 2×2分割表における代数幾何 一般学習モデルへの応用 49
- 51. 代数統計の一般学習モデルへの応用 一般モデルは特異点を持つので、代数幾何を使わない と扱うのが難しい 正則モデル 一般モデル 正規分布 混合正規分布 具体例 線形回帰等 隠れマルコフモデル等 Cramér-Raoの不等式 成立する 成立しない 存在しないか、 最尤推定量 漸近有効性がある 漸近有効性がない WAIC, EoSのみ 情報量基準 AIC, BIC等々 (AIC等は使えない) 50
- 52. WAICのポイント 特異点に対して特異点解消定理を使う。(代数 幾何だからこそできる技) WAICの計算自体は簡単。(代数幾何を使うの は数学的な保証の部分です) 51
- 53. おわり 他にもまだまだ応用があり、今後色々な分野で 活躍をしていく(???ハズ) ! ご清聴ありがとうございました! 52
- 54. 参考文献 S-I.Amari and H.Nagaoka. Methods of information geometry, Translations of mathematical monographs; v. 191, American Mathematical Society, 2000 S-I.Amari. Information geometry of the EM and em algorithms for neural networks. Neural Networks. 8(9) 1379-1408, 1995 P.Gibilisco, et al. Algebraic and Geometric Methods in Statistics, Cambridge University Press, 2009 53