–Т—Ц–і–Ї—А–Є—В–Є–є —Г—А–Њ–Ї
- 4. –Ж–Ж. –Р–Ї—В—Г–∞–ї—Ц–Ј–∞—Ж—Ц—П –Њ–њ–Њ—А–љ–Є—Е –Ј–љ–∞–љ—М. –Ч–∞–Ї—Ц–љ—З–Є—В–Є —А–µ—З–µ–љ–љ—П: 1.–†—Ц–≤–љ—П–љ–љ—П–Љ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П вА¶ 2.–Ъ–Њ—А–µ–љ–µ–Љ —А—Ц–≤–љ—П–љ–љ—П –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—ПвА¶ 3.–†–Њ–Ј–≤вАЩ—П–Ј–∞—В–Є —А—Ц–≤–љ—П–љ–љ—П –Њ–Ј–љ–∞—З–∞—Ф вА¶ 4. –Ф–≤–∞ —А—Ц–≤–љ—П–љ–љ—П –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П —А—Ц–≤–љ–Њ—Б–Є–ї—М–љ–Є–Љ–Є, —П–Ї—Й–ЊвА¶ 5. –Ч–∞–≤–ґ–і–Є –њ—А–∞–≤–Є–ї—М–љ—Ц —В–∞–Ї—Ц –Њ—Б–љ–Њ–≤–љ—Ц –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц —А—Ц–≤–љ—П–љ—МвА¶
- 5. –Т–Є–Ї–Њ–љ–∞–љ–љ—П —Г—Б–љ–Є—Е –≤–њ—А–∞–≤. –Я–µ—А–µ—В–≤–Њ—А–Є—В–Є —Г –Љ–љ–Њ–≥–Њ—З–ї–µ–љ –≤–Є—А–∞–Ј: (—Е-2)(2+—Е); (—Е-3)2; (—Г¬≥-—Г)¬Ј—Г; (—Г-1)(—Г+2). –І–Є —А—Ц–≤–љ–Њ—Б–Є–ї—М–љ—Ц —А—Ц–≤–љ—П–љ–љ—П: 3—Е-2=—Е+3 —Ц 2—Е-5=0; 5—Е-1=3—Е-—Е¬≤ —Ц —Е¬≤+2—Е-1=0; 0,5—Е-3=0 —Ц —Е-6=0; 5—Е¬≤-10—Е+25=0 —Ц —Е¬≤-2—Е+5=0? –Т—Ц–і–њ–Њ–≤—Ц–і—М –Њ–±–≥—А—Г–љ—В—Г–≤–∞—В–Є.
- 7. –Ж–Ж–Ж. –Т—Б—В—Г–њ–љ–µ —Б–ї–Њ–≤–Њ –Ж—Б—В–Њ—А—Ц—П –≤–Є–љ–Є–Ї–љ–µ–љ–љ—П –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ —А—Ц–≤–љ—П–љ–љ—П
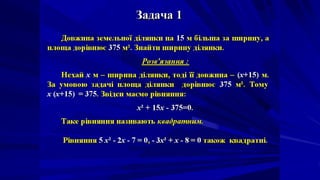
- 8. –Ж—Б—В–Њ—А–Є—З–љ–∞ –і–Њ–≤—Ц–і–Ї–∞ –Ъ–≤–∞–і—А–∞—В–љ—Ц —А—Ц–≤–љ—П–љ–љ—П –≤ –°—В–∞—А–Њ–і–∞–≤–љ—М–Њ–Љ—Г –Т–∞–≤—Ц–ї–Њ–љ—Ц –Э–µ–Њ–±—Е—Ц–і–љ—Ц—Б—В—М —А–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞—В–Є —А—Ц–≤–љ—П–љ–љ—П –љ–µ —В—Ц–ї—М–Ї–Є –њ–µ—А—И–Њ–≥–Њ —Б—В–µ–њ–µ–љ—П, –∞ –є –і—А—Г–≥–Њ–≥–Њ —Й–µ –≤ –і–∞–≤–љ–Є–љ—Г –±—Г–ї–∞ –≤–Є–Ї–ї–Є–Ї–∞–љ–∞ –љ–µ–Њ–±—Е—Ц–і–љ—Ц—Б—В—О —А–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞—В–Є –Ј–∞–і–∞—З—Ц, –њ–Њ–≤вАЩ—П–Ј–∞–љ—Ц —Ц–Ј –Ј–љ–∞—Е–Њ–і–ґ–µ–љ–љ—П–Љ –њ–ї–Њ—Й –Ј–µ–Љ–µ–ї—М–љ–Є—Е –і—Ц–ї—П–љ–Њ–Ї —Ц –Ј –Ј–µ–Љ–µ–ї—М–љ–Є–Љ–Є —А–Њ–±–Њ—В–∞–Љ–Є –≤–Њ—Ф–љ–љ–Њ–≥–Њ —Е–∞—А–∞–Ї—В–µ—А—Г, –∞ —В–∞–Ї–Њ–ґ –Ј —А–Њ–Ј–≤–Є—В–Ї–Њ–Љ –∞—Б—В—А–Њ–љ–Њ–Љ—Ц—Ч —Ц —Б–∞–Љ–Њ—Ч –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є. –Ъ–≤–∞–і—А–∞—В–љ—Ц —А—Ц–≤–љ—П–љ–љ—П –≤–Љ—Ц–ї–Є —А–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞—В–Є –ґ–Є—В–µ–ї—Ц –Т–∞–≤—Ц–ї–Њ–љ—Г 2000 —А–Њ–Ї—Ц–≤ –і–Њ –љ–∞—И–Њ—Ч –µ—А–Є. –Т–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—З–Є —Б—Г—З–∞—Б–љ–Є–є –∞–ї–≥–µ–±—А–∞—Ч—З–љ–Є–є –Ј–∞–њ–Є—Б, –Љ–Њ–ґ–љ–∞ —Б–Ї–∞–Ј–∞—В–Є, —Й–Њ –≤ –Ї–ї–Є–љ–Њ–њ–Є—Б–љ–Є—Е —В–µ–Ї—Б—В–∞—Е –Ј—Г—Б—В—А—Ц—З–∞—О—В—М—Б—П –Ї—А—Ц–Љ –љ–µ–њ–Њ–≤–љ–Є—Е, —В–∞–Ї–Њ–ґ —Ц –њ–Њ–≤–љ—Ц –Ї–≤–∞–і—А–∞—В–љ—Ц —А—Ц–≤–љ—П–љ–љ—П.
- 9. –Я—А–∞–≤–Є–ї–Њ —А–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞–љ–љ—П —Ж–Є—Е —А—Ц–≤–љ—П–љ—М, –≤–Є–Ї–ї–∞–і–µ–љ–µ –≤ —В–µ–Ї—Б—В–∞—Е –Т–∞–≤—Ц–ї–Њ–љ—Г, —Б–њ—Ц–≤–њ–∞–і–∞—Ф –Ј —Б—Г—З–∞—Б–љ–Є–Љ, –∞–ї–µ –љ–µ–≤—Ц–і–Њ–Љ–Њ —П–Ї–Є–Љ —З–Є–љ–Њ–Љ –ґ–Є—В–µ–ї—Ц –Т–∞–≤—Ц–ї–Њ–љ—Г –њ—А–Є–є—И–ї–Є –і–Њ —Ж—М–Њ–≥–Њ –њ—А–∞–≤–Є–ї–∞. –Ь–∞–є–ґ–µ –≤—Б—Ц –Ј–љ–∞–є–і–µ–љ—Ц –і–Њ —Ж—М–Њ–≥–Њ —З–∞—Б—Г –Ї–ї–Є–љ–Њ- –њ–Є—Б–љ—Ц —В–µ–Ї—Б—В–Є –≤–Є–Ї–ї–∞–і–µ–љ—Ц —Г –≤–Є–≥–ї—П–і—Ц —А–µ—Ж–µ–њ—В—Ц–≤ —А–Њ–Ј–≤вАЩ—П–Ј–∞–љ—Ц –Ј–∞–і–∞—З—Ц, —Ц –љ—Ц–і–µ –љ–µ –≤–Ї–∞–Ј–∞–љ–Њ —П–Ї –≤–Њ–љ–Є –і–Њ —Ж—М–Њ–≥–Њ –њ—А–Є–є—И–ї–Є. –Э–µ–Ј–≤–∞–ґ–∞—О—З–Є –љ–∞ –≤–Є—Б–Њ–Ї–Є–є —А—Ц–≤–µ–љ—М —А–Њ–Ј–≤–Є—В–Ї—Г –∞–ї–≥–µ–±—А–Є —Г –Т–∞–≤—Ц–ї–Њ–љ—Ц, –≤ –Ї–ї–Є–љ–Њ–њ–Є—Б–љ–Є—Е —В–µ–Ї—Б—В–∞—Е –≤—Ц–і—Б—Г—В–љ—Ф –њ–Њ–љ—П—В—В—П –≤—Ц–івАЩ—Ф–Љ–љ–Њ–≥–Њ —З–Є—Б–ї–∞ —Ц –Ј–∞–≥–∞–ї—М–љ—Ц –Љ–µ—В–Њ–і–Є —А–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞–љ–љ—П –Ї–≤–∞–і—А–∞—В–љ–Є—Е —А—Ц–≤–љ—П–љ—М.
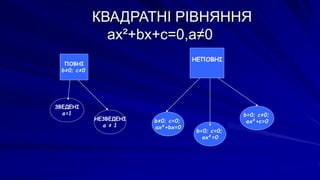
- 15. –І–Є—Б–ї–∞ a, b, c вАУ –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–Є –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ —А—Ц–≤–љ—П–љ–љ—П a вАУ –њ–µ—А—И–Є–є –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В, b вАУ –і—А—Г–≥–Є–є –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В, c вАУ –≤—Ц–ї—М–љ–Є–є —З–ї–µ–љ. –†—Ц–≤–љ—П–љ–љ—П –≤–Є–і—Г ax¬≤+bx+c=0, –і–µ —Е вАУ –Ј–Љ—Ц–љ–љ–∞; a, b, c вАУ –і–∞–љ—Ц —З–Є—Б–ї–∞, –њ—А–Є—З–Њ–Љ—Г –∞вЙ†0, –љ–∞–Ј–Є–≤–∞—О—В—М –Ї–≤–∞–і—А–∞—В–љ–Є–Љ.
- 18. –Ъ–Т–Р–Ф–†–Р–Ґ–Э–Ж –†–Ж–Т–Э–ѓ–Э–Э–ѓ ax¬≤+bx+c=0,aвЙ†0 –Я–Ю–Т–Э–Ж bвЙ†0; cвЙ†0 –Э–Х–Я–Ю–Т–Э–Ж –Ч–Т–Х–Ф–Х–Э–Ж a=1 –Э–Х–Ч–Т–Х–Ф–Х–Э–Ж a вЙ† 1 bвЙ†0; c=0; –∞—Е¬≤+b—Е=0 b=0; c=0; –∞—Е¬≤=0 b=0; cвЙ†0; –∞—Е¬≤+—Б=0
- 19. –Э–∞–њ—А–Є–Ї–ї–∞–і 5—Е¬≤=0; 3—Е¬≤-12—Е=0; 25—Е¬≤-4=0; —Е=0. 3—Е(—Е-4)=0; 25—Е¬≤=4; 3—Е=0; —Е-4=0; —Е¬≤=4/25; —Е1=0; —Е2=4. —Е1=2/5; —Е2=-2/5.
- 20. V. –§–Њ—А–Љ—Г–≤–∞–љ–љ—П –≤–Љ—Ц–љ—М —А–Њ–Ј–≤вАЩ—П–Ј—Г–≤–∞—В–Є –≤–њ—А–∞–≤–Є
- 21. 1. –†–Њ–±–Њ—В–∞ –Ј –Ї–∞—А—В–Њ—З–Ї–∞–Љ–Є. –Я–Њ–Ї–∞–ґ—Ц—В—М –Ј–∞ –і–Њ–њ–Њ–Љ–Њ–≥–Њ—О —Б—В—А—Ц–ї–Њ—З–Њ–Ї –Ј–≤вАЩ—П–Ј–Њ–Ї –Љ—Ц–ґ –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–∞–Љ–Є –љ–µ–њ–Њ–≤–љ–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ —А—Ц–≤–љ—П–љ–љ—П.
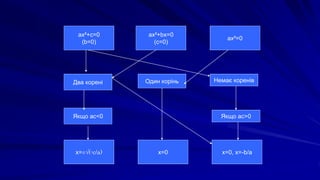
- 22. ax¬≤+c=0 (b=0) ax¬≤+bx=0 (c=0) ax¬≤=0 x=0, x=-b/ax=0x=¬±вИЪ(-c/a) –Ф–≤–∞ –Ї–Њ—А–µ–љ—Ц –Ю–і–Є–љ –Ї–Њ—А—Ц–љ—М –Э–µ–Љ–∞—Ф –Ї–Њ—А–µ–љ—Ц–≤ –ѓ–Ї—Й–Њ –∞—Б<0 –ѓ–Ї—Й–Њ –∞—Б>0
- 23. ax¬≤+c=0 (b=0) ax¬≤+bx=0 (c=0) ax¬≤=0 x=0, x=-b/ax=0x=¬±вИЪ(-c/a) –Ф–≤–∞ –Ї–Њ—А–µ–љ—Ц –Ю–і–Є–љ –Ї–Њ—А—Ц–љ—М –Э–µ–Љ–∞—Ф –Ї–Њ—А–µ–љ—Ц–≤ –ѓ–Ї—Й–Њ –∞—Б<0 –ѓ–Ї—Й–Њ –∞—Б>0
- 24. –†–Њ–±–Њ—В–∞ –Ј –њ—Ц–і—А—Г—З–љ–Є–Ї–Њ–Љ: вДЦ861, 862, 863, 866.
- 25. 2. –Я–Є—Б—М–Љ–Њ–≤—Ц –≤–њ—А–∞–≤–Є –Ч–љ–∞–є—В–Є –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–Є –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ —А—Ц–≤–љ—П–љ–љ—П: –∞) 5—Е¬≤-9—Е+4=0, –±) —Е¬≤+3—Е-10=0, –≤) -x¬≤-8—Е+1=0, –≥) -4—Е¬≤+5—Е=0, –і) 6—Е¬≤-30=0, –µ) 9—Е¬≤=0
- 27. –Ч–∞–њ–Є—Б–∞—В–Є –Ї–≤–∞–і—А–∞—В–љ–µ —А—Ц–≤–љ—П–љ–љ—П —Ц–Ј –Ј–∞–і–∞–љ–Є–Љ–Є –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–∞–Љ–Є: –∞) –∞=5, b=-9, —Б=4; –±) –∞=1, b=2, —Б=-9; –≤) –∞=-1, b=-5, —Б=1; –≥) –∞=-2, b=6, —Б=0; –і) –∞=7, b=0, —Б=-37; –µ) –∞=10, b=0, —Б=0
- 29. вДЦ 870, 871, 872, 874, 875, 878 вАУ –Ї–Њ–ї–µ–Ї—В–Є–≤–љ–µ —А–Њ–Ј–≤'—П–Ј—Г–≤–∞–љ–љ—П.
- 30. VI. –Ф–Њ–Љ–∞—И–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П. –Т–Є–≤—З–Є—В–Є —В–µ–Њ—А–µ—В–Є—З–љ–Є–є –Љ–∞—В–µ—А—Ц–∞–ї, –њ–∞—А–∞–≥—А–∞—Д 19. –Я–Є—Б—М–Љ–Њ–≤–Њ вДЦ869, 873, 876, 879. –Я–Њ–≤—В–Њ—А–Є—В–Є –≤–њ—А–∞–≤–Є –љ–∞ –≤–Є–і—Ц–ї–µ–љ–љ—П –њ–Њ–≤–љ–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–∞ –і–≤–Њ—З–ї–µ–љ–∞.
- 31. VII. –Я—Ц–і—Б—Г–Љ–Ї–Є —Г—А–Њ–Ї—Г. –Т–Є–Ї–Њ–љ–∞–љ–љ—П —В–µ—Б—В—Ц–≤. –ѓ–Ї–µ —Ц–Ј –і–∞–љ–Є—Е —А—Ц–≤–љ—П–љ—М —Ф –Ї–≤–∞–і—А–∞—В–љ–Є–Љ? 1.–∞) 3—Е¬≤-5—Е=—Е-3; –±) 7x+11=0; –≤) x(x-l)=x¬≤-2x; –≥)(—Е-7):—Е=0. 2.–∞) 3x=2; –±) 7x¬≤=9x+12; –≤) x(x+3)=x¬≤-2x; –≥) (—Е+1):—Е=0. 3.–∞)2—Е+1=0; –±)—Е(—Е+3)=—Е2-9—Е; –≤) 5xz+3x=x+7; –≥)(—Е+4):—Е=0 4. –∞)4x¬≤-9x+3=0; –±) 7x+14=0; –≤)—Е(—Е+3)=—Е¬≤-7—Е+5; –≥)(—Е-2):—Е=5.
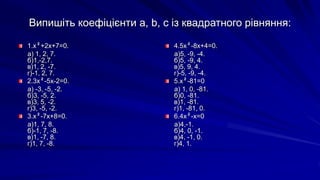
- 32. –Т–Є–њ–Є—И—Ц—В—М –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–Є –∞, b, —Б —Ц–Ј –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ —А—Ц–≤–љ—П–љ–љ—П: 1.x¬≤+2x+7=0. –∞) 1, 2, 7. –±)1,-2,7. –≤)1, 2, -7. –≥)-1, 2, 7. 2.3x¬≤-5x-2=0. –∞) -3, -5, -2. –±)3, -5, 2. –≤)3, 5, -2. –≥)3, -5, -2. 3.x¬≤-7x+8=0. –∞)1, 7, 8. –±)-1, 7, -8. –≤)1, -7, 8. –≥)1, 7, -8. 4.5x¬≤-8x+4=0. –∞)5, -9, -4. –±)5, -9, 4. –≤)5, 9, 4. –≥)-5, -9, -4. 5.x¬≤-81=0 –∞) 1, 0, -81. –±)0, -81. –≤)1, -81. –≥)1, -81, 0. 6.4—Е¬≤-—Е=0 –∞)4,-1. –±)4, 0, -1. –≤)4, -1, 0. –≥)4, 1.