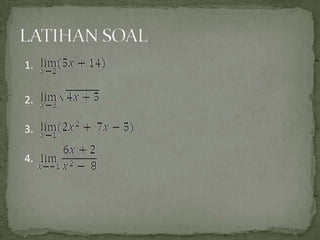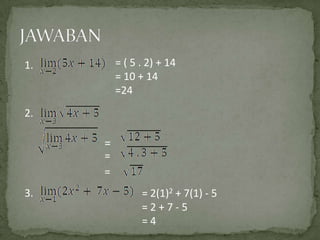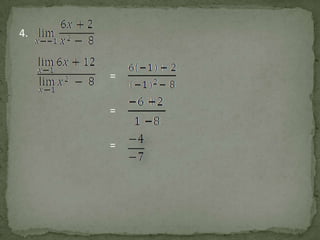Teorema limit
Download as pptx, pdf13 likes48,904 views
Dokumen ini membahas teorema limit dalam menghitung limit fungsi dengan menyederhanakan rumus-rumus yang kompleks. Terdapat delapan sifat limit yang dijelaskan dengan contoh-contoh yang konkret. Tujuan dari dokumen ini adalah memberikan pemahaman yang lebih jelas mengenai cara menghitung limit di suatu titik.
Teorema limit
- 2. Nama Kelompok : 1. Putri Widya Arsani Silvia (31) 2.Riska Prasetyo Utami (32) 3.Saniska Widayanti (33) 4.Sugi Almantara (34) 5.Sukrianingsih (35) 6.Teresa Giovana (36)
- 4. Menghitung limit fungsi di suatu titik dengan menggunakan definisi dan pembuktian seperti yang telah diuraikan sebelumnya adalah pekerjaan rumit. Semakin rumit bentuk fungsinya, semakin rumit pula masalah yang dihadapi. Untuk itu berikut ini diberikan suatu rangkaian rumus-rumus menghitung limit di suatu titik dengan cara sederhana.
- 5. Sifat Pertama 1. Jika limit sebuah konstanta, untuk x mendekati a maka hasilnya adalah konstanta itu sendiri. Contoh Pertama: 1. Jadi Contoh Kedua: 2. Jadi
- 6. Sifat Kedua 2. Jika limit sebuah variabel, untuk x mendekati a maka hasilnya mendekati a. Contoh : 1. 2. Jadi Jadi
- 7. Sifat Ketiga 3. Jika limit sebuah konstanta dikali sebuah fungsi f(x) untuk x mendekati a, maka sama dengan sebuah konstanta dikali limit sebuah fungsi f(x) untuk x mendekati a. Contoh : a. Jawab 5 = 5.(2.2+2) = 5(4+2) = 5(6) = 30
- 8. b. Jawab = 4 (2) =8 Jadi hasilnya mendekati 8
- 9. Sifat Keempat 4. Jika limit sebuah fungsi f(x) ditambah fungsi g(x) , untuk x mendekati a, maka sama dengan limit fungsi f(x) untuk x mendekati a ditambah limit fungsi g(x) untuk x mendekati a. Contoh: Dit: f(x) = x+2 g(x) = 2x-1
- 10. Jawab = (1+2) + ( 2 . 1 1) Jadi hasil = 3+1 =4
- 11. Sifat Kelima 5. Jika limit sebuah fungsi f(x) dikurang fungsi g(x), untuk x mendekati a, maka sama dengan limit fungsi f(x) untuk x mendekati a dikurang limit fungsi g(x) untuk x mendekati a . Contoh : 5) f(x) = x +2 , g(x) = 2x-1
- 12. Jawab : = ( 1 + 2 ) ( 2.1 1 ) =31 =2
- 13. Sifat Keenam 6. Jika limit sebuah fungsi f(x) dibagi dengan fungsi g(x) untuk x mendekati a sama dengan limit sebuah fungsi f(x) untuk x mendekati a dibagi limit sebuah fungsi g(x) untuk x mendekati a. Contoh f(x) = -1 g(x) = -1
- 14. = = =
- 15. 甼 Sifat Ketujuh 7. Jika limit , untuk x mendekati a, sama dengan Contoh : = 7 (3)族 = 7 (9) = 63
- 16. Sifat Kedelapan 8. untuk x mendekati a sama dengan Contoh = = =
- 17. 1. 2. 3. 4.
- 18. = ( 5 . 2) + 14 = 10 + 14 =24 1. 2. = = = 3. = 2(1)2 + 7(1) - 5 =2+7-5 =4
- 19. 4. = = =