limit fungsi
- 1. ’éĘ x = a film Kawat 1 ’éĘ ’éĘ x = a film ’éĘ y= f(x) L1 X X BAB 7 Limit Fungsi
- 2. Standar Kompetensi: ’ü▒ Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah Kompetensi Dasar: ’ü▒ Menggunakan secara intuitif arti limit fungsi di suatu titik dan di takhingga. ’ü▒ Menggunakan sifat limit fungsi untuk menghitung bentuk tak tentu fungsi aljabar dan trigonometri.
- 3. PENGERTIAN LIMIT FUNGSI Melalui Pengamatan Grafik Fungsi Pengertian limit fungsi di sebuah titik melalui pengamatan grafik fungsi di sekitar titik itu, dapat dideskripsikan dengan menggunakan alat peraga dua buah potongan kawat dan satu lembaran film tipis. ’éĘ x = a film Kawat 1 ’éĘ ’éĘ x = a film ’éĘ y= f(x) L1 X X
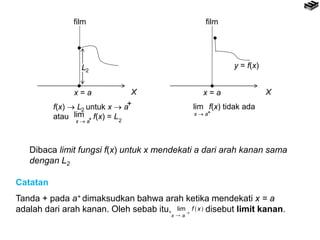
- 4. Dibaca limit fungsi f(x) untuk x mendekati a dari arah kiri sama dengan L1 Catatan Tanda ’ĆŁ pada a- dimaksudkan bahwa arah ketika mendekati x = a adalah dari arah kiri. Oleh sebab itu, disebut limit kiri. Dalam matematika, perkiraan ketinggian titik ujung kawat terhadap sumbu X dikatakan sebagai limit fungsi f(x) untuk x mendekati dari arah kiri. Misalkan ketinggian yang diperkirakan itu adalah L1 maka notasi singkat untuk menuliskan pernyataan itu adalah
- 5. ’éĘ ’éĘ ’éĘ ’éĘ y = f(x) x = a x = a L2 film film f(x) ’é« L untuk x ’é« a atau f(x) = L + lim x ’é« a+ 2 2 lim x ’é« a+ f(x) tidak ada X X Catatan Tanda + pada a+ dimaksudkan bahwa arah ketika mendekati x = a adalah dari arah kanan. Oleh sebab itu, disebut limit kanan. Dibaca limit fungsi f(x) untuk x mendekati a dari arah kanan sama dengan L2
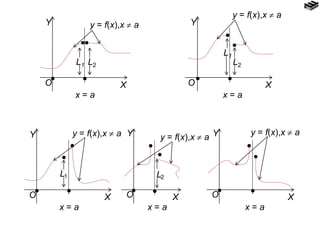
- 6. ’éĘ ’éĘ ’éĘ ’éĘ X Y x = a y = f(x),x ’é╣ a L2 L1 O ’éĘ ’éĘ ’éĘ’éĘ X Y x = a L2L1 y = f(x),x ’é╣ a O ’éĘ ’éĘ ’éĘ ’éĘ X Y x = a y = f(x),x ’é╣ a O L1 ’éĘ L2 ’éĘ ’éĘ y = f(x),x ’é╣ a ’éĘ ’éĘ ’éĘ x = a x = a X X Y Y ’éĘ O ’éĘ O y = f(x),x ’é╣ a
- 7. No. Limit Kiri Limit Kanan 1. 2. 3. 4. 5. ada, nilainya L1 ada, nilainya L1 ada, nilainya L1 tidak ada tidak ada ada, nilainya L2 ada, nilainya L2 tidak ada ada, nilainya L2 tidak ada L1 = L2 = L L1 ’é╣ L2 ada, nilainya L tidak ada tidak ada tidak ada tidak ada lim f(x) x ’é« a+ lim f(x) x ’é« a’ĆŁ lim f(x) x ’é« a
- 8. Suatu fungsi y = f(x) didefinisikan untuk x di sekitar a, maka lim f(x) = L jika dan hanya jika lim (x) = lim f(x) = L. Definisi: x ’āĀ a+ x ’āĀ a- x ’āĀ a
- 9. Pengertian Limit Fungsi melalui Perhitungan Nilai-Nilai Fungsi x 1,7 1,8 1,99 1,999 ’é«2,000’é¼ 2,001 2,01 2,1 2,2 3,8 3,8 3,99 3,999 . . ? . . . 4,001 4,01 4,1 4,2 Contoh Diketahui fungsi f(x) = dengan daerah asal Df = {x l x ’āÄ R dan x ’é╣ 2}. Hitunglah nilai lim f(x) dengan cara menghitung nilai-nilai fungsi di sekitar x = 2. x2 ’ĆŁ 4 x ’ĆŁ 2 x ’āĀ 2 Jawab: Nilai-nilai fungsi f(x) = di sekitar x = 2x2 ’ĆŁ 4 x ’ĆŁ 2 x2 ’ĆŁ 4 x ’ĆŁ 2 Berdasarkan Tabel di atas, terlihat bahwa f(x) = mendekati nilai L = 4 ketika x mendekati 2 baik dari kiri maupun kanan. x2 ’ĆŁ 4 x ’ĆŁ 2 Dengan demikian, lim f(x) = lim = 4 x2 ’ĆŁ 4 x ’ĆŁ 2x ’āĀ 2 x ’āĀ 2
- 10. Beberapa hal yang perlu diperhatikan tentang f(x) = x2 ’ĆŁ 4 x ’ĆŁ 2 f(2) = x2 ’ĆŁ 4 x ’ĆŁ 2 = 0 0 Bentuk disebut sebagai bentuk tak tentu dan tidak didefinisikan.0 0 0 0 Untuk x ’é╣ 2, fungsi f(x) = dapat disederhanakan menjadi x2 ’ĆŁ 4 x ’ĆŁ 2 f(x) = = x + 2 (x + 4) (x ’ĆŁ 2) x ’ĆŁ 2 Grafik fungsi Y X1 2 3 4 5 1 2 3 4 5 ’ĆŁ2’ĆŁ1 o ’éĘ ’éĘ ’éĘ ┬║y = f(x) = x2 ’ĆŁ 4 x ’ĆŁ 2 , x ’é╣ 2 y = f(x) = x2 ’ĆŁ 4 x ’ĆŁ 2 untuk x ’é╣ 2 adalah sebuah garis lurus dengan persamaan yang terputus di titik (2, 4)y = f(x) = x + 2
- 11. LIMIT FUNGSI ALJABAR Menentukan Limit Fungsi Aljabar yang Berbentuk lim f(x) x ’é« a Metode Substitusi Langsung Contoh lim (x2 ’ĆŁ 2x + 1) = (’ĆŁ1)2 ’ĆŁ 2(’ĆŁ1) + 1 = 4 x ’é« ’ĆŁ1 Jadi, lim (x2 ’ĆŁ 2x + 1) = 4 x ’é« ’ĆŁ1
- 12. Metode Pemfaktoran lim x ’é« 2 x2 ’ĆŁ 4 x ’ĆŁ 2 = 22 ’ĆŁ 4 2 ’ĆŁ 2 = 0 0 0 0 disebut bentuk tak tentu dan tidak didefinisikan. Oleh karena itu, diperlukan upaya lain. Salah satunya dengan cara mencari faktor persekutuan yang sama antara bagian pembilang dan bagian penyebut . lim x ’é« 2 x2 ’ĆŁ 4 x ’ĆŁ 2 = lim x ’é« 2 (x ’ĆŁ 2) (x + 2) x ’ĆŁ 2 , sebab x ’é╣ 2 atau x ’ĆŁ 2 ’é╣ 0 = lim x ’é« 2 (x + 2) = 4
- 13. Secara umum, pengerjaan limit fungsi yang mempunyai bentuk tak tentu dapat dilakukan dengan menggunakan metode pemfaktoran. f(x) g(x) = f(a) g(a) = 0 0x ’é« a Misalkan lim . Upayakan f(x) dan g(x) memilki faktor yang sama dan faktor yang sama itu adalah (x ’ĆŁ a), sehingga: p(x) q(x) = p(a) q(a) lim x ’é« a f(x) g(x) = lim x ’é« a (x ’ĆŁ a) ’āŚ p(x) (x ’ĆŁ a) ’āŚ q(x) = lim x ’é« a , dengan syarat p(a) ’é╣ 0 dan q(a) ’é╣ 0. x ’ĆŁ a = 1 x ’ĆŁ a Perhatikan bahwa , sebab nilai x hanya dekat dengan a sehingga x - a ’é╣ 0.
- 14. lim x ’é« 3 x2 ’ĆŁ 9 x2 + 7 ’ĆŁ 4 = lim x ’é« 3 x2 ’ĆŁ 9 x2 + 7 ’ĆŁ 4 ’é┤ x2 + 7 + 4 x2 + 7 + 4 = lim x ’é« 3 (x2 ’ĆŁ 9)( x2 + 7 + 4) (x2 + 7) ’ĆŁ 16 = lim x ’é« 3 ( x2 + 7 + 4) = (32 + 7) + 4 = 8 = lim x ’é« 3 (x2 ’ĆŁ 9)( x2 + 7 + 4) (x2 ’ĆŁ 9) Contoh
- 15. Menentukan Limit Fungsi Aljabar yang Berbentuk lim f(x) x ’é« ’éź Pengertian Tak Hingga Y X ’éĘ x = a ’éĘ O Y X ’éĘ x = a ’éĘ O Y X ’éĘ x = a ’éĘ O y = f(x) y = f(x) y = f(x) lim f(x) = ’éź x ’é« a’ĆŁ lim f(x) = ’éź x ’é« a+ lim f(x) = ’éź x ’é« a Y X ’éĘ ’éĘ x = aO y = f(x) Y X ’éĘ ’éĘ x = aO y = f(x) Y X ’éĘ ’éĘ x = aO y = f(x) lim f(x) = ’ĆŁ’éź x ’é« a’ĆŁ lim f(x) = ’ĆŁ’éź x ’é« a+ lim f(x) = ’ĆŁ’éź x ’é« a
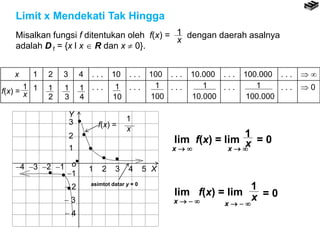
- 16. Limit x Mendekati Tak Hingga Misalkan fungsi f ditentukan oleh f(x) = dengan daerah asalnya adalah D f = {x l x ’āÄ R dan x ’é╣ 0}. 1 x x 1 2 3 4 . . . 10 . . . 100 . . . 10.000 . . . 100.000 . . . ’ā× ’éź . . . . . . . . . . . . . . . ’ā× 0 Y X1 2 3 4 5 3 ’ĆŁ1 ’ĆŁ1 o ’éĘ ’éĘ ’éĘ 2 1 ’ĆŁ 2 ’ĆŁ 3 ’ĆŁ 4 ’ĆŁ2’ĆŁ3’ĆŁ4 ’éĘ ’éĘ ’éĘ ’éĘ ’éĘ ’éĘ f(x) = 1 x asimtot datar y = 0 lim f(x) = lim x ’é« ’éź x ’é« ’éź 1 x = 0 lim f(x) = lim x ’é« ’ĆŁ ’éź x ’é« ’ĆŁ ’éź 1 x = 0 f(x) = 1 x 1 2 1 3 1 4 1 10 1 100 1 10.000 1 100.000 1
- 17. Menentukan Limit Fungsi Aljabar Jika x ’é« ’éź 1. Membagi dengan Pangkat Tertinggi dari Penyebut 1. Jika derajat f(x) = derajat g(x) maka lim x ’é« ’éź f(x) g(x) = koefesien pangkat tertinggi dari f(x) koefesien pangkat tertinggi dari g(x) 2. (i) Jika derajat f(x) ’ĆŠ derajat g(x) dan koefisien pangkat tertinggi f(x) bernilai positif, maka (ii) Jika derajat f(x) ’ĆŠ derajat g(x) dan koefisien pangkat tertinggi f(x) bernilai negatif, maka lim x ’é« ’éź f(x) g(x) = ’éź lim x ’é« ’éź f(x) g(x) = ’ĆŁ ’éź 3. Jika derajat f(x) < derajat g(x) maka lim x ’é« ’éź f(x) g(x) = 0 f(x) g(x)x ’é« ’éź Berdasarkan derajat dan koefesien pangkat tertinggi, lim dapat ditetapkan sebagai berikut.
- 18. 2. Mengalikan dengan Faktor Lawan Contoh lim x ’é« ’éź 2x ’ĆŁ 1’ĆŁ 3x + 5{ } = = = lim x ’é« ’éź 2x ’ĆŁ 1’ĆŁ 3x + 5{ }’é┤ 2x ’ĆŁ 1+ 3x + 5 2x ’ĆŁ 1+ 3x + 5 lim x ’é« ’éź (2x ’ĆŁ 1) (3x + 5) 2x ’ĆŁ 1+ 3x + 5 ’ĆŁ lim x ’é« ’éź ’ĆŁ x ’ĆŁ 6 2x ’ĆŁ 1+ 3x + 5 = ’ĆŁ ’éź (perhatikan ketentuan butir 2 bagian (ii)) f(x) g(x){ ’ĆŁ } f(x) g(x)+ f(x) g(x)+ x ’é« ’éź Limit fungsi yang berbentuk lim dapat diselesaikan dengan cara mengalikan dengan faktor lawan, yaitu .
- 19. TEOREMA LIMIT 1. Jika f(x) = k maka lim f(x) = k (untuk setiap k konstan dan a bilangan real). x ’é« a 2. Jika f(x) = x maka lim f(x) = a (untuk setiap a bilangan real). x ’é« a 3. a) lim {f(x) + g(x)} = lim f(x) + lim g(x) b) lim {f(x) ’ĆŁ g(x)} = lim f(x) ’ĆŁ lim g(x) x ’é« a x ’é« ax ’é« a x ’é« a 4. Jika k suatu konstanta maka lim k ’āŚ f(x) = k lim f(x). x ’é« a x ’é« a x ’é« a x ’é« a x ’é« a 5. a) lim {f(x) ’āŚ g(x)} = lim f(x) ’āŚ lim g(x) b) lim f(x) g(x) = lim f(x) x ’é« a x ’é« a lim g(x) x ’é« a , dengan lim g(x) ’é╣ 0x ’é« a lim f(x) x ’é« a n f(x) n = , dengan lim f(x) ’é│ 0 untuk n genap. x ’é« a 6. a) lim {f(x)}n b) lim x ’é« a x ’é« a lim f(x) x ’é« a { } n .= Sifat-sifat limit fungsi dapat dirangkum dalam Teorema Limit sebagai berikut.
- 20. LIMIT FUNGSI TRIGONOMETRI Rumus-Rumus Limit Fungsi Trigonometri lim x ’é« 0 lim x ’é« 0 x sin x sin x x = = 1 lim x ’é« 0 lim x ’é« 0 x tan x tan x x = = 1 lim u ’é« 0 lim x ’é« 0 u sin u sin u u = = 1 lim u’é« 0 lim x ’é« 0 u tan u tan u u = = 1 Contoh Hitunglah lim x ’é« 0 sin 6x 2x Jawab: Misalkan 6x = u, maka x = u. 1 6 Jika x ’é«0 maka u ’é«0, sehingga: lim x ’é« 0 sin 6x 2x = lim u ’é« 0 sin u 2( ) u1 6 lim u ’é« 0 sin u u = lim u ’é« 0 sin u u =3 3 3 (1) = 3 Jadi, lim x ’é« 0 sin 6x 2x = 3