![Dua Masalah Fundamental Kalkulus
• Masalah 1 (Masalah Tangen):
Diberikan sebuah titik P(x,f(x)) pada kurva y=f(x),
bagaimana menentukan kemiringan garis tangen
pada P?
• Masalah 2 (Masalah Luas):
Jika f(x)≥ 0 untuk x∈[a,b], bagaimana menghitung
luas daerah A yaitu suatu bidang yang berada
diantara kurva y=f(x) dan sumbu-x sepanjang
selang [a,b]?](https://image.slidesharecdn.com/bab2-161021045042/85/materi-limit-kuliah-mahasiswa-limit-2-320.jpg)
][(lim[)]()([lim.3
n)PenjumlahaHk.()](lim[)](lim[)]()([lim2.
maka)(limdan)(limadaberikutlimitJika
.Konstanta)(Hk.lim.1
≠==
==
±=±=±
==
=
→
→
→
→→→
→→→
→→
→
M
M
L
xg
xf
xg
xf
LMxgxfxgxf
MLxgxfxgxf
MxgLxf
CC
ax
ax
ax
axaxax
axaxax
axax
ax](https://image.slidesharecdn.com/bab2-161021045042/85/materi-limit-kuliah-mahasiswa-limit-9-320.jpg)
More Related Content
What's hot (20)
Similar to materi limit kuliah mahasiswa limit (20)
More from chusnaqumillaila (10)
Recently uploaded (20)
materi limit kuliah mahasiswa limit
- 1. Bab 2. LIMIT 2.1. Dua masalah fundamental kalkulus. 2.2. Garis Tangen 2.3. Konsep Limit 2.4. Teorema Limit 2.5. Konsep kontinuitas
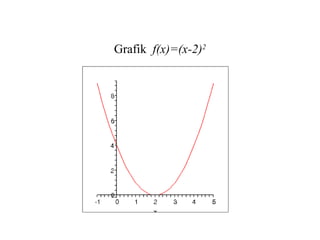
- 2. Dua Masalah Fundamental Kalkulus • Masalah 1 (Masalah Tangen): Diberikan sebuah titik P(x,f(x)) pada kurva y=f(x), bagaimana menentukan kemiringan garis tangen pada P? • Masalah 2 (Masalah Luas): Jika f(x)≥ 0 untuk x∈[a,b], bagaimana menghitung luas daerah A yaitu suatu bidang yang berada diantara kurva y=f(x) dan sumbu-x sepanjang selang [a,b]?
- 4. 2.2. Garis Tangen • Misalkan diberikan suatu fungsi f(x), maka kemiringan garis tangen L di titik P(a, f(a)) pada kurva y=f(x) dapat diaproksimasi dengan kemiringan garis secant antara titik P dan titik Q(a+h, f(a+h)). • Bila Q dibuat mendekati P dgn menelusuri kurva y=f(x) dan h menuju 0, maka diperoleh kemiringan garis tangen kurva y=f(x) di titik P(a,f(a)): ).0(, )()( ≠−+ = ∆ ∆ = h h afhaf x y mPQ h afhaf m h )()( lim 0 −+ = →
- 5. 2.3 Konsep Limit Definisi Intuitif Misalkan y=f(x) suatu fungsi, a dan L bilangan riil sedemikian hingga: • Bila x dekat a tetapi tidak sama dg a (x≠a), f(x) dekat ke L • Bila x mendekati a tetapi x≠a, maka f(x) mendekati L • Misalkan f(x) dapat kita buat sedekat mungkin ke L dg membuat x cukup dekat a tetapi tdk sama dg a • Maka dapat dikatakan bhw limit f(x) bila x mendekati a adalah L, Lxf ax = → )(lim
- 11. 2.4. Teorema2 Limit 1. Teorema Limit trigonometri: 2. Hukum Apit: Misalkan f(x) ≤ g(x) ≤ h(x) untuk semua x disekitar a namun x≠a, dan maka 1 sin lim 0 = → x x x )(lim)(lim xhLxf axax →→ == Lxg ax = → )(lim
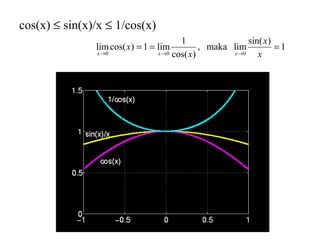
- 12. cos(x) ≤ sin(x)/x ≤ 1/cos(x) 1 )sin( limmaka, )cos( 1 lim1)cos(lim 000 === →→→ x x x x xxx
- 13. Contoh .0 1 sinlimTunjukkan 2 0x = → x x 0dan1 1 sin1,0Untuk 2 >≤≤−≠x x x 222 1 sin x x xx ≤≤− Apit).Prinsipan(menggunak0 1 sinlimmaka 0limdan0)lim(karena 2 0 2 0 2 0 = ==− → →→ x x xx x xx Bukti:
- 14. • Limit kiri (limit f(x) bila x menuju a dari kiri) • Limit kanan (limit f(x) bila x menuju a dari kanan) • Teorema 2: jika dan hanya jika Lxf ax =− → )(lim Lxf ax =+ → )(lim )(lim)(lim xfLxf axax +− →→ == Lxf ax = → )(lim
- 18. • Definisi Limit. Limit dari f(x) bila x menuju a adalah L∈ R, ditulis jika dan hanya jika, untuk ε > 0, terdapat δ > 0 sedemikian sehingga jika 0 < |x - a| < δ maka |f(x) - L| < ε. Lxf ax = → )(lim