![簡単 例
平均 求 場合
F : 未知 確率分布
? : F 平均 知 。? = T(F) = EF [X]
x = {12, 15, 16, 17, 19, 20, 22, 23, 25, 28}
F 抽出 10 個 標本
Fn : 既知 経験分布関数
10 個 標本 x 構成
?n : ? 推定値 用 統計量
?n = T(Fn) = 1
n
∑n
i=1 xi = 19.7
?n 変動 、
?n 分布 Gn 持 。（?n ～ Gn）
11 / 31](https://image.slidesharecdn.com/zansabootstrappubric-131202101208-phpapp02/85/Zansa-17-11-320.jpg)
![Mathematica code
bootstrap[func_ , dat_ , num_] :=
Table[func[ RandomChoice [dat , Length[dat ]]], {i, num }]
data = {12, 15, 16, 17, 19, 20, 22, 23, 25, 28};
boot = bootstrap[Mean , data , 2000];
Histogram[boot , Automatic]
In [289]:= N[Mean[boot ]]
Out [289]= 19.6897
16 18 20 22 24 26
50
100
150
200
250
300
18 / 31](https://image.slidesharecdn.com/zansabootstrappubric-131202101208-phpapp02/85/Zansa-17-18-320.jpg)
![標本 抽出
Γ(5, 2) 標本 30 個抽出 、
最尤推定
In [304]:= dat = RandomReal[ GammaDistribution [5, 2], 30];
edist = FindDistributionParameters [dat ,
GammaDistribution [α, β]]
Out [305]= {α -> 7.05494 , β -> 1.41704}
＿人人人人人人人人＿
＞? 違 ?＜
￣Y^Y^Y^Y^Y^Y^Y￣
23 / 31](https://image.slidesharecdn.com/zansabootstrappubric-131202101208-phpapp02/85/Zansa-17-23-320.jpg)
![推定量
標本 2000 組抽出 、
推定 。
In [432]:=
Fgamma[dat_] :=
FindDistributionParameters [dat ,
GammaDistribution [α, β]]
boot = bootstrap[Fgamma , dat , 2000];
Mean[boot [[All , All , 2]]]
Out [434]={7.95611 , 1.34972}
↑ 2000 組 推定値 α, β 平均
26 / 31](https://image.slidesharecdn.com/zansabootstrappubric-131202101208-phpapp02/85/Zansa-17-26-320.jpg)
![計算
推定 誤差 捉 、 計算
推定量 θn
b(Fn) = EFn (θ?
n) ? θn
≈
1
B
B∑
b=1
θ?
n(b) ? θn
In [443]:= nvalue = Fgamma[dat]
bias = Mean[boot [[All , All , 2]]] - nvalue [[All , 2]]
Out [443]= {0.901169 , -0.067321}
α 0.901169, β ?0.067321
27 / 31](https://image.slidesharecdn.com/zansabootstrappubric-131202101208-phpapp02/85/Zansa-17-27-320.jpg)
![推定量 修正
偏 修正済推定量
?θ = θn ? b(Fn)
= 2θn ? EFn (θ?
n)
In [443]:= nvalue [[All , 2]] - bias
Out [444]= {6.15377 , 1.48436}
偏 修正済推定量 、(α, β) = (6.15377, 1.48436)
28 / 31](https://image.slidesharecdn.com/zansabootstrappubric-131202101208-phpapp02/85/Zansa-17-28-320.jpg)
![偏 修正済推定量 分布
偏 修正済推定量
temp = Table[dat = RandomReal[ GammaDistribution [5, 2], 30];
boot = bootstrap[Fgamma , dat , 100];
nvalue = Fgamma[dat];
bias = Mean[boot [[All , All , 2]]] - nvalue [[All , 2]];
nvalue [[All , 2]] - bias , {i, 100}];
3 4 5 6 7 8 9 10
10
20
30
40
α : 平均 4.98765
分散 1.38136
1.0 1.5 2.0 2.5 3.0
10
20
30
40
β : 平均 1.96953
分散 0.203531
29 / 31](https://image.slidesharecdn.com/zansabootstrappubric-131202101208-phpapp02/85/Zansa-17-29-320.jpg)
【Zansa】第17回 ブートストラップ法入門
- 1. 法入門 @ksmzn 第 17 回 Zansa 27 Novenber 2013 1 / 31
- 2. 誰 Twiiter : @ksmzn 専門 : 計算機統計 2 / 31
- 3. 本日 ！ 3 / 31
- 4. 4 / 31
- 5. ！ 5 / 31
- 6. 法！！ 6 / 31
- 7. 法 ？ 法（Bootstrap Method） 、 n 個 標本 x1, x2, ..., xn 繰 返 許 n 個 標本 B 組選 、平均 分散 推定値 繰 返 求 、 分布 確率分布 誤差 推定 方法 7 / 31
- 8. 法 ！！ 8 / 31
- 9. 前提 、統計量 標本分布！ 定義 F : 未知 確率分布 θ : F 関 興味 θ = T(F) 表 Fn : 既知 経験分布関数 F 抽出 n 個 標本 X 構成 θn : θ 推定値 用 統計量 θn = T(FN ) 表 θn 変動 、 θn 分布 Gn 持 。（θn ～ Gn） 9 / 31
- 10. 例 考 ！ 10 / 31
- 11. 簡単 例 平均 求 場合 F : 未知 確率分布 ? : F 平均 知 。? = T(F) = EF [X] x = {12, 15, 16, 17, 19, 20, 22, 23, 25, 28} F 抽出 10 個 標本 Fn : 既知 経験分布関数 10 個 標本 x 構成 ?n : ? 推定値 用 統計量 ?n = T(Fn) = 1 n ∑n i=1 xi = 19.7 ?n 変動 、 ?n 分布 Gn 持 。（?n ～ Gn） 11 / 31
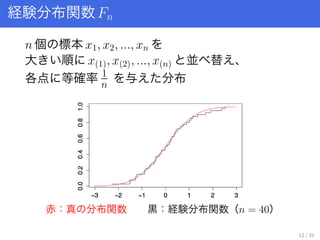
- 12. 経験分布関数Fn n 個 標本 x1, x2, ..., xn 大 順 x(1), x(2), ..., x(n) 並 替 、 各点 等確率 1 n 与 分布 赤：真 分布関数 黒：経験分布関数（n = 40） 12 / 31
- 13. 経験分布関数Fn ！ → x 復元抽出 ！ 13 / 31
- 14. 標本 例 n = 10 標本 x = {12, 15, 16, 17, 19, 20, 22, 23, 25, 28} 10 個 復元抽出 x? (1) = {20, 19, 20, 23, 19, 28, 23, 28, 17, 25} 一度 10 個 復元抽出 x? (2) = {15, 23, 12, 17, 23, 25, 16, 22, 25, 25} 14 / 31
- 15. 標本 経験分布関数 Fn 標本 。 x1, x2, ..., xn n 個 復元抽出 得 x? = {x? 1, x? 2, ..., x? n} 構成 経験分布関数 F? n 15 / 31
- 16. 標本 平均 標本 平均 x = {12, 15, 16, 17, 19, 20, 22, 23, 25, 28} → ?n = 1 n ∑n i=1 xi = 19.7 x? (1) = {20, 19, 20, 23, 19, 28, 23, 28, 17, 25} → ?? 1 = 1 n ∑n i=1 x? i (1) = 22.2 x? (2) = {15, 23, 12, 17, 23, 25, 16, 22, 25, 25} → ?? 2 = 1 n ∑n i=1 x? i (2) = 20.3 16 / 31
- 17. 推定量 分布 ?? 1 = 22.2, ?? 2 = 20.3, ?? 3 = 19.5, ... 標本 取 平均値 変 、 推定量 ?? 分布 G? n 。 ↓ 標本 平均 B = 2000 回 作 、 作 ！！ 17 / 31
- 18. Mathematica code bootstrap[func_ , dat_ , num_] := Table[func[ RandomChoice [dat , Length[dat ]]], {i, num }] data = {12, 15, 16, 17, 19, 20, 22, 23, 25, 28}; boot = bootstrap[Mean , data , 2000]; Histogram[boot , Automatic] In [289]:= N[Mean[boot ]] Out [289]= 19.6897 16 18 20 22 24 26 50 100 150 200 250 300 18 / 31
- 19. 法 流 1 母集団 F 大 n 標本 抽出 2 標本 興味 θn 求 3 標本 復元抽出 B 回繰 返 標本 4 推定値 求 、 信頼区間 求 19 / 31
- 20. 法 考 方 法 以下 置 換 未知 確率分布 F ? 経験分布関数 Fn F 関 θ = T(F) ? Fn 関 θn = T(Fn) 推定量 θn = T(Fn) ? 推定量 分布 Gn θ? n = T(F? n ) 分布 G? n 未知 F 標本 何度 抽出 、 既知 Fn 。 20 / 31
- 21. 適用例 分布Γ(α, β) 推定 ！ 21 / 31
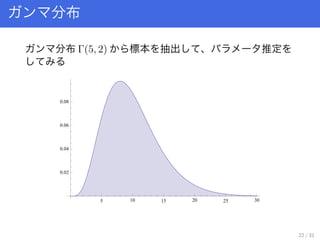
- 22. 分布 分布 Γ(5, 2) 標本 抽出 、 推定 5 10 15 20 25 30 0.02 0.04 0.06 0.08 22 / 31
- 23. 標本 抽出 Γ(5, 2) 標本 30 個抽出 、 最尤推定 In [304]:= dat = RandomReal[ GammaDistribution [5, 2], 30]; edist = FindDistributionParameters [dat , GammaDistribution [α, β]] Out [305]= {α -> 7.05494 , β -> 1.41704} ＿人人人人人人人人＿ ＞? 違 ?＜ ￣Y^Y^Y^Y^Y^Y^Y￣ 23 / 31
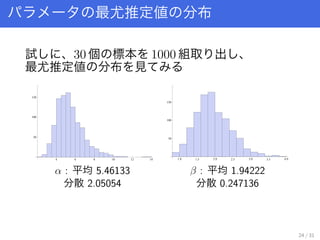
- 24. 最尤推定値 分布 試 、30 個 標本 1000 組取 出 、 最尤推定値 分布 見 4 6 8 10 12 14 50 100 150 α : 平均 5.46133 分散 2.05054 1.0 1.5 2.0 2.5 3.0 3.5 4.0 50 100 150 β : 平均 1.94222 分散 0.247136 24 / 31
- 25. 母集団 何度 、 現実的 難 。 ↓ 標本 ！ 25 / 31
- 26. 推定量 標本 2000 組抽出 、 推定 。 In [432]:= Fgamma[dat_] := FindDistributionParameters [dat , GammaDistribution [α, β]] boot = bootstrap[Fgamma , dat , 2000]; Mean[boot [[All , All , 2]]] Out [434]={7.95611 , 1.34972} ↑ 2000 組 推定値 α, β 平均 26 / 31
- 27. 計算 推定 誤差 捉 、 計算 推定量 θn b(Fn) = EFn (θ? n) ? θn ≈ 1 B B∑ b=1 θ? n(b) ? θn In [443]:= nvalue = Fgamma[dat] bias = Mean[boot [[All , All , 2]]] - nvalue [[All , 2]] Out [443]= {0.901169 , -0.067321} α 0.901169, β ?0.067321 27 / 31
- 28. 推定量 修正 偏 修正済推定量 ?θ = θn ? b(Fn) = 2θn ? EFn (θ? n) In [443]:= nvalue [[All , 2]] - bias Out [444]= {6.15377 , 1.48436} 偏 修正済推定量 、(α, β) = (6.15377, 1.48436) 28 / 31
- 29. 偏 修正済推定量 分布 偏 修正済推定量 temp = Table[dat = RandomReal[ GammaDistribution [5, 2], 30]; boot = bootstrap[Fgamma , dat , 100]; nvalue = Fgamma[dat]; bias = Mean[boot [[All , All , 2]]] - nvalue [[All , 2]]; nvalue [[All , 2]] - bias , {i, 100}]; 3 4 5 6 7 8 9 10 10 20 30 40 α : 平均 4.98765 分散 1.38136 1.0 1.5 2.0 2.5 3.0 10 20 30 40 β : 平均 1.96953 分散 0.203531 29 / 31
- 30. 法 、標本 多数回 行 推定 未知 確率分布 既知 経験分布 置 換 母集団 場合 、 計算機 統計量 偏 （ 分散、 対 信頼区間） 構成 30 / 31
- 31. 。 31 / 31