Лекц?я冲1
- 1. Лекц?я № 1 Суть задач? вир?внювання дек?лькох вим?ряних величин. Метод найменших квадрат?в. МЕТОДИ ВИР?ВНЮВАННЯ БАГАТЬОХ ВИМ?РЯНИХ ВЕЛИЧИН ЗМ1 ПАРАМЕТРИЧНИЙ МЕТОД ВИР?ВНЮВАННЯ
- 2. 1. Сутн?сть задач? зр?внювання результат?в вим?р?в у геодез?? ?люстрац?я нев’язок при вим?рюванн? трьох кут?в трикутника Вираз γ = 180° – α – β справедливий т?льки для д?йсних значень кут?в α ? β трикутника. Але, оск?льки ц? величини вим?р?в м?стять похибки, то вони можуть привести або до ?х частково? компенсац??, або до грубо? похибки. Виника? ситуац?я невизначеност?, яку вир?шують шляхом надлишкових вим?р?в. Виника? завдання знаходження поправок до вим?ряних величин, як? б м?н?м?зували сумарну похибку вим?р?в, тобто зр?внювання вим?ряних величин.
- 3. Зр?внювання геодезичних вим?р?в це сукупн?сть математичних операц?й, що виконуються для набуття най?мов?рн?шого значення геодезичних координат точок земно? поверхн? ? для оц?нки точност? результат?в вим?р?в. Зр?внювання (вр?вноваження) проводиться шляхом визначення поправок до вим?ряних величин (кут?в, напрямк?в, довжин л?н?й, перевищень тощо). Вр?вноважене значення для величини Xi запису?ться де: xi – вим?ряне значення величини Xi, vi – поправка до результату вим?рювання Зр?внювання геодезичних побудов викону?ться в тих випадках, коли: 1) в?дом? вих?дн? дан?, яких вистача? для обчислення параметр?в побудови, що визначаються; 2) виконано n вим?р?в, причому n>k (k – число необх?дних вим?р?в); 3) серед вим?ряних n елемент?в побудови ? k величин, як? необх?дн? ? достатн? для визначення шуканих параметр?в. nivx ii ,1, ??
- 4. Зр?внювання под?ляють на: строге (для обробки високоточних ? точних геодезичних вим?рювань) - поправки зазвичай визначають за допомогою методу найменших квадрат?в так, щоб сума квадрат?в вс?х поправок була найменшою. Поправки такого зр?внювання мають най?мов?рн?ш? (оптимальн?) значення. спрощене (нестроге) - вс? геометричн? умови виконуються, а най?мов?рн?ше значення величин ? оц?нку точност? набувають приблизно. Застосування методу найменших квадрат?в до зр?внювання вим?ряних величин справедливо т?льки у тому випадку, коли похибки ?х мають випадковий характер! Зр?внювання забезпечу?: 1) однозначне визначення параметр?в геодезично? побудови; 2) п?двищення точност? визначення елемент?в ? параметр?в побудови.
- 5. Як при строгому, так ? при спрощеному зр?внюванн? головним чином використовуються два способи: 1) спос?б умовних вим?р?в - поправки в?дшукують безпосередньо до вим?ряних величин 2) спос?б посередн?х вим?р?в - поправки в?дшукують до функц?й вим?ряних величин (наприклад до координат при вим?ряних кутах). Будь-який спос?б зр?внювання склада?ться з наступних основних етап?в: - попередн? обчислення; - складання умовних р?внянь або р?внянь похибок; - вир?шення нормальних р?внянь; - оц?нка точност? вим?ряних ? зр?вняних величин.
- 6. Засоби вир?шення систем нормальних р?внянь 1) За допомогою обчислювального блоку у середовищ? MathCAD 2) За допомогою функц?й роботи з матрицями у середовищ? Excel - матричний запис системи р?внянь, де A – матриця коеф?ц??нт?в р?внянь, В – матриця в?льних член?в, Х – матриця нев?домих Для знаходження вектора Х необх?дно: 1) Ввести в д?апазони ком?рок матрицю А ? вектор В; 2) Знайти з допомогою функц?? МОБР(масив) обернену матрицю А-1 ; 3) За допомогою функц?? МУМНОЖ(масив1;масив2) знайти добуток матрицю А-1 на вектор В. Результат буде шуканим вектором Х. 3) За допомогою спец?альних програм ? модул?в , наприклад CredoDAT , Geonics, StarNet, IndorSurvey тощо.
- 7. 2. Два п?дходи до розв’язання задач? зр?внювання геодезичних побудов Багаторазов?, у тому числ? ? надлишков? вим?ри в задачах зр?внювання, формально представляються у вигляд? системи р?внянь, яку можна розглядати як модель сер?? вим?р?в. Як правило, процеси вим?р?в описуються невизначеними системами р?внянь: - недовизначеною системою – система, число р?внянь в як?й менше числа нев?домих; - перевизначеною системою – система, число р?внянь яко? б?льше числа нев?домих.
- 8. β1 β2 β3 Приклади систем р?внянь 1) недовизначена система 2) перевизначена система де β – вим?рян? кути, V – поправки до вим?р?в. де W – нев'язка в трикутнику Отримане р?вняння м?стить три нев?домих V1, V2, V3 ? один в?льний член W. Таке р?вняння ма? безл?ч р?шень, тобто система р?внянь, що склада?ться з одного р?вняння ? недовизначеною. Задано систему трьох н?вел?рних ход?в з одн??ю вузловою точкою С, висота яко? Н – нев?дома, Н1, Н2, Н3 – висоти репер?в, h1, h2, h3 – вим?рян? перевищення. Система трьох р?внянь з одним нев?домим ? перевизначеною ? також ма? безл?ч р?шень.
- 9. 3. Сутн?сть ? об?рунтування методу найменших квадрат?в, його використання у зр?внюванн? геодезичних побудов. Метод вир?шення невизначених систем р?внянь був запропонований на початку XIX ст. н?мецьким математиком ? геодезистом К.Ф. Гауссом ? французьким математиком А.М. Лежандром, отримавши отримав назву методу найменших квадрат?в (МНК). МНК - один з метод?в регрес?йного анал?зу, призначений для оц?нки нев?домих величин за результатами вим?р?в, що м?стять випадков? похибки. В?н застосову?ться також для наближеного представлення задано? функц?? ?ншими (прост?шими) функц?ями.
- 10. Суть вир?шення невизначених систем р?внянь, що описують деяку геодезичну побудову поляга? в тому, що на них накладаються умови м?н?м?зац?? для р?вноточних вим?р?в для нер?вноточних вим?р?в де p – ваги вим?р?в, v – поправка вим?р?в умова методу найменших квадрат?в у матричному вигляд?
- 11. Об?рунтування використання МНК у зр?внюванн? геодезичних побудов (Ф.Р. Гельмерт, XIX ст.) 1. Якщо результати вим?р?в м?стять лише випадков? похибки, що п?дкоряються нормальному закону розпод?лу, то значення нев?домих, отриман? методом найменших квадрат?в будуть най?мов?рн?шими значеннями нев?домих ? волод?тимуть найменшою середньою квадратичною похибкою. 2. Якщо результати вим?р?в м?стять похибки, що волод?ють т?льки властивостями компенсац??, значення нев?домих, хоча ? матимуть найб?льшу вагу, але не можуть вважатися за най?мов?рн?ш? значення нев?домих. 3. Якщо результати вим?р?в окр?м випадкових, сутт?во обтяжен? систематичними похибками, то зр?внювання вим?р?в методом найменших квадрат?в дасть, як завжди однозначне розв'язання, але знайден? значення не будуть най?мов?рн?шими ? не волод?тимуть найб?льшою вагою.
- 12. На сьогодн? ?сну? велика р?зноман?тн?сть способ?в зр?внювання, як? як правило ? модиф?кац?ями параметричного ? корелатного: комб?нований, рекурентний, параметричний спос?б ?з залежними зм?нними, корелатний спос?б з додатковими параметрами, спос?б посл?довних наближень та ?нш?. Вир?внювання геодезично? мереж? параметричним та корелатним чи пох?дними методами приводить завжди до однакових результат?в! Виб?р способу зр?внювання об?рунтову?ться найменшим об'?мом обчислень, необх?дним для його реал?зац??. Невизначен?сть систем р?внянь, що описують процеси вим?р?в, а також роз'яснення Гельмерта зумовили появу двох основних способ?в зр?внювання геодезичних побудов, як? найчаст?ше застосовуються у геодезичн?й практиц?: 1) параметричний спос?б, що застосову?ться у випадку, якщо невизначен?сть системи р?внянь носить перевизначений характер; 2) корелатний спос?б (спос?б зр?внювання вим?ряних величин, зв'язаних деякими умовами), якщо система р?внянь ? недовизначеною.
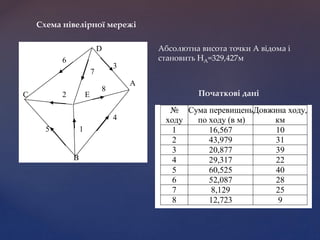
- 13. А Е В С D 1 2 3 4 5 6 7 8 Схема н?вел?рно? мереж? Абсолютна висота точки А в?дома ? становить НА=329,427м № ходу Сума перевищень по ходу (в м) Довжина ходу, км 1 16,567 10 2 43,979 31 3 20,877 39 4 29,317 22 5 60,525 40 6 52,087 28 7 8,129 25 8 12,723 9 Початков? дан?