![ロボット制御での強化学習
5
? 方策：状態??が観測したもとで行動??を選択する条件付き確率分布
? 報酬関数：状態??で行動??をとり、次の状態???に遷移した時の報酬??
? 強化学習の目的：報酬和の期待値を最大化する方策???
を獲得
出力：行動??入力：状態??
センサ
アクチュエータ
?? ??|??
報酬??
環境
?? = ?? ??, ??, ???
???
= argmax
??
Ε
?? ????|????
????(????+1|????,????)
?
??=0
∞
????
?? ????
, ????
, ????+1 ?? ∈ (0,1] ：割引率
遠い先の報酬ほど割り引く
方策?? ??|??](https://image.slidesharecdn.com/ai20187rlapplication-181126055531/85/2018-5-320.jpg)
人工知能2018 强化学习の応用
- 1. 人工知能 第7回 强化学习の応用 2018年6月1日 八谷 大岳 1
- 3. 構成 3 ? 强化学习の基础の復習 ? データを用いた価値関数の最適化 ? 行動価値関数とQテーブル ? Q学習 ? Q学習の実装例 ? openAIを用いたQ学習の実装?実行例 ? その他 ? 方策オン型の方策反復法
- 4. 機械学習手法の種類 4 ? 問題（データの条件など）と目的に合わせて適切な 機械学習方法を選択する必要がある 問題 定義 代表的な方法 応用例 教師あり学習 入力と出力のデータに基づき、 入力を出力に変換する関数を 学習 SVM, 最小二乗法、 決定木、ランダム フォーレストなど スパム分類、顔検出、一 般物体認識、将棋局面 の評価など 教師なし学習 入力のみのデータに基づき、 入力の特性 （パターン、構造） を学習 PCA, LDA、HMMなど データの可視化 （クラスタリング、次元圧 縮） 半教師学習 入力のうち部分的に付与された 出力の事例に基づき 入力を出力に変換する関数を 学習 transductiveSVM, Laplacian SVMなど 画像、音声、Webログな どの大量データで、コス トの問題で一部のデータ のみしか出力（答え）が 付与されていない場合 強化学習 入力と、出力に対する報酬 （評価）のデータに基づき、 入力を出力に変換する関数を 学習 Q-learning、policy iteration, policy gradient ロボット制御、Web広告 選択、マーケティング
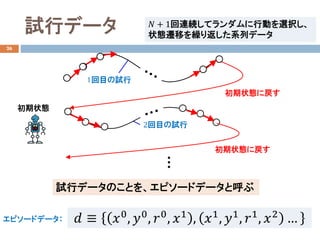
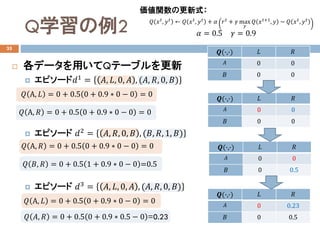
- 5. ロボット制御での強化学習 5 ? 方策：状態??が観測したもとで行動??を選択する条件付き確率分布 ? 報酬関数：状態??で行動??をとり、次の状態???に遷移した時の報酬?? ? 強化学習の目的：報酬和の期待値を最大化する方策??? を獲得 出力：行動??入力：状態?? センサ アクチュエータ ?? ??|?? 報酬?? 環境 ?? = ?? ??, ??, ??? ??? = argmax ?? Ε ?? ????|???? ????(????+1|????,????) ? ??=0 ∞ ???? ?? ???? , ???? , ????+1 ?? ∈ (0,1] ：割引率 遠い先の報酬ほど割り引く 方策?? ??|??
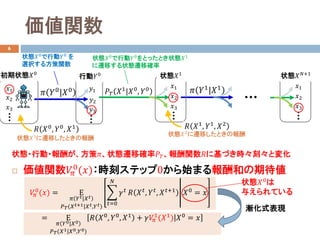
- 6. 価値関数 6 ? 価値関数???? 0 (??)：時刻ステップ0から始まる報酬和の期待値 ???? 0 (??) = Ε ?? ????|???? ????(????+1|????,????) ?? ??=0 ?? ???? ?? ????, ????, ????+1 ??0 = ?? = Ε ?? ??0|??0 ????(??1|??0,??0) |?? ??0 , ??0 , ??1 + ?????? 1 (??1 ) ??0 = ?? 漸化式表現 ???? ??1|??0, ??0 状態??0 で行動??0 をとったとき状態??1 に遷移する状態遷移確率 状態??1 ??1 ??2 ??3 ?? ??0|??0 状態??0 で行動??0 を 選択する方策関数 ??1 行動??0 ??2 ??3 ?? ??1 |??1 状態??1 に遷移したときの報酬 ??1 ??2 ??3 初期状態??0 ?? ??1 , ??1 , ??2 状態?? ??+1 ??1 ??2 ??3 ?? ??0 , ??0 , ??1 状態??2 に遷移したときの報酬 状態?行動?報酬が、方策??、状態遷移確率????、報酬関数??に基づき時々刻々と変化 状態??0 は 与えられている
- 7. 演習1 7 1. 顧客の「年齢」と「収入」のデータを活用して、以下の分析を 行いたい。それぞれ適切な機械学習手法を選択しなさい。 2. 強化学習を選択した場合は、状態?? 、行動?? 、および報酬?? を定義しなさい ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の一 番上に記載 「年齢」から「収入」を予測したい 「年齢と収入」から似ている回答者を グループ化したい 顧客に送る、商品のダイレクト メールを選択をしたい 教師あり学習 教師なし学習 強化学習 機械学習の手法
- 8. 価値の列挙法 12 ? 決定的な方策と、価値を列挙し、最大価値の方策を選択 ? 必要な演算数（価値関数の計算回数） ? 3ステップ2状態チェインウォークの場合：（2×2）×（2×3）＝24回 ? 実問題では状態数が膨大 なので計算量が爆発 （状態数×行動数） × （状態数 × ステップ数） 方策の数 各方策で計算する価値の数 ゲーム 局面の数 将棋 10の226乗 囲碁 10の360乗 方策 価値 ??1 ????1 0 ?? = 0, ????1 0 ?? = 2.71 ??2 ????2 0 ?? = 0, ????2 0 ?? = 0 ??3 ????3 0 ?? = 0, ????3 0 ?? = 0 ??4 ????4 0 ?? = 1.71, ????4 0 ?? = 2.71 最大の価値を持つ方策関数??4を選択 状態：?? ∈ A,B 行動：?? ∈ L, R ?? B L R RL 報酬関数：?? ??, ??, B = 1 割引率：γ = 0.9 ステップ数：?? = 2 初期状態確率：???? A = 1 ??1 ?? = ?? ?? = ?? = 1 ??1 ?? = ?? ?? = ?? = 1 ??2 ?? = ?? ?? = ?? = 1 ??2 ?? = ?? ?? = ?? = 1 ??3 ?? = ?? ?? = ?? = 1 ??3 ?? = ?? ?? = ?? = 1 ??4 ?? = ?? ?? = ?? = 1 ??4 ?? = ?? ?? = ?? = 1 スキップ>>
- 9. 動的計画法 13 ? 価値関数の最大化を2ステップずつ解く ? ??ステップ目の価値を計算し、最大の価値????? ?? ?? を選択 ? 次の1と2を?? = ?? ? 1, ?? ? 2, … , 2,1,0と繰り返す 1. ??ステップの価値???? ?? (??)を、 ??+1ステップの最大価値????? ??+1 ?? を用いて計算 2. 最大の価値????? ?? ?? を選択 ???? ?? (??) = Ε ?? ?? ??|???? ????(????+1|????,????) |?? ????, ????, ????+1 + ??????? ??+1 (????+1) ????+1 = ?? ???? ?? (??) = Ε ?? ?? ??|?? ?? ????(?? ??+1|?? ??,?? ??) |?? ?? ??, ?? ??, ?? ??+1 ?? ?? = ?? スキップ>>
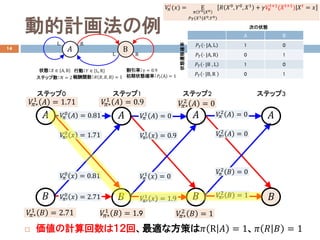
- 10. 動的計画法の例 14 ? 価値の計算回数は１２回、最適な方策は?? R ?? = 1、?? ?? ?? = 1 ???? 2 ?? = 0 ????′ 2 ?? = 0 ?? ステップ2 ?? ????′ 2 ?? = 1 ???? 2 ?? = 0 ????? 2 ?? = 0 ???? 1 ?? = 0 ????′ 1 ?? = 0.9 ????′ 1 ?? = 1.9 ???? 1 ?? = 0 ????? 1 ?? = 1.9 ????? 1 ?? = 0.9 ????? 2 ?? = 1 ?? ?? ステップ3 ?? ?? ステップ1 ???? 0 ?? = 0.81 ????′ 0 ?? = 1.71 ????′ 0 ?? = 2.71 ???? 0 ?? = 0.81 ????? 1 ?? = 2.71 ????? 1 ?? = 1.71 ?? ?? ステップ0 状態：?? ∈ A,B 行動：?? ∈ L, R ?? B L R RL 報酬関数：?? ??, ??, B = 1 状態遷移確率 割引率：γ = 0.9 次の状態 ステップ数：?? = 2 初期状態確率：???? A = 1 ???? ?? (??) = Ε ?? ??0|??0 ????(??1|??0,??0) |?? ??0 , ??0 , ??1 + ?????? ??+1 (????+1 ) ???? = ?? A B ???? ? |A, L 1 0 ???? ? |A, R 0 1 ???? ? |B , L 1 0 ???? ? |B, R 0 1
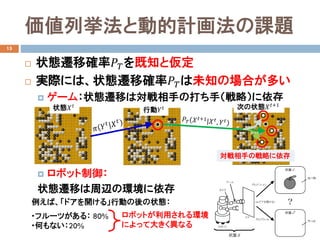
- 11. 価値列挙法と動的計画法の課題 15 ? 状態遷移確率????を既知と仮定 ? 実際には、状態遷移確率????は未知の場合が多い ? ゲーム：状態遷移は対戦相手の打ち手（戦略）に依存 ? ロボット制御： 状態遷移は周辺の環境に依存 状態???? 行動???? 例えば、「ドアを開ける」行動の後の状態： ロボットが利用される環境 によって大きく異なる ?フルーツがある： 80% ?何もない：20% 次の状態????+1 対戦相手の戦略に依存
- 12. 強化学習手法の一覧 16 ? 価値列挙と動的計画以外にも様々な手法がある 方法 遷移確率 概要 価値列挙法 動的計画法 など 既知 遷移確率関数????に基づき、方策関数 の候補??1、??2、 … の価値関数????1 ?? (??)、????2 ?? (??)、… を 漸化式を活用して計算。最大の価値を持つ方策??? を選択。 モンテカルロ法、 TD法、TD(λ)法 SARSA法、Q学習法 最小二乗TD法など 未知 方策???? に従いランダムに行動を選択し、データを 収集。データを用いて行動価値関数???? ?? (??, ??)を改善 し、最適な行動関数??? ?? (??, ??)を獲得。 方策勾配法 貪欲方策勾配法 パラメータベース方策 探索法など 未知 方策????に従いランダムに行動を選択し、データを 収集。データを用いて方策関数????(??|??)を改善し、 最適な方策関数???(??|??)を獲得。 今回は将棋や囲碁で実績のあるQ学習法を紹介
- 13. 構成 17 ? 强化学习の基础の復習 ? データを用いた価値関数の最適化 ? 行動価値関数とQテーブル ? Q学習 ? Q学習の実装例 ? openAIを用いたQ学習の実装?実行例 ? その他 ? 方策オン型の方策反復法
- 14. 行動価値関数 18 ? 行動価値関数： Q関数と呼ばれる価値関数??の拡張版 ? 状態??で行動??を取った後、方策??に従った場合に将来得られる報酬和期待値 ? Q関数：状態??で行動??を選択する方策?? ??|?? を求めるのに用いられる ???? (??, ??) = Ε ?? ?? ??|?? ?? ????(?? ??+1|?? ??,?? ??) ?? ??=0 ∞ ???? ?? ???? , ???? , ????+1 ??0 = ??, ??0 = ?? 強くなるロボティック?ゲームプレイヤーの作り方 八谷、杉山 2016 ???? (???? , ???? = ??1) ????状態 ????(????, ???? = ??2) ????(????, ???? = ??3) 状態???? で行動??1を取る価値 ???? ???? |?????1 , ?????1 状態??0 と行動??0 は 与えられている ???? ????+1 |???? , ???? 行動 ??1の価値： ??2の価値： ??3の価値： ???? 状態???? で行動??3を取る価値最大の価値の行動を 高い確率で選択! ?? ???? |???? どの行動？
- 15. 行動価値関数のテーブル表現 20 ? 状態と行動が有限でかつ離散的と仮定した単純な表現方法 ? 行に状態、列に行動、各要素に状態と行動の組に対する価値 ? 2状態チェインウォークの場合のQテーブルの例 ??1 ???? ? ??1 ????(??1, ??1) ????(??1, ??2) ? ??2 ????(??2, ??1) ????(??2, ??2) ? ? ? ? ? 状態の種類 行動の種類 ?? ?? ?? ?? ?? ?? 「Qテーブル」と呼ばれる ?? ?? ?? ?? ?? (??, ??) ?? ?? (??, ??) ?? ?? ?? (??, ??) ?? ?? (??, ??)
- 16. Qテーブルを用いた行動選択 21 ? 貪欲方策：最大の価値を持つ行動を選択 ? ソフトマックス方策：試行錯誤のために確率的に行動を選択 ??(??|??) = ? 1 if ?? = ??????max ??′ ??(??, ???) 0 otherwise ??(?,?) ?? ?? ?? 0.23 0.4 ?? 0.15 0.98 ??(??|??) = 1 ??(??|??) = 0 貪欲方策 ??(??|??) = 0 ??(??|??) = 1 ??(??|??) = exp(?? ??, ?? ) ∑??? exp(?? ??, ??′ ) ??(?,?) ?? ?? ?? 0.23 0.4 ?? 0.15 0.98 ソフトマックス ??(??|??) = 0.54 ??(??|??) = 0.3 ??(??|??) = 0.46 ??(??|??) = 0.7
- 17. 演習2 22 ? 以下のQテーブルに基づき、貪欲方策と ソフトマックス方策を求めなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を 用紙の 一番上に記載 ??(?,?) ?? ?? ?? 0.98 0.15 ?? 0.64 0.32
- 18. 構成 24 ? 强化学习の基础の復習 ? データを用いた価値関数の最適化 ? 行動価値関数とQテーブル ? Q学習 ? Q学習の実装例 ? openAIを用いたQ学習の実装?実行例 ? その他 ? 方策オン型の方策反復法
- 19. 動物の行動学習：試行錯誤学習 25 ? 心理学の行動主義者の学習の定義 ? 行動や反応の変化として表れ、外部から観察できる現象 ? 試行錯誤学習 Edward Thorndike（1874年?1949年） 迷路のような箱の中で，猫は試行錯誤的に様々な行動を取る。 偶然にでも外に出る行動を取り，それを何度か繰り返すと， やがて同じ行動が出現する頻度が高くなることを実験的に確認 猫が様々な行動をとる 偶然に外に出られた 強くなるロボティック?ゲームプレイヤーの作り方 八谷、杉山 2016 また箱にいれる 試行錯誤の過程を経て何度か繰り返すと、やがて同じ行動が出現する頻度が高くなる 【猫の問題箱実験】 行動後の「満足」または「不快」の度合いに応じて、 行動の出現頻度が学習の過程を経て変化
- 20. 試行データ 26 ?? ≡ ??0 , ??0 , ??0 , ??1 , ??1 , ??1 , ??1 , ??2 …エピソードデータ： 1回目の試行 2回目の試行 ?? + 1回連続してランダムに行動を選択し、 状態遷移を繰り返した系列データ 試行データのことを、エピソードデータと呼ぶ 初期状態 初期状態に戻す 初期状態に戻す
- 21. エピソードデータの例 27 ? 5回の試行によるエピソードデータの例（?? = 1の場合） ??1 = ??, ??, 0, ?? , (??, ??, 0, ??) 状態：?? ∈ ??, ?? 行動：?? ∈ ??, ?? ?? ?? ?? ?? ?? ?? 報酬関数：?? ??, ??, ?? = 1 状態遷移確率 割引率：γ = 0.9 次の状態 初期状態確率：???? ?? =1ステップ数：?? = 2 ??2 = ??, ??, 0, ?? , (??, ??, 1, ??) ??3 = ??, ??, 0, ?? , (??, ??, 0, ??) ??4 = ??, ??, 0, ?? , (??, ??, 0, ??) 方策??1 ?? ?? ?? ? |?? 0.5 0.5 ?? ? |?? 0.5 0.5 状態 行動 ??5 = ??, ??, 0, ?? , (??, ??, 0, ??) ランダムに試行錯誤 ?? ≡ ??0, ??0, ??0, ??1 , ??1, ??1, ??1, ??2 A B ???? ? |A, L 1 0 ???? ? |A, R 0 1 ???? ? |B , L 1 0 ???? ? |B, R 0 1
- 22. 最大行動価値関数の展開 30 ??? (??, ??) = max ?? Ε ?? ?? ??|?? ?? ????(?? ??+1|????,????) ?? ??=0 ∞ ???? ?? ???? , ???? , ????+1 ??0 = ??, ??0 = ?? = Ε ????(??1|??0,??0) ??? ??0 , ??0 , ??1 + ??max ?? Ε ?? ??1|??1 |???? ??1 , ??1 ??1 ??0 = ??, ??0 = ?? = max ?? Ε ?? ?? ??|?? ?? ????(?? ??+1|?? ??,????) ??? ??0 , ??0 , ??1 + ? ??=1 ∞ ???? ?? ???? , ???? , ????+1 ??0 = ??, ??0 = ?? = max ?? Ε ?? ?? ??|?? ?? ????(?? ??+1|?? ??,????) ??? ??0 , ??0 , ??1 + ?? ? ??=1 ∞ ?????1 ?? ???? , ???? , ????+1 ??0 = ??, ??0 = ?? = max ?? Ε ?? ??1|??1 ????(??1|??0,??0) ??? ??0 , ??0 , ??1 + ?? Ε ?? ????|???? ????(????+1|????,????) ?? ??=1 ∞ ?????1 ?? ???? , ???? , ????+1 ??1 , ??1 ??0 = ??, ??0 = ?? = max ?? Ε ????(??1|??0,??0) ??? ??0 , ??0 , ??1 + ?? Ε ?? ??1|??1 |???? ???? , ???? ??1 ??0 = ??, ??0 = ?? = max ?? Ε ?? ??1|??1 ????(??1|??0,??0) |?? ??0 , ??0 , ??1 + ?????? ??1 , ??1 ??0 = ??, ??0 = ??
- 23. Q学習法 31 ? 目的：最大行動価値関数を獲得 ? 最大行動価値関数の漸化式表現： ? Q学習法：最大行動価値関数の漸化式を満たすように、 エピソードデータを用いて以下のルールで行動価値関数を更新 ?? ????, ???? ← ?? ????, ???? + ?? ???? + ?? max ?? ?? ????+1, ?? ? ?? ????, ???? ?? ??, ?? ：方策に依存しない価値関数 ??? ??, ?? = Ε ????(??1|??0,??0) ??? ??0 , ??0 , ??1 + ??max ?? Ε ?? ??1|??1 |???? ??1 , ??1 ??1 ??0 = ??, ??0 = ?? ??：学習率、??：割引率 ???(??, ??) = max ?? ???? (??, ??) 最適な行動価値関数が求まれば、 貪欲方策により最適な方策が求まる
- 24. 演習3 32 1. 以下の１つのエピソードデータを用いて、Qテーブルを更新 する式を２つ書き、Qテーブルの値を更新しなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 ?? ???? , ???? ← ?? ???? , ???? + ?? ???? + ?? max ?? ?? ????+1 , ?? ? ?? ???? , ???? ??2 = ??, ??, 0, ?? , (??, ??, 1, ??) Qテーブルの初期値：?? ?,? = 0 学習率?? = 0.5、割引率?? = 0.9
- 25. Q学習の例 34 ? 2状態マルコフチェーン ? Q学習による価値関数の更新 価値関数の更新式： ?? = 0.5 ?? = 0.9 価値関数の初期値??(?,?) = 0 状態：?? ∈ ??, ?? 行動：?? ∈ ??, ?? ?? ?? ?? ?? ?? ?? 報酬関数：?? ??, ??, ?? = 1 状態遷移確率 割引率：γ = 0.9 次の状態 初期状態確率：???? ?? =1ステップ数：?? = 2 ??1 = ??, ??, 0, ?? , (??, ??, 0, ??) ??2 = ??, ??, 0, ?? , (??, ??, 1, ??) ??3 = ??, ??, 0, ?? , (??, ??, 0, ??) ??4 = ??, ??, 0, ?? , (??, ??, 0, ??) ??5 = ??, ??, 0, ?? , (??, ??, 0, ??) エピソードデータ： ??6 = ??, ??, 0, ?? , (??, ??, 0, ??) ??(?,?) ?? ?? ?? 0 0 ?? 0 0 ?? ???? , ???? ← ?? ???? , ???? + ?? ???? + ?? max ?? ?? ????+1 , ?? ? ?? ???? , ???? Qテーブル A B ???? ? |A, L 1 0 ???? ? |A, R 0 1 ???? ? |B , L 1 0 ???? ? |B, R 0 1
- 26. Q学習の例2 35 ? 各データを用いてQテーブルを更新 ? エピソード??1 = ??, ??, 0, ?? , (??, ??, 0, ??) ? エピソード ??2 = ??, ??, 0, ?? , (??, ??, 1, ??) ? エピソード ??3 = ??, ??, 0, ?? , (??, ??, 0, ??) ?? A, ?? = 0 + 0.5 0 + 0.9 ? 0 ? 0 = 0 ?? A, ?? = 0 + 0.5 0 + 0.9 ? 0 ? 0 = 0 ?? A, ?? = 0 + 0.5 0 + 0.9 ? 0 ? 0 = 0 ?? ??, ?? = 0 + 0.5 1 + 0.9 ? 0 ? 0 =0.5 ?? A, ?? = 0 + 0.5 0 + 0.9 ? 0 ? 0 = 0 ?? ??, ?? = 0 + 0.5 0 + 0.9 ? 0.5 ? 0 =0.23 ??(?,?) ?? ?? ?? 0 0 ?? 0 0 ??(?,?) ?? ?? ?? 0 0 ?? 0 0.5 ??(?,?) ?? ?? ?? 0 0.23 ?? 0 0.5 ??(?,?) ?? ?? ?? 0 0 ?? 0 0 価値関数の更新式： ?? = 0.5 ?? = 0.9 ?? ???? , ???? ← ?? ???? , ???? + ?? ???? + ?? max ?? ?? ????+1 , ?? ? ?? ???? , ????
- 27. Q学習の例3 36 ? 各データを用いてQテーブルを更新 ? エピソード??4 = ??, ??, 0, ?? , (??, ??, 0, ??) ? エピソード ??5 = ??, ??, 0, ?? , (??, ??, 0, ??) ? エピソード ??6 = ??, ??, 0, ?? , (??, ??, 1, ??) ??(?,?) ?? ?? ?? 0 0.34 ?? 0.15 0.5 ??(?,?) ?? ?? ?? 0.23 0.34 ?? 0.15 0.5 ??(?,?) ?? ?? ?? 0.23 0.4 ?? 0.15 0.98 ?? A, ?? = 0.23 + 0.5 0 + 0.9 ? 0.5 ? 0.23 = 0.34 ?? ??, ?? = 0 + 0.5 0 + 0.9 ? 0.34 ? 0 = 0.15 ?? A, ?? = 0 + 0.5 0 + 0.9 ? 0.34 ? 0 =0.15 ?? ??, ?? = 0.15 + 0.5 0 + 0.9 ? 0.34 ? 0.15 = 0.23 ?? A, ?? = 0.34 + 0.5 0 + 0.9 ? 0.5 ? 0.34 = 0.4 ?? ??, ?? = 0.5 + 0.5 1 + 0.9 ? 0.5 ? 0.5 = 0.98 ??(?,?) ?? ?? ?? 0 0.23 ?? 0 0.5 価値関数の更新式： ?? = 0.5 ?? = 0.9 ?? ???? , ???? ← ?? ???? , ???? + ?? ???? + ?? max ?? ?? ????+1 , ?? ? ?? ???? , ????
- 28. 課題1 37 ? 2状態チェインウォーク ? Q学習法を用いてQテーブルを更新しなさい 状態：?? ∈ ??, ?? 行動：?? ∈ ??, ?? ?? ?? ?? ?? ?? ?? 報酬関数：?? ??, ??, ?? = 1 状態遷移確率 割引率：γ = 0.9 次の状態 初期状態確率：???? ?? =1ステップ数：?? = 2 ?? ?? ?? ? |?? 0.5 0.5 ?? ? |?? 0.5 0.5 状態 行動 方策 ??1 ?? = 0.5 価値関数の初期値??(?,?) = 0 ??1 = ??, ??, 0, ?? , (??, ??, 1, ??) ??2 = ??, ??, 0, ?? , (??, ??, 0, ??) ??3 = ??, ??, 0, ?? , (??, ??, 0, ??) ??4 = ??, ??, 0, ?? , (??, ??, 0, ??) ??5 = ??, ??, 0, ?? , (??, ??, 1, ??) エピソードデータ： ??6 = ??, ??, 0, ?? , (??, ??, 0, ??) ??(?,?) ?? ?? ?? 0 0 ?? 0 0 Qテーブル A B ???? ? |A, L 1 0 ???? ? |A, R 0 1 ???? ? |B , L 1 0 ???? ? |B, R 0 1
- 29. 課題2 41 ? 方策??4のステップ0の価値関数Vを以下の漸化式を用い て求め、方策??4について考察しなさい。 ? ??4 ?? ?? = 1、??4 ?? ?? = 1 A B ???? ? |A, L 1 0 ???? ? |A, R 0 1 ???? ? |B , L 1 0 ???? ? |B, R 0 1 状態：X ∈ A,B 行動：Y ∈ L, R ?? B L R RL 報酬関数：?? ??, ??, B = 1 それ以外は０ 状態遷移確率 割引率：γ = 0.9 次の状態 ステップ数：?? = 2 初期状態確率：???? A = 1 ????4 0 (??) = Ε ?? ??0|??0 ????(??1|??0,??0) ??? ??0, ??0, ??1 + ??????4 1 (??1) ??0 = ?? 時刻ステップ1の価値関数： 時刻ステップ0 ????4 1 ?? = 0.9 ????4 1 ?? = 1.9
- 30. 構成 43 ? 强化学习の基础の復習 ? データを用いた価値関数の最適化 ? 行動価値関数とQテーブル ? Q学習 ? Q学習の実装例 ? openAIを用いたQ学習の実装?実行例 ? その他 ? 方策オン型の方策反復法
- 31. OpenAI Gym (https://gym.openai.com/) 44 ? 強化学習のアルゴリズムを評価するための様々な ベンチマークツールが動作するプラットフォーム ? ベンチマークツールの例：Atariゲーム、古典制御、ロボット Atariゲーム：Pacman, Pongなど 古典制御：mountaincar, Acrobot, cartpoleなど ロボット：PickAndPlace, HandManiPulateBlockなど
- 32. WindowでのOpenAI Gymの利用方法 45 ? OpenAI Gymは基本的にLinux環境でしか動作しない ? ただし、Windows subsystem for Linuxを用いてwindowsに Ubuntuをインストールした環境でもOpen AI Gymは動作可 ? 必要な構成： ? Windows subsystem for Linux, Ubuntu ? Python3: Anaconda ? Xming: Xサーバ ? openAI Gym一式 ? 詳細は以下を参照： http://hirotaka-hachiya.hatenablog.com/entry/2018/05/28/185128
- 33. Pythonを用いたQ学習の実装例 46 ? 状態の離散化、行動の選択?実行の処理が必要 ? Qテーブルの更新は、単純な計算で数行で書ける ? 詳細は以下を参照： https://github.com/hhachiya/intelligentSystemTraining/blob/master/ mountainCar.py ? 学習時：「isdemo = False」にして、「python mountainCar.py」を実行 ? デモ時：「isdemo = True」にして、「python mountainCar.py」を実行 次の状態next_stateにおける最大 の価値を取得 現在の状態stateにおける価値を取得 Qテーブルの更新
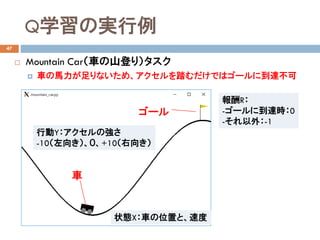
- 34. Q学習の実行例 47 ? Mountain Car（車の山登り）タスク ? 車の馬力が足りないため、アクセルを踏むだけではゴールに到達不可 状態X：車の位置と、速度 行動Y：アクセルの強さ -10（左向き）、０、+10（右向き） 車 ゴール 報酬R： -ゴールに到達時：0 -それ以外：-1
- 35. レポートの提出方法 48 ? 演習レポート： ? タイトル「演習レポート」、日付?学生番号?氏名を用紙の一番上に記載 ? 課題レポート ： ? タイトル「課題レポート」、出題日?学生番号?氏名を用紙の一番上に記載 ? 2ページ以上になる場合は、ホッチキス留め ? A4サイズの用紙を使用 ? 一度に複数の課題レポートを提出する場合出題日ごとに別々に綴じる
- 36. 構成 49 ? 强化学习の基础の復習 ? データを用いた価値関数の最適化 ? 行動価値関数とQテーブル ? Q学習 ? Q学習の実装例 ? openAIを用いたQ学習の実装?実行例 ? その他 ? 方策オン型の方策反復法
- 37. 方策反復法 50 ? Q関数の近似（方策評価）と、方策改善を繰り返す ? 方策評価：現在の方策 に対する価値関数 を計算 ? 方策改善：価値関数を用いて方策を更新 ? 最適な政策への収束が保証 ? どうやってQテーブルを近似する？ 方策評価 方策改善 価値関数 方策 初期政策 ：反復インデックス??1 ?????? (??, ??) ????+1 (??|??) ?? ????+1 ?? ?? = ? 1 0 if a = argmax ??? ?? ???? (??, ???) otherwise ??????+1 (??, ??) ≥ ?? ???? ??, ?? ?(??, ??) ?? ???? ????
- 38. モンテカルロ法による価値の近似 51 ? モンテカルロ法 ? 解析的に解けない問題をデータを用いて近似する方法の総称 ? カジノで有名なモナコのモンテカルロ地区が名前の由来 ? エピソードデータを用いて価値関数を近似的 ???? (??, ??) ≈ 1 ????(??,??) ? ??∈??(??,??) ? ??=??(??,??) ?? ?? ???????(??,??) ?? ????,?? ????(??,??)： ??(??, ??)の数 ??(??, ??)：状態??と行動??を含むエピソードの集合 ??(??,??) ?? ： エピソード??で(??, ??)が最初に現れるステップ
- 39. 価値関数近似と方策改善の例 52 ? エピソードデータを用いて価値関数を近似 ? 方策を改善 ???? (??, ??) ≈ 1 ????(??,??) ? ??∈??(??,??) ? ??=??(??,??) ?? ?? ???????(??,??) ?? ????,?? ?? ≡ ?? ?? ??=1 5 ??1 ≡ ??, ??, 0, ?? , (??, ??, 1, ??) ??2 ≡ ??, ??, 0, ?? , (??, ??, 0, ??) ??3 ≡ ??, ??, 1, ?? , (??, ??, 1, ??) ??4 ≡ ??, ??, 1, ?? , (??, ??, 0, ??) ??5 ≡ ??, ??, 0, ?? , (??, ??, 1, ??) エピソードデータ： 価値関数の近似式： ?? ??1 A, ?? ≈ 1 3 0 + 0.9 ? 1 + 0 + 0.9 ? 0 + 0 + 0.9 ? 1 = 0.6 ????1 A, ?? ≈ 1 4 1 + 1 + 0.9 ? 1 + 1 + 0.9 ? 0 + 1 = 1.225 ????1 ??, ?? ≈ 1 1 (0) = 0 ????1 ??, ?? ≈ 1 1 1 = 1 ????+1 ?? ?? = ? 1 0 if a = argmax ??? ?? ???? (??, ???) otherwise ??2 ?? ?? = 1 ??2 ?? ?? = 0 ??2 ?? ?? = 1 ??2 ?? ?? = 0