データ解析3 最适化の復习
- 1. データ解析 第3回 2018年4月26日 八谷 大岳 1
- 3. 内容:最適化手法の復習 9 ? 連立方程式の解法 ? 行列演算を用いた方法 ? 制約なしの最適化問題の解法 ? 微分を用いた方法 ? 偏微分を用いた方法 ? 行列、ベクトルの微分 ? 制約ありの最適化問題の解法 ? ラグランジュ未定乗数法
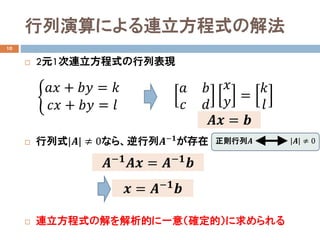
- 4. 行列演算による連立方程式の解法 10 ? 2元1次連立方程式の行列表現 ? 行列式|??| ≠ 0なら、逆行列????? が存在 ? 連立方程式の解を解析的に一意(確定的)に求められる ? ???? + ???? = ?? ???? + ???? = ?? ?? ?? ?? ?? ?? ?? = ?? ?? ???? = ?? ????? ???? = ????? ?? ?? = ????? ?? 正則行列?? |??| ≠ 0
- 5. 2次正方行列の逆行列 11 ? 行列式が0の場合:逆行列は無限に発散するため存在しない ? 逆行列の計算例: ? 逆行列が正しいか否かの確認 ?? ?? ?? ?? ?1 = 1 ????????? ?? ??? ??? ?? 行列式と等しい 3 2 5 1 ?1 = ? 1 7 1 ?2 ?5 3 ? 1 7 1 ?2 ?5 3 3 2 5 1 = ? 1 7 ?7 0 0 ?7 = 1 0 0 1 ?????1 = ??
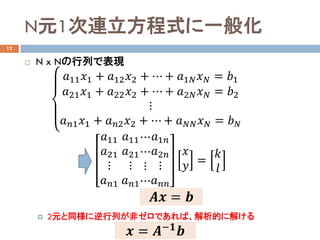
- 6. N元1次連立方程式に一般化 12 ? N x Nの行列で表現 ? 2元と同様に逆行列が非ゼロであれば、解析的に解ける ??11 ??1 + ??12 ??2 + ? + ??1?? ???? = ??1 ??21 ??1 + ??22 ??2 + ? + ??2?? ???? = ??2 ? ????1 ??1 + ????2 ??2 + ? + ?????? ???? = ???? ??11 ??21 ? ????? ??11 ??21 ? ????? ? ? ? ? ??1?? ??2?? ? ?????? ?? ?? = ?? ?? ???? = ?? ?? = ????? ??
- 7. 演習1 13 ? 以下の2元1次連立方程式の解が一意に求められるか確認 し、解を求めなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 ? 2?? ? 3?? = 5 4?? + ?? = ?2
- 8. 様々な連立方程式の行列表現 15 ? 1次形式(linear form)の行列表現 ? 双1次形式(bilinear form)の行列表現 ? 2次形式(quadratic form)の行列表現 ??11 ??12 ??21 ??22 ??1 ??2 = ??1 ??2 ???? = ?? ???? ???? = ?? ???? ???? = ????1 ??2 ??11 ??12 ??21 ??22 ??1 ??2 = ??1 ??2 ??1 ??2 ??11 ??12 ??21 ??22 ??1 ??2 = ??1 ??2
- 9. 内容:最適化手法の復習 16 ? 連立方程式の解法 ? 行列演算を用いた方法 ? 制約なしの最適化問題の解法 ? 微分を用いた方法 ? 偏微分を用いた方法 ? 行列、ベクトルの微分 ? 制約ありの最適化問題の解法 ? ラグランジュ未定乗数法
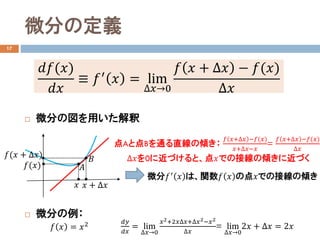
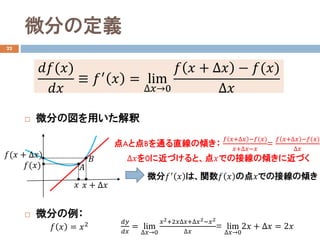
- 10. 微分の定義 17 ? 微分の図を用いた解釈 ? 微分の例: ????(??) ???? ≡ ??′ ?? = lim ???→0 ?? ?? + ??? ? ??(??) ??? ??(??) ?? ?? + ??? ??(?? + ???) 点Aと点Bを通る直線の傾き: ?? ??+??? ???(??) ??+?????? = ?? ??+??? ???(??) ??? ???を0に近づけると、点??での接線の傾きに近づく ?? ?? 微分??′ ?? は、関数?? ?? の点??での接線の傾き ?? ?? = ??2 ???? ???? = lim ???→0 ??2+2?????+???2???2 ??? = lim ???→0 2?? + ??? = 2??
- 11. 微分を用いた最適化 18 ? 関数の極値(極大、極小)の必要十分条件 ? 極大: ??′ ?? が正から負に反転 ? 極小: ??′ ?? が負から正に反転 ??′ ?? = 0 ?? ?? が極値 必要十分条件 ??の前後で??? ?? の符号が反転 極大 極小 最大 最小 ??′ ?? = 0だが、 ??′ ?? が 正から正で反転していない 微分が0だが 極値ではない
- 12. 演習2 19 ? 極大値と極小値を求めなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 ?? ?? = ??3 ? 12??2 + 36?? + 8
- 13. 内容:最適化手法の復習 21 ? 連立方程式の解法 ? 行列演算を用いた方法 ? 制約なしの最適化問題の解法 ? 微分を用いた方法 ? 偏微分を用いた方法 ? 行列、ベクトルの微分 ? 制約ありの最適化問題の解法 ? ラグランジュ未定乗数法
- 14. 微分の定義 22 ? 微分の図を用いた解釈 ? 微分の例: ????(??) ???? ≡ ??′ ?? = lim ???→0 ?? ?? + ??? ? ??(??) ??? ??(??) ?? ?? + ??? ??(?? + ???) 点Aと点Bを通る直線の傾き: ?? ??+??? ???(??) ??+?????? = ?? ??+??? ???(??) ??? ???を0に近づけると、点??での接線の傾きに近づく ?? ?? 微分??′ ?? は、関数?? ?? の点??での接線の傾き ?? ?? = ??2 ???? ???? = lim ???→0 ??2+2?????+???2???2 ??? = lim ???→0 2?? + ??? = 2??
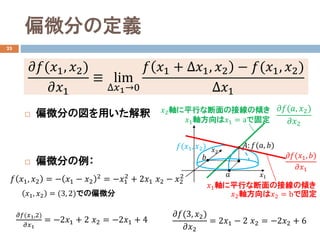
- 15. 偏微分の定義 23 ? 偏微分の図を用いた解釈 ? 偏微分の例: ????(??1, ??2) ????1 ≡ lim ???1→0 ?? ??1 + ???1, ??2 ? ??(??1, ??2) ???1 ?? ??1, ??2 = ? ??1 ? ??2 2 = ???1 2 + 2??1 ??2 ? ??2 2 ??1 ??2 ??: ??(??, ??) ?? ?? ????(??, ??2) ????2 ??2軸に平行な断面の接線の傾き ??1軸方向は??1 = aで固定 ????(??1, ??) ????1 ??1軸に平行な断面の接線の傾き ??2軸方向は??2 = bで固定 ????(??1,2) ????1 = ?2??1 + 2 ??2 = ?2??1 + 4 ??1, ??2 = (3, 2)での偏微分 ????(3, ??2) ????2 = 2??1 ? 2 ??2 = ?2??2 + 6 ??(??1, ??2)
- 16. 演習3 24 ? ?? ??, ?? の最小値と、最小解 ???, ??? を求めなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 ?? ??, ?? = ??2 + ??2 + 2?? + 4?? + 8
- 17. 内容:最適化手法の復習 26 ? 連立方程式の解法 ? 行列演算を用いた方法 ? 制約なしの最適化問題の解法 ? 微分を用いた方法 ? 偏微分を用いた方法 ? 行列、ベクトルの微分 ? 制約ありの最適化問題の解法 ? ラグランジュ未定乗数法
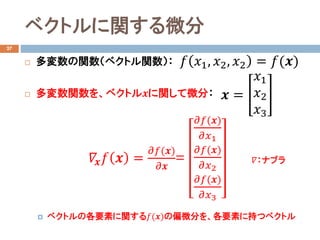
- 18. ベクトルに関する微分 27 ? 多変数の関数(ベクトル関数): ? 多変数関数を、ベクトル??に関して微分: ? ベクトルの各要素に関する??(??)の偏微分を、各要素に持つベクトル ?? ??1, ??2, ??2 = ??(??) ?? = ??1 ??2 ??3 ???? ?? ?? = ????(??) ???? = ????(??) ????1 ????(??) ????2 ????(??) ????3 ??:ナブラ
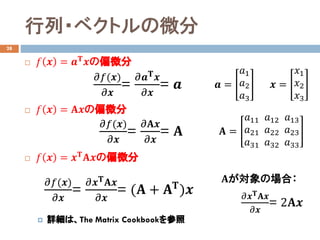
- 19. 行列?ベクトルの微分 28 ? ?? ?? = ???? ??の偏微分 ? ?? ?? = ????の偏微分 ? ?? ?? = ???? ????の偏微分 ? 詳細は、The Matrix Cookbookを参照 ?? = ??1 ??2 ??3 ????(??) ???? = ?????? ?? ???? = ?? ????(??) ???? = ?????? ???? = ?? ?? = ??11 ??21 ??31 ??12 ??22 ??32 ??13 ??23 ??33 ?? = ??1 ??2 ??3 ????(??) ???? = ?????? ???? ???? = (?? + ???? )?? ??が対象の場合: ?????? ???? ???? = 2????
- 20. 内容:最適化手法の復習 29 ? 連立方程式の解法 ? 行列演算を用いた方法 ? 制約なしの最適化問題の解法 ? 微分を用いた方法 ? 偏微分を用いた方法 ? 行列、ベクトルの微分 ? 制約ありの最適化問題の解法 ? ラグランジュ未定乗数法
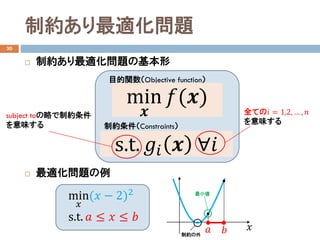
- 21. 制約あり最適化問題 30 ? 制約あり最適化問題の基本形 ? 最適化問題の例 目的関数(Objective function) min ?? ??(??) 制約条件(Constraints) s.t. ???? ?? ??? subject toの略で制約条件 を意味する 全ての?? = 1,2, … , ?? を意味する ???? ?? 最小値 min ?? (?? ? 2)2 s.t. ?? ≤ ?? ≤ ?? 制約の外
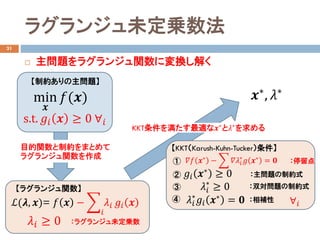
- 22. ? 主問題をラグランジュ関数に変換し解く ラグランジュ未定乗数法 31 【制約ありの主問題】 min ?? ??(??) s.t. ???? ?? ≥ 0 ??? 【ラグランジュ関数】 ?(??, ??)= ?? ?? ? ? ?? ???? ???? ?? ???? ≥ 0 :ラグランジュ未定乗数 目的関数と制約をまとめて ラグランジュ関数を作成 KKT条件を満たす最適な??? と??? を求める 【KKT(Karush-Kuhn-Tucker)条件】 ① ② ③ ④ :停留点 :主問題の制約式 :双対問題の制約式 :相補性 ???? ??? ? ? ?????? ? ?? ??? = ?? ???? ??? ≥ 0 ???? ? ≥ 0 ???? ? ???? ??? = ?? ??? , ??? ???
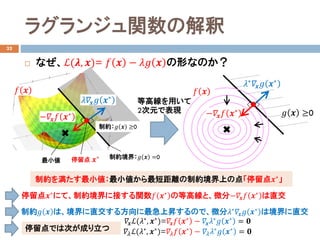
- 23. ラグランジュ関数の解釈 32 ? なぜ、?(??, ??)= ?? ?? ? ???? ?? の形なのか? ?? ?? 最小値 等高線を用いて 2次元で表現 ?????? ?? ??? 制約:?? ?? ≥0 制約境界:?? ?? =0 ????? ?? ??? 停留点 停留点???にて、制約境界に接する関数?? ??? の等高線と、微分????? ?? ??? は直交 制約?? ?? は、境界に直交する方向に最急上昇するので、微分??? ???? ?? ??? は境界に直交 停留点では次が成り立つ ??? ?????(???, ???)=???? ?? ??? ? ???? ??? ?? ??? = ?? ?????(???, ???)=???? ?? ??? ? ???? ??? ?? ??? = ?? ?? ?? ≥0????? ?? ??? ?? ?? ??? ???? ?? ??? 制約を満たす最小値:最小値から最短距離の制約境界上の点「停留点??? 」
- 24. ラグランジュ未定乗数法の例 33 ? ラグランジュ関数を求める ? 偏微分して0と置く min ??,??,?? ??2 + ??2 + ??2 s.t. ?? + ?? + ?? = 1 ?(??, ??, ??, ??)=??2 + ??2 + ??2 ? ??(?? + ?? + ?? ? 1) ?? ≥ 0 ??? ???? = 2?? ? ?? = 0 ??? ???? = 2?? ? ?? = 0 主問題: ??? ???? = 2?? ? ?? = 0 ??? ? ?? ? ?? + 1= ? 3 2 ?? + 1 = 0 ??? ???? = ??? ? ?? ? ?? + 1=0 ?? = ?? = ?? = 1 2 ?? ∴ ??? = 2 3 ∴ ??? = ??? = ??? = 1 3
- 25. 演習4 34 ? 最適解???と???を求めなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 min ??,?? ??2 + ??2 s.t. ?? + ?? = 1 主問題:
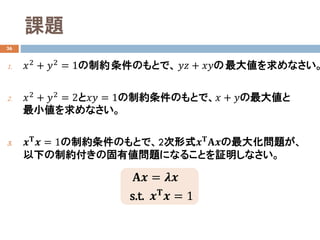
- 26. 課題 36 1. ??2 + ??2 = 1の制約条件のもとで、 ???? + ????の最大値を求めなさい。 2. ??2 + ??2 = 2と???? = 1の制約条件のもとで、?? + ??の最大値と 最小値を求めなさい。 3. ???? ?? = 1の制約条件のもとで、2次形式???? ????の最大化問題が、 以下の制約付きの固有値問題になることを証明しなさい。 ???? = ???? s.t. ???? ?? = 1
- 27. レポートの提出方法 37 ? 演習レポート: ? タイトル「演習レポート」、日付?学生番号?氏名を用紙の一番上に記載 ? 課題レポート : ? タイトル「課題レポート」、出題日?学生番号?氏名を用紙の一番上に記載 ? 2ページ以上になる場合は、ホッチキス留め ? A4サイズの用紙を使用 ? 一度に複数の課題レポートを提出する場合出題日ごとに別々に綴じる