データ解析7 主成分分析の基础
- 1. データ解析 第7回 2018年5月31日 八谷 大岳 1
- 3. 内容: 6 ? 主成分分析の基础 ? 主成分分析とは ? 主成分分析の定式化 ? 分散最大化問題への変形 ? 主成分分析の計算 ? ラグランジュ未定乗数法を用いた主成分軸の導出 ? 主成分軸の計算手順
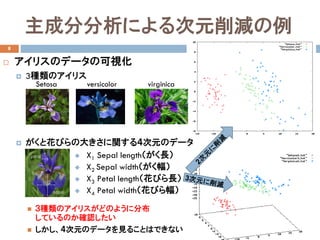
- 4. 主成分分析 7 ? 主成分分析:代表的かつ基本的な次元削減手法 ? 英語では、Principal Component Analysis (PCA) ? 次元削減:データの次元を、人間が目視可能な2次元または 3次元に削減すること ? 3次元から2次元に削減する例:データを表す2次元平面を探す ??1 ??2 3次元空間上に分布するデータ がある平面の上に乗っている 平面の2次元空間上でデータ を表現可能 ??1 ??3靴のサイズ
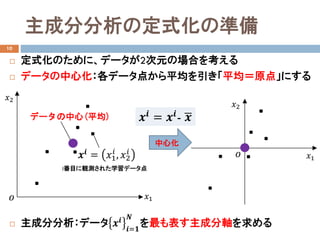
- 5. 主成分分析による次元削減の例 8 ? アイリスのデータの可視化 ? 3種類のアイリス ? がくと花びらの大きさに関する4次元のデータ ? 3種類のアイリスがどのように分布 しているのか確認したい ? しかし、4次元のデータを見ることはできない ? X1 Sepal length(がく長) ? X2 Sepal width(がく幅) ? X3 Petal length(花びら長) ? X4 Petal width(花びら幅) Setosa versicolor virginica
- 6. 内容: 9 ? 主成分分析の基础 ? 主成分分析とは ? 主成分分析の定式化 ? 分散最大化問題への変形 ? 主成分分析の計算 ? 主成分軸の導出 ? 主成分軸の計算手順
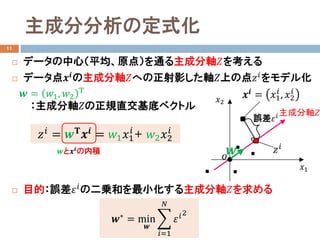
- 7. 主成分分析の定式化の準備 10 ? 定式化のために、データが2次元の場合を考える ? データの中心化:各データ点から平均を引き「平均=原点」にする ? 主成分分析:データ ???? ??=?? ?? を最も表す主成分軸を求める ??2 ?? i番目に観測された学習データ点 ???? = ??1 ?? , ??2 ?? ??1 ?? ??1 ??2 中心化 ???? = ????- ???データの中心(平均)
- 8. 主成分分析の定式化 11 ? データの中心(平均、原点)を通る主成分軸??を考える ? データ点????の主成分軸??への正射影した軸??上の点????をモデル化 ? 目的:誤差????の二乗和を最小化する主成分軸??を求める ??? = min ?? ? ??=1 ?? ????2 ???? = ???? ???? = ??1 ??1 ?? + ??2 ??2 ?? ?? = ??1, ??2 Τ :主成分軸??の正規直交基底ベクトル 主成分軸?? ??1 ??2 ?? ???? = ??1 ?? , ??2 ?? 誤差???? ???? ????と????の内積
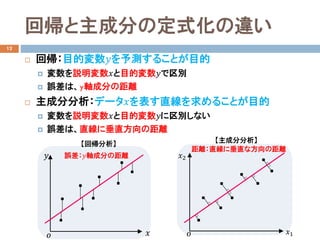
- 9. 回帰と主成分の定式化の違い 12 ? 回帰:目的変数??を予測することが目的 ? 変数を説明変数??と目的変数??で区別 ? 誤差は、y軸成分の距離 ? 主成分分析:データ??を表す直線を求めることが目的 ? 変数を説明変数??と目的変数??に区別しない ? 誤差は、直線に垂直方向の距離 誤差:??軸成分の距離 ?? ?? ?? 【回帰分析】 距離:直線に垂直な方向の距離 ?? 【主成分分析】 ??1 ??2
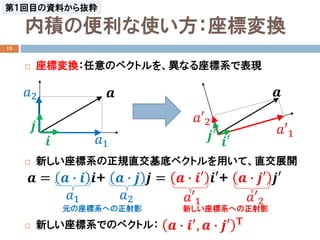
- 10. 内積の便利な使い方:座標変換 13 ? 座標変換:任意のベクトルを、異なる座標系で表現 ? 新しい座標系の正規直交基底ベクトルを用いて、直交展開 ? 新しい座標系でのベクトル: ??1 ?? ?? ?? ?? ?????? ?? = ?? ? ?? ??+ ?? ? ?? ?? = ?? ? ??? ???+ ?? ? ??? ??? ??2 ???1 ???2 ??1 ??2 元の座標系への正射影 ???1 ???2 新しい座標系への正射影 ?? ? ??′ , ?? ? ??? ?? 第1回目の資料から抜粋
- 11. 演習1 14 ? 主成分軸??と軸??1のなす角を??として、主成分軸上の点???? を、??を用いて表しなさい。 ? ヒント: ? 正規直交基底ベクトル??を求めて、????を正射影 ? 回転行列: ???????? ????????? ???????? ???????? ? 軸??1の正規直交基底ベクトル: ?? = 1 0 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の一番上 に記載 ??1 ??2 主成分の 候補?? ?? ?? ?? ?? ???? ???? ???? = ???? ???? = ??1 ??1 ?? + ??2 ??2 ??
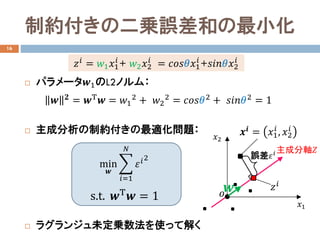
- 12. 制約付きの二乗誤差和の最小化 16 ? パラメータ??1のL2ノルム: ? 主成分析の制約付きの最適化問題: ? ラグランジュ未定乗数法を使って解く ?? ?? = ??Τ ?? = ??1 2 + ??2 2 = ????????2 + ????????2 = 1 ???? = ??1 ??1 ?? + ??2 ??2 ?? = ??????????1 ?? +??????????2 ?? min ?? ? ??=1 ?? ????2 s.t. ??Τ ?? = 1 主成分軸?? ??1 ??2 ?? ???? = ??1 ?? , ??2 ?? 誤差???? ???? ??
- 13. 内容: 17 ? 主成分分析の基础 ? 主成分分析とは ? 主成分分析の定式化 ? 分散最大化問題への変形 ? 主成分分析の計算 ? 主成分軸の導出 ? 主成分軸の計算手順
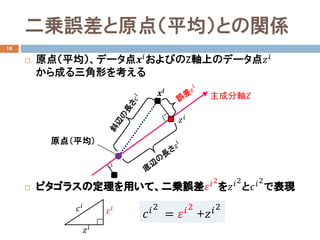
- 14. 二乗誤差と原点(平均)との関係 18 ? 原点(平均)、データ点????およびのZ軸上のデータ点???? から成る三角形を考える ? ピタゴラスの定理を用いて、二乗誤差????2 を????2 と????2 で表現 原点(平均) 主成分軸?????? ???? ???? ???? ???? ????2 = ????2 +????2
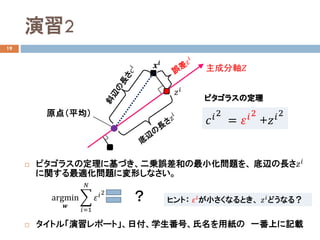
- 15. 演習2 19 ? ピタゴラスの定理に基づき、二乗誤差和の最小化問題を、 底辺の長さ???? に関する最適化問題に変形しなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上に記載 argmin ?? ? ??=1 ?? ????2 ? 原点(平均) 主成分軸?????? ???? ????2 = ????2 +????2 ピタゴラスの定理 ヒント: ????が小さくなるとき、 ????どうなる?
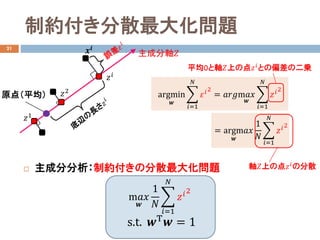
- 16. = argm???? ?? 1 ?? ? ??=1 ?? ????2 制約付き分散最大化問題 21 ? 主成分分析:制約付きの分散最大化問題 argmin ?? ? ??=1 ?? ????2 = ??????m???? ?? ? ??=1 ?? ????2 平均0と軸??上の点????との偏差の二乗 軸??上の点???? の分散 m???? ?? 1 ?? ? ??=1 ?? ????2 s.t. ??Τ ?? = 1 原点(平均) 主成分軸?????? ???? ??2 ??1
- 17. 内容: 22 ? 主成分分析の基础 ? 主成分分析とは ? 主成分分析の定式化 ? 分散最大化問題への変形 ? 主成分分析の計算 ? 主成分軸の導出 ? 主成分軸の計算手順
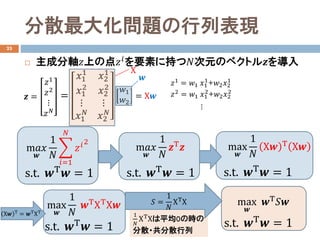
- 18. 分散最大化問題の行列表現 23 ? 主成分軸??上の点????を要素に持つ??次元のベクトル??を導入 m???? ?? 1 ?? ? ??=1 ?? ????2 s.t. ??Τ ?? = 1 = ??1 1 ??1 2 ? ??1 ?? ??2 1 ??2 2 ? ??2 ?? ??1 ??2 = X?? X ?? m???? ?? 1 ?? ??Τ ?? s.t. ??Τ ?? = 1 max ?? 1 ?? X?? Τ X?? s.t. ??Τ ?? = 1 max ?? 1 ?? ??ΤXΤX?? s.t. ??Τ ?? = 1 1 ?? XΤ Xは平均0の時の 分散?共分散行列 max ?? ??Τ ???? s.t. ??Τ ?? = 1 ?? = 1 ?? XΤ X ?? = ??1 ??2 ? ?? ?? ??1 = ??1 ??1 1 +??2 ??2 1 ??2 = ??1 ??1 2 +??2 ??2 2 ? X?? Τ = ??Τ XΤ
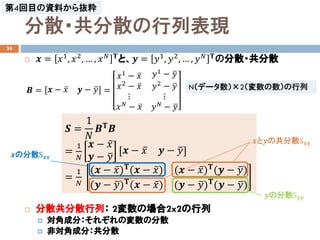
- 19. 分散?共分散の行列表現 24 ? ?? = ??1 , ??2 , … , ?? ?? ?? と、?? = ??1 , ??2 , … , ?? ?? ?? の分散?共分散 ? 分散共分散行列: 2変数の場合2x2の行列 ? 対角成分:それぞれの変数の分散 ? 非対角成分:共分散 ?? = 1 ?? ???? ?? = 1 ?? ?? ? ??? ?? ? ??? ?? ? ??? ?? ? ??? = 1 ?? (?? ? ???)??(?? ? ???) (?? ? ???)??(?? ? ???) (?? ? ???)?? (?? ? ???) (?? ? ???)?? (?? ? ???) ?? = ?? ? ??? ?? ? ??? = ??1 ? ??? ??2 ? ??? ? ?? ?? ? ??? ??1 ? ??? ??2 ? ??? ? ?? ?? ? ??? ??の分散S???? ??の分散S???? ??と??の共分散S???? N(データ数)×2(変数の数)の行列 第4回目の資料から抜粋
- 20. 演習3 25 1. 制約付き分散最大化問題のラグランジュ関数を書きなさい。 2. ラグランジュ関数を偏微分して0と置き最適解の式を求めなさい。 ? タイトル「演習レポート」、日付、学生番号、氏名を用紙の 一番上 に記載 max ?? ??Τ ???? s.t. ??Τ ?? = 1
- 21. 内容: 27 ? 主成分分析の基础 ? 主成分分析とは ? 主成分分析の定式化 ? 分散最大化問題への変形 ? 主成分分析の計算 ? 主成分軸の導出 ? 主成分軸の計算手順
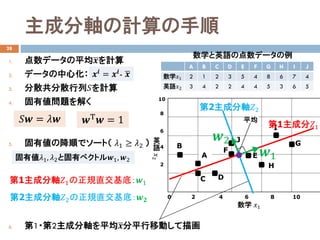
- 22. 主成分軸の計算の手順 28 1. 点数データの平均???を計算 2. データの中心化: 3. 分散共分散行列??を計算 4. 固有値問題を解く 5. 固有値の降順でソート( ??1 ≥ ??2 ) 6. 第1?第2主成分軸を平均???分平行移動して描画 A B C D E F G H I J 数学??1 2 1 2 3 5 4 8 6 7 4 英語??2 3 4 2 2 4 4 5 3 6 5 ???? = ????- ??? 第1主成分軸??1の正規直交基底:??1 数学と英語の点数データの例 ???? = ???? ??Τ ?? = 1 固有値??1, ??2と固有ベクトル??1, ??2 第2主成分軸??2の正規直交基底:???? 英 語 A B C D E F H GJ I 0 2 4 6 8 10 10 8 6 4 2 数学 ??1 第2主成分軸??2 ??2 第1主成分??1 ??1 平均
- 23. 課題 29 ? 英語と数学の点数データに対する主成分分析 1. データの中心化をしなさい。 2. 中心化した点数データの分散共分散行列??を求めなさい。 3. 行列??の固有値問題を解き、固有値と固有ベクトルを 求めなさい。 4. 第1?第2主成分軸の式を求めなさい。 5. 点数データと、第1?第2主成分軸をグラフに描きなさい。 A B C D E 数学??1 50 70 65 60 75 英語??2 85 75 80 70 90 数学と英語の点数データの例
- 24. レポートの提出方法 30 ? 演習レポート: ? タイトル「演習レポート」、日付?学生番号?氏名を用紙の一番上に記載 ? 課題レポート : ? タイトル「課題レポート」、出題日?学生番号?氏名を用紙の一番上に記載 ? 2ページ以上になる場合は、ホッチキス留め ? A4サイズの用紙を使用 ? 一度に複数の課題レポートを提出する場合出題日ごとに別々に綴じる