20200605 oki lecture4
- 1. 2020年度 建築計画第二 (第10回 2020.06.05) 建築?都市における 相関?因果関係の分析手法 2 東京工業大学 環境?社会理工学院 建築学系 沖 拓弥 12020年度 建築計画第二 第10回(沖 拓弥)
- 2. 2 第9回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 相関分析 と 回帰分析 相関分析(Correlation analysis) 2種類の変数XY間の因果関係を考えずに,変数 間の関係の強さを測定する方法。 回帰分析(Regression analysis) 2種類の変数XY間の因果関係を仮定し,変数X が変数Yに与える影響の測定や,予測に用いら れる方法。
- 3. 3 第9回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 相関分析 と 回帰分析 相関分析(Correlation analysis) 2種類の変数XY間の因果関係を考えずに,変数 間の関係の強さを測定する方法。 回帰分析(Regression analysis) 2種類の変数XY間の因果関係を仮定し,変数X が変数Yに与える影響の測定や,予測に用いら れる方法。 変数間の関係を1対1で考え,回帰式を推定した ?実際は様々な要因が複合して関係する場合が多い ?精度高く予測するためには,複数の要因を説明変数 とした「重回帰式」を推定する必要がある。
- 4. 4 第9回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 相関分析 と 回帰分析 相関分析(Correlation analysis) 2種類の変数XY間の因果関係を考えずに,変数 間の関係の強さを測定する方法。 回帰分析(Regression analysis) 2種類の変数XY間の因果関係を仮定し,変数X が変数Yに与える影響の測定や,予測に用いら れる方法。 変数間の関係を1対1で考え,回帰式を推定した ?実際は様々な要因が複合して関係する場合が多い ?精度高く予測するためには,複数の要因を説明変数 とした「重回帰式」を推定する必要がある。
- 5. 5 例えば??? 2020年度 建築計画第二 第10回(沖 拓弥) 賃貸住宅の賃料にはどのような要因が関係するだろう? ? 最寄り駅 ? 最寄り駅からの徒歩時間 ? 間取りタイプ ? 築後年数 ? 専有面積 ? バス?トイレ別かどうか ? 2階以上かどうか ? オートロックかどうか ? 構造 ? 採光(向き/面数) ?????? それぞれ賃料に影響していそうだが,ひとつの要因で決まるわけ ではない。また,影響度合いも要因によって異なる。
- 6. 6 第9回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 相関分析 と 回帰分析 相関分析(Correlation analysis) 2種類の変数XY間の因果関係を考えずに,変数 間の関係の強さを測定する方法。 回帰分析(Regression analysis) 2種類の変数XY間の因果関係を仮定し,変数X が変数Yに与える影響の測定や,予測に用いら れる方法。 変数間の関係を1対1で考え,回帰式を推定した ?実際は様々な要因が複合して関係する場合が多い ?精度高く予測するためには,複数の要因を説明変数 とした「重回帰式」を推定する必要がある。
- 7. 7 第10回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 重回帰分析 と 数量化理論Ⅰ類 重回帰分析(Multiple regression analysis) 複数の説明変数X(定量的データ)が目的変数Yに与 える影響の測定や,予測に用いられる方法。 数量化理論Ⅰ類(Hayashi’s quantification theory I) 複数の要因X(定性的データ)が外的基準Yに与える 影響の測定や,予測に用いられる方法。 *定性的データ:名義尺度,順序尺度など Yes/No,ランク
- 8. 8 第10回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 重回帰分析 と 数量化理論Ⅰ類 重回帰分析(Multiple regression analysis) 複数の説明変数X(定量的データ)が目的変数Yに与 える影響の測定や,予測に用いられる方法。 数量化理論Ⅰ類(Hayashi’s quantification theory I) 複数の要因X(定性的データ)が外的基準Yに与える 影響の測定や,予測に用いられる方法。 *定性的データ:名義尺度,順序尺度など Yes/No,ランク
- 9. 9 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 重回帰式は,一般に以下のような形で表される。 0 1 1 2 2 p py x x xβ β β β= + + + +? y:目的変数 x1, x2, ???, xp:説明変数 β0, β1, β2, ???, βp:回帰係数 ※偏回帰係数,重回帰係数とも。 単回帰分析(第9回)の場合と同様にして, 回帰係数 βi の求め方を考えよう。
- 10. 10 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 次のようなn個の観測データが得られていたとする。 y x1 x2 x3 ??? xp 1 y1 x11 x21 x31 ??? xp1 2 y2 x12 x22 x32 ??? xp2 3 y3 x13 x23 x33 ??? xp3 : : : : : : n yn x1n x2n x3n ??? xpn yとx1, x2, ???, xpとの間の関係を定式化すると, 0 1 1 2 2i i i p pi iy x x xβ β β β ε= + + + + +? 誤差項 or 確率的攪乱項
- 11. 11 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 0 1 1 2 2i i i p pi iy x x xβ β β β ε= + + + + +? 誤差自乗和が最小となるときの回帰係数を採用する。 ( ){ } 2 2 0 1 1 2 2 1 1 n n i i i i p pi i i S y x x xε β β β β = = = = ? + + + +∑ ∑ ? ( ){ }0 1 1 2 2 10 2 0 n i i i p pi i S y x x xβ β β β β = ? =? ? + + + + = ? ∑ ? ( ){ }1 0 1 1 2 2 11 2 0 n i i i i p pi i S x y x x xβ β β β β = ? =? ? + + + + = ? ∑ ? ( ){ }2 0 1 1 2 2 12 2 0 n i i i i p pi i S x y x x xβ β β β β = ? =? ? + + + + = ? ∑ ? ???
- 12. 12 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 整理すると, 0 1 1 2 2 1 1 1 1 n n n n i i i p pi i i i i y n x x xβ β β β = = = = = + + + +∑ ∑ ∑ ∑? 1 0 1 1 1 1 2 1 2 1 1 1 1 1 1 n n n n n i i i i i i i p i pi i i i i i x y x x x x x x xβ β β β = = = = = = + + + +∑ ∑ ∑ ∑ ∑? ??? 2 0 2 1 2 1 2 2 2 2 1 1 1 1 1 n n n n n i i i i i i i p i pi i i i i i x y x x x x x x xβ β β β = = = = = = + + + +∑ ∑ ∑ ∑ ∑? 0 1 1 2 2 1 1 1 1 1 n n n n n pi i pi pi i pi i p pi pi i i i i i x y x x x x x x xβ β β β = = = = = = + + + +∑ ∑ ∑ ∑ ∑? ???① ???②
- 13. 13 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) ①について, 0 1 1 2 2 1 1 1 1 n n n n i i i p pi i i i i y n x x xβ β β β = = = = = + + + +∑ ∑ ∑ ∑? 1 2 0 1 2 1 1 1 1 1 n n n n p i i i pi i i i i y x x x n n n n ββ β β = = = = ? ? = ? + + +? ? ? ? ∑ ∑ ∑ ∑? 整理して両辺nで割ると, つまり, ( )0 1 1 2 2 p py x x xβ β β β= ? + + +? 1 1 1 1n n i k ki i i y y x x n n= = = =∑ ∑ただし, である(平均値)。 ???①’
- 14. 14 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) ②について, 0 1 1 2 2 1 1 1 1 1 n n n n n pi i pi pi i pi i p pi pi i i i i i x y x x x x x x xβ β β β = = = = = = + + + +∑ ∑ ∑ ∑ ∑? ここで,①’を代入すると, ( ){ }1 1 2 2 1 n pi i p p p i x y y x x x nxβ β β = = ? + + +∑ ? 1 1 2 2 1 1 1 n n n pi i pi i p pi pi i i i x x x x x xβ β β = = = + + + +∑ ∑ ∑? 整理すると, 1 n p pi pi p p p i x x x x n β β = + + ?∑? 1 2 1 1 1 2 2 2 1 1 1 1 n n n pi i p pi i p pi i p i i i x y x y x x x x x x x x n n n β β β β = = ?= ? + ?∑ ∑ ∑
- 15. 15 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) ここで,共分散の定義が, 1 1 n p pi pi p p i x x x x n β = ? ? + + ?? ? ? ? ∑? 1 1 1 2 2 2 1 1 1 1 1 1n n n pi i p pi i p pi i p i i i x y x y x x x x x x x x n n n β β = = ? ? ? ? ?= ? + ?? ? ? ? ? ? ? ? ∑ ∑ ∑ (つづき) ( )( ) 1 1 1 1 1 1n n n n xy i i i i i i i i i i x x y y x y y x x y nxy n n σ = = = = ? ? = ? ?= ? ? +? ? ? ? ∑ ∑ ∑ ∑ 1 1 1 1n n i i i i i i x y xy xy xy x y xy n n= = ? ? += ?∑ ∑ と変形できることに着目すると,
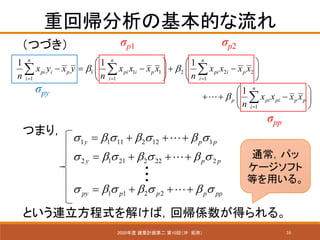
- 16. 16 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) (つづき) 1 1 n p pi pi p p i x x x x n β = ? ? + + ?? ? ? ? ∑? 1 1 1 2 2 2 1 1 1 1 1 1n n n pi i p pi i p pi i p i i i x y x y x x x x x x x x n n n β β = = ? ? ? ? ?= ? + ?? ? ? ? ? ? ? ? ∑ ∑ ∑ σpy σp1 σp2 σpp つまり, 1 1 11 2 12 1 2 1 21 2 22 2 y p p y p p σ β σ β σ β σ σ β σ β σ β σ = + + + = + + + ? ? 1 1 2 2py p p p ppσ β σ β σ β σ= + + +? ??? という連立方程式を解けば,回帰係数が得られる。 通常,パッ ケージソフト 等を用いる。
- 17. 17 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 1 1 11 2 12 1 2 1 21 2 22 2 y p p y p p σ β σ β σ β σ σ β σ β σ β σ = + + + = + + + ? ? 1 1 2 2py p p p ppσ β σ β σ β σ= + + +? ??? という連立方程式を解けば,回帰係数が得られる。 (つづき) 1 11 12 1 1 2 21 22 2 2 1 2 y p y p py p p pp p σ σ σ σ β σ σ σ σ β σ σ σ σ β ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?= ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???? = ????
- 18. 18 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) (つづき) ?? = ???1 ???? 連立方程式???? = ????が1組しか解を持たないことは, ??が正則であること,すなわち,逆行列??-1が存在する こと(行列式|??|≠0)と同値である。 逆行列??-1が存在するとき,
- 19. 19 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定した回帰係数を用いることで,最終的に 0 1 1 2 2 ? ? ? ??i i i p piy x x xβ β β β= + + + +? という重回帰式が得られる。
- 20. 20 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定結果の解釈 ①モデルの選択 ②残差分析 ③重相関係数R(自由度調整済み決定係数R2) ④回帰係数の値と符号 ⑤標準化回帰係数 ⑥多重共線性の発生有無の確認 ⑦説明変数の有意性の検証(t値,P値)
- 21. 21 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定結果の解釈 ①モデルの選択 ②残差分析 ③重相関係数R(自由度調整済み決定係数R2) ④回帰係数の値と符号 ⑤標準化回帰係数 ⑥多重共線性の発生有無の確認 ⑦説明変数の有意性の検証(t値,P値)
- 22. 22 説明変数が多いほど良いか? 2020年度 建築計画第二 第10回(沖 拓弥) ? 重回帰モデルの説明変数の数や次数を増やせば増やす ほど,データとの適合度を高めることができる(重相関係 数Rや自由度調整済決定係数R2の値も上昇する)。 ? しかし,その反面,ノイズなどの偶発的な変動にも無理矢 理合わせてしまうため,同種のデータには合わなくなる (過適合:Overfitting)。 ? そこで,モデルの複雑さと,データの適合度(当てはまり 具合)とのバランスを取るために,AIC(赤池情報量規準) がよく使用される。 ? AICの値が最小となるモデルを選択すれば,多くの場合, 良いモデルが選択できる。
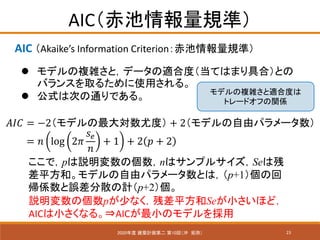
- 23. 23 AIC(赤池情報量規準) 2020年度 建築計画第二 第10回(沖 拓弥) AIC (Akaike’s Information Criterion:赤池情報量規準) ? モデルの複雑さと,データの適合度(当てはまり具合)との バランスを取るために使用される。 ? 公式は次の通りである。 ???? ?? = ?2(モデルの最大対数尤度) + 2(モデルの自由パラメータ数) ???? ?? = ?? log 2?? ???? ?? + 1 + 2 ?? + 2 ここで,pは説明変数の個数,nはサンプルサイズ,Seは残 差平方和。モデルの自由パラメータ数とは,(p+1)個の回 帰係数と誤差分散の計(p+2)個。 説明変数の個数pが少なく,残差平方和Seが小さいほど, AICは小さくなる。?AICが最小のモデルを採用 モデルの複雑さと適合度は トレードオフの関係
- 24. 24 AICの考え方を整理 2020年度 建築計画第二 第10回(沖 拓弥) AIC=-2(モデルの最大対数尤度)+2(モデルの自由パラ メータ数) ? モデルの良さは,データから構築したモデルが将来の現象 予測にどの程度有効に機能するか,という観点から捉える 必要がある。 ? 観測データに対して当てはまりの良いモデルを求めるには, 多数のパラメータを含む複雑なモデルの方が良いが,複雑 すぎるモデルは将来の現象予測に有効に働かない。 ? 予測の観点から最適なモデルを選択するには,モデルの データへの適合度とモデルの複雑さを適切に制御する必 要がある。 ? AICは,観測データへのモデルの当てはまりの良さを最大 対数尤度で測り,自由パラメータ数がモデルの複雑さに対 するペナルティとして機能している。
- 25. 25 モデルの選択について 2020年度 建築計画第二 第10回(沖 拓弥) ? 説明変数の候補がN個あるとすると,単純な線形重 回帰であっても2N通りのモデルが考えられる。 ?効率の良いモデル選択方法が必要。 ? ステップワイズ(stepwise)法を用いて,1つずつ説明 変数を追加したり,削除したりしながら,最適な説明 変数の組み合わせを探すことが多い。 ? ステップワイズ法にも,変数増加法,変数減少法,変 数増減法,変数増減法の4通りがある。
- 26. 26 ステップワイズ(stepwise)法の種類 2020年度 建築計画第二 第10回(沖 拓弥) https://datachemeng.com/stepwise/
- 27. 27 どのように説明変数を増やすか? 2020年度 建築計画第二 第10回(沖 拓弥) https://datachemeng.com/stepwise/ AIC
- 28. 28 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定結果の解釈 ①モデルの選択 ②残差分析 ③重相関係数R(自由度調整済み決定係数R2) ④回帰係数の値と符号 ⑤標準化回帰係数 ⑥多重共線性の発生有無の確認 ⑦説明変数の有意性の検証(t値,P値)
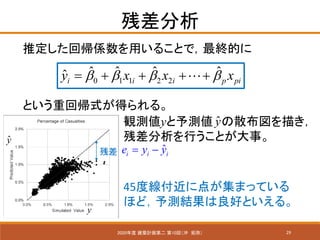
- 29. 29 残差分析 2020年度 建築計画第二 第10回(沖 拓弥) 推定した回帰係数を用いることで,最終的に 0 1 1 2 2 ? ? ? ??i i i p piy x x xβ β β β= + + + +? という重回帰式が得られる。 y ?y 残差 ?i i ie y y= ? 観測値yと予測値 の散布図を描き, 残差分析を行うことが大事。 ?y 45度線付近に点が集まっている ほど,予測結果は良好といえる。
- 30. 30 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定結果の解釈 ①モデルの選択 ②残差分析 ③重相関係数R(自由度調整済み決定係数R2) ④回帰係数の値と符号 ⑤標準化回帰係数 ⑥多重共線性の発生有無の確認 ⑦説明変数の有意性の検証(t値,P値)
- 31. 31 重相関係数と自由度調整済み決定係数 2020年度 建築計画第二 第10回(沖 拓弥) 重相関係数 自由度調整済み決定係数 実際に観測された目的変数(被説明変数)の値と, 重回帰式をあてはめて計算した推定値(理論値)との 相関係数(0≤R≤1)。 AICと同じく,重相関係数もモデルが複雑になるほど 大きくなるため,その影響を考慮した決定係数。
- 32. 32 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定結果の解釈 ①モデルの選択 ②残差分析 ③重相関係数R(自由度調整済み決定係数R2) ④回帰係数の値と符号 ⑤標準化回帰係数 ⑥多重共線性の発生有無の確認 ⑦説明変数の有意性の検証(t値,P値)
- 33. 33 回帰係数の値?符号と標準化回帰係数 2020年度 建築計画第二 第10回(沖 拓弥) ? (偏)回帰係数は,相関分析での回帰直線の傾き と同じく,その説明変数xiと目的変数yとの間に正 負どちらの相関があるか,および,xiを1単位変化 させることがyをどの程度影響を与えるかを表す。 ? 一方,標準化(偏)回帰係数は,説明変数と目的 変数をそれぞれ(平均0,標準偏差1に)標準化した 上で得られる回帰係数で,オーダーの異なる説明 変数間の重要度を比較できる。符号は標準化前と 変わらない。 ?????? ? ????? ??????
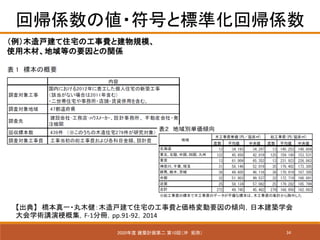
- 34. 34 回帰係数の値?符号と標準化回帰係数 2020年度 建築計画第二 第10回(沖 拓弥) 【出典】 橋本真一?丸木健:木造戸建て住宅の工事費と価格変動要因の傾向,日本建築学会 大会学術講演梗概集,F-1分冊,pp.91-92,2014 (例)木造戸建て住宅の工事費と建物規模、 使用木材、地域等の要因との関係
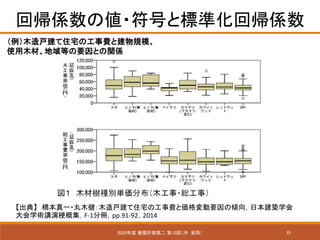
- 35. 35 回帰係数の値?符号と標準化回帰係数 2020年度 建築計画第二 第10回(沖 拓弥) 【出典】 橋本真一?丸木健:木造戸建て住宅の工事費と価格変動要因の傾向,日本建築学会 大会学術講演梗概集,F-1分冊,pp.91-92,2014 (例)木造戸建て住宅の工事費と建物規模、 使用木材、地域等の要因との関係
- 36. 36 回帰係数の値?符号と標準化回帰係数 2020年度 建築計画第二 第10回(沖 拓弥) 【出典】 橋本真一?丸木健:木造戸建て住宅の工事費と価格変動要因の傾向,日本建築学会 大会学術講演梗概集,F-1分冊,pp.91-92,2014 (例)木造戸建て住宅の工事費と建物規模、 使用木材、地域等の要因との関係
- 37. 37 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定結果の解釈 ①モデルの選択 ②残差分析 ③重相関係数R(自由度調整済み決定係数R2) ④回帰係数の値と符号 ⑤標準化回帰係数 ⑥多重共線性の発生有無の確認 ⑦説明変数の有意性の検証(t値,P値)
- 38. 38 多重共線性の問題について 2020年度 建築計画第二 第10回(沖 拓弥) 多重共線性(Multicollinearity,マルチコ) 説明変数のうちのいくつかが,相互に関連しており,そ のために単独の影響を分離したり,効果を評価したりす ることが,不可能ではないにしても,困難な状態。 (Goldberger, 1968) ?? = ???1 ???? ??が正則でない,つまり,逆行列??-1が存在しないとき, のβ の解は不安定となり求めることができない。 (回帰係数の正負が矛盾するなどの問題が生じる)
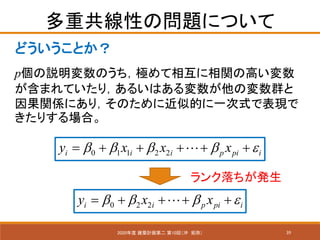
- 39. 39 多重共線性の問題について 2020年度 建築計画第二 第10回(沖 拓弥) どういうことか? p個の説明変数のうち,極めて相互に相関の高い変数 が含まれていたり,あるいはある変数が他の変数群と 因果関係にあり,そのために近似的に一次式で表現で きたりする場合。 0 1 1 2 2i i i p pi iy x x xβ β β β ε= + + + + +? 0 2 2i i p pi iy x xβ β β ε= + + + +? ランク落ちが発生
- 40. 40 多重共線性の発見方法 2020年度 建築計画第二 第10回(沖 拓弥) 代表的な方法 p個の説明変数それぞれを目的変数として,それをそれ 以外の説明変数から予測すべく,重回帰分析を反復。 いま,変数 xj を目的変数としたときの重相関係数をRjと すると, で求められる値がひとつの目安であり,通常,VIF>10の とき,多重共線性が見られるとされる(Chatterjee, 1977)。 ???? ?? = 1 ? ???? 2 ?1 VIF:分散拡大要因(Variance inflation factor)
- 41. 41 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定結果の解釈 ①モデルの選択 ②残差分析 ③重相関係数R(自由度調整済み決定係数R2) ④回帰係数の値と符号 ⑤標準化回帰係数 ⑥多重共線性の発生有無の確認 ⑦説明変数の有意性の検証(t値,P値)
- 42. 42 回帰係数の有意性 2020年度 建築計画第二 第10回(沖 拓弥) ? 説明変数が被説明変数に対して影響を及ぼしている かどうかを確認するために,推定した回帰係数の有 意性を確認する必要がある。 ? 対象となる回帰係数βについて,「説明変数xは被説 明変数yに影響を与えていない」(xとyは無相関)とい う帰無仮説を設定する。 H0(帰無仮説): 説明変数xは被説明変数yに影響を与えていない H1(対立仮説): 説明変数xは被説明変数yに影響を与えている 帰無仮説が棄却?対応する回帰係数βは有意
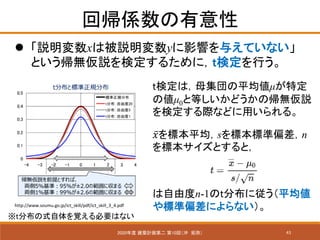
- 43. 43 回帰係数の有意性 2020年度 建築計画第二 第10回(沖 拓弥) ? 「説明変数xは被説明変数yに影響を与えていない」 という帰無仮説を検定するために,t検定を行う。 http://www.soumu.go.jp/ict_skill/pdf/ict_skill_3_4.pdf t検定は,母集団の平均値μが特定 の値μ0と等しいかどうかの帰無仮説 を検定する際などに用いられる。 ※t分布の式自体を覚える必要はない ???を標本平均,sを標本標準偏差,n を標本サイズとすると, は自由度n-1のt分布に従う(平均値 や標準偏差によらない)。
- 44. 44 回帰係数の有意性 2020年度 建築計画第二 第10回(沖 拓弥) ? 直前のスライドで説明したt検定を,回帰係数の有意 性の検定に応用する。 ???????????? = ??? ? ??0 ?? ??? ここで?? ??? は ???の分散を表し, ?? ??? = ???? 2 ∑??=1 ?? ???? ? ??? 2 ???? 2 は回帰の残差(誤差)分散を表し, ???? 2 = ∑??=1 ?? ???? ? ????? 2 ?? ? 2 (導出過程は省略。n-2となるのは,回帰係数分の自由度を除くため。)
- 45. 45 回帰係数の有意性 2020年度 建築計画第二 第10回(沖 拓弥) (つづき) 整理すると, ???????????? = ??? ? ??0 ∑??=1 ?? ???? ? ????? 2 ?? ? 2 ? 1 ∑??=1 ?? ???? ? ??? 2 = ??? ? ??0 ?? ? 2 ∑??=1 ?? ???? ? ????? 2 ∑??=1 ?? ???? ? ??? 2 「説明変数xは被説明変数yに影響を与えていない」とい う帰無仮説を検定したいので,回帰係数 ???がゼロと見な せるかどうか,つまり,??0 = 0としたときの????????????の値に 着目する。
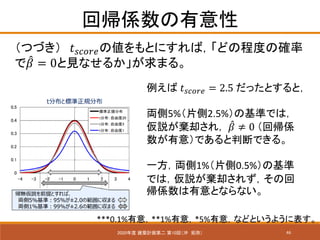
- 46. 46 回帰係数の有意性 2020年度 建築計画第二 第10回(沖 拓弥) (つづき) ????????????の値をもとにすれば,「どの程度の確率 で ??? = 0と見なせるか」が求まる。 例えば ???????????? = 2.5 だったとすると, 両側5%(片側2.5%)の基準では, 仮説が棄却され, ??? ≠ 0 (回帰係 数が有意)であると判断できる。 一方,両側1%(片側0.5%)の基準 では,仮説が棄却されず,その回 帰係数は有意とならない。 ***0.1%有意,**1%有意,*5%有意,などというように表す。
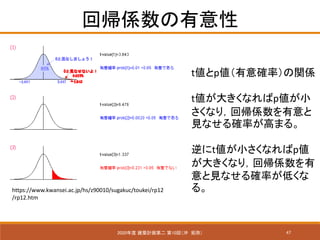
- 47. 47 回帰係数の有意性 2020年度 建築計画第二 第10回(沖 拓弥) https://www.kwansei.ac.jp/hs/z90010/sugakuc/toukei/rp12 /rp12.htm t値とp値(有意確率)の関係 t値が大きくなればp値が小 さくなり,回帰係数を有意と 見なせる確率が高まる。 逆にt値が小さくなればp値 が大きくなり,回帰係数を有 意と見なせる確率が低くな る。
- 48. 48 重回帰分析の基本的な流れ 2020年度 建築計画第二 第10回(沖 拓弥) 推定結果の解釈 ①モデルの選択 ②残差分析 ③重相関係数R(自由度調整済み決定係数R2) ④回帰係数の値と符号 ⑤標準化回帰係数 ⑥多重共線性の発生有無の確認 ⑦説明変数の有意性の検証(t値,P値) ExcelやRなどを使えば,重回帰分析自体は簡単にできるが, 以上の点を必ず確認しましょう
- 49. 49 建築?都市計画分野での実例 2020年度 建築計画第二 第10回(沖 拓弥) 【重回帰分析の例】 1. 河合伸治:ヘドニック?アプローチによる地域住民の選好の推 定ー西武池袋線?東武東上線?田園都市線沿線の賃貸住宅 を事例としてー,社学研論集,Vol.16,pp.180-193,2010.9 2. 樋口恵一?三村泰広?安藤良輔:交通事故と犯罪の発生件数 に影響する地域特性の抽出に関する研究ー豊田市の小学校 区を対象にしたケーススタディー,交通工学論文集,Vol.2, No.2(特集号A),pp.A_193-A_198,2016.2 【数量化理論Ⅰ類の例】 1. 植田裕基?鵤心治?小林剛士:不動産鑑定評価による地域特 性を考慮した住宅地景観の経済価値に関する研究,日本建 築学会中国支部研究報告集,Vol.37,pp.693-696,2014.3
- 50. 50 第10回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 重回帰分析 と 数量化理論Ⅰ類 重回帰分析(Multiple regression analysis) 複数の説明変数X(定量的データ)が目的変数Yに与 える影響の測定や,予測に用いられる方法。 数量化理論Ⅰ類(Hayashi’s quantification theory I) 複数の要因X(定性的データ)が外的基準Yに与える 影響の測定や,予測に用いられる方法。 *定性的データ:名義尺度,順序尺度など Yes/No,ランク
- 51. 51 第10回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 重回帰分析 と 数量化理論Ⅰ類 重回帰分析(Multiple regression analysis) 複数の説明変数X(定量的データ)が目的変数Yに与 える影響の測定や,予測に用いられる方法。 数量化理論Ⅰ類(Hayashi’s quantification theory I) 複数の要因X(定性的データ)が外的基準Yに与える 影響の測定や,予測に用いられる方法。 *定性的データ:名義尺度,順序尺度など Yes/No,ランク
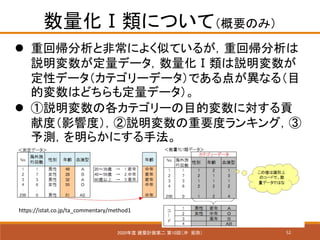
- 52. 52 数量化Ⅰ類について(概要のみ) 2020年度 建築計画第二 第10回(沖 拓弥) ? 重回帰分析と非常によく似ているが,重回帰分析は 説明変数が定量データ,数量化Ⅰ類は説明変数が 定性データ(カテゴリーデータ)である点が異なる(目 的変数はどちらも定量データ)。 ? ①説明変数の各カテゴリーの目的変数に対する貢 献度(影響度),②説明変数の重要度ランキング,③ 予測,を明らかにする手法。 https://istat.co.jp/ta_commentary/method1
- 53. 53 数量化Ⅰ類について(概要のみ) 2020年度 建築計画第二 第10回(沖 拓弥) カテゴリースコアは,重回帰分析の偏回帰係数に相当 する形で使われる。 https://istat.co.jp/ta_commentary/method1 カテゴリー内のカテゴリースコアの差(レンジ) が大きい説明変数ほど重要度が高い。
- 54. 54 建築?都市計画分野での実例 2020年度 建築計画第二 第10回(沖 拓弥) 【重回帰分析の例】 1. 河合伸治:ヘドニック?アプローチによる地域住民の選好の推 定ー西武池袋線?東武東上線?田園都市線沿線の賃貸住宅 を事例としてー,社学研論集,Vol.16,pp.180-193,2010.9 2. 樋口恵一?三村泰広?安藤良輔:交通事故と犯罪の発生件数 に影響する地域特性の抽出に関する研究ー豊田市の小学校 区を対象にしたケーススタディー,交通工学論文集,Vol.2, No.2(特集号A),pp.A_193-A_198,2016.2 【数量化理論Ⅰ類の例】 1. 植田裕基?鵤心治?小林剛士:不動産鑑定評価による地域特 性を考慮した住宅地景観の経済価値に関する研究,日本建 築学会中国支部研究報告集,Vol.37,pp.693-696,2014.3
- 55. 55 重回帰分析以外の回帰分析手法 2020年度 建築計画第二 第6回(沖 拓弥) Esriジャパン:ランダムフォレストによる土地取引価格の予測, https://www.arcgis.com/apps/Cascade/index.html?appid=24f20 d55c94144b99d799fae3f1c426f ? 重回帰分析は,シンプルでありながら説明力が高い ため,広く使われているが,限界もある。 ? 特に,説明変数xの線形和で表す構造となっているこ とから,非線形の現象を記述することには適さない (cf:非線形回帰モデル)。 ? 多変数を考慮した回帰分析手法には,重回帰分析 以外にも様々な手法がある。近年は,機械学習を用 いた回帰分析も行われる。
- 56. 56 第10回のテーマ 2020年度 建築計画第二 第10回(沖 拓弥) 重回帰分析 と 数量化理論Ⅰ類 重回帰分析(Multiple regression analysis) 複数の説明変数X(定量的データ)が目的変数Yに与 える影響の測定や,予測に用いられる方法。 数量化理論Ⅰ類(Hayashi’s quantification theory I) 複数の要因X(定性的データ)が外的基準Yに与える 影響の測定や,予測に用いられる方法。 *定性的データ:名義尺度,順序尺度など Yes/No,ランク
- 57. 57 参考文献(第9?10回) 2020年度 建築計画第二 第10回(沖 拓弥) 1. 吉田光雄:重回帰分析における多重共線性とRidge回帰に ついて,大阪大学人間科学部紀要,13,pp.227-242, 1987.3 2. 小西貞則:多変量解析入門ー線形から非線形へー,岩波 書店,2020
- 58. 58 6/5小レポート課題 2020年度 建築計画第二 第10回(沖 拓弥) 建築?都市計画分野で,重回帰分析または 数量化Ⅰ類に関わる論文を1編読み,A4 用紙1ページ以内に要約する。 著者,タイトル,雑誌名,年,ページ 推定式,変数一覧,推定結果など図表を 載せ,授業内容とも関連させながら自分な りの感想を述べる。 6/12(金)授業開始までにOCW-iに提出