第2回顿础搁惭勉强会
- 1. DARM勉強会#2 2013.03.02 R?RStudioの導入 Multiple Regression 広島大学総合科学研究科 博士課程後期2年 竹林 由武
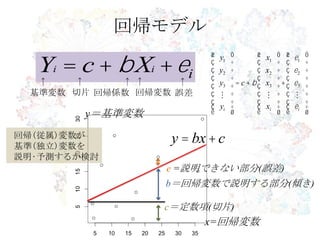
- 2. 回帰モデル Yi = c + b Xi + ei ? y1 ? ? x1 ? ? e1 ? ? ÷ ? ÷ ? ÷ ? y2 ÷ ? x2 ÷ ? e2 ÷ ? ÷ ? ÷ ? ÷ ↑ ↑ ↑↑ ↑ ? y3 ÷ = c + b ? x3 ÷ + ? e3 ÷ 基準変数 切片 回帰係数 回帰変数 誤差 ? ? ÷ ? ? ÷ ? ? ÷ R?RStudioの導入 y=基準変数 ? ? è ÷ yi ÷ ? ? ? è ÷ ? xi ÷ ? ? è ÷ ei ÷ ? 回帰(従属)変数が 基準(独立)変数を y = bx + c 説明?予測するか検討 e =説明できない部分(誤差) b=回帰変数で説明する部分(傾き) c=定数項(切片) x=回帰変数
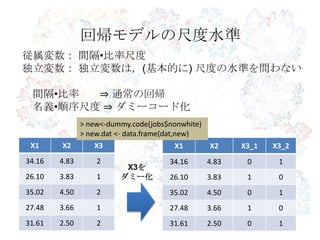
- 3. 回帰モデルの尺度水準 従属変数: 間隔?比率尺度 独立変数: 独立変数は,(基本的に) 尺度の水準を問わない 間隔?比率 ? 通常の回帰 名義?順序尺度 ? ダミーコード化 > new<-dummy.code(jobs$nonwhite) > new.dat <- data.frame(dat,new) X1 X2 X3 X1 X2 X3_1 X3_2 34.16 4.83 2 34.16 4.83 0 1 X3を 26.10 3.83 1 ダミー化 26.10 3.83 1 0 35.02 4.50 2 35.02 4.50 0 1 27.48 3.66 1 27.48 3.66 1 0 31.61 2.50 2 31.61 2.50 0 1
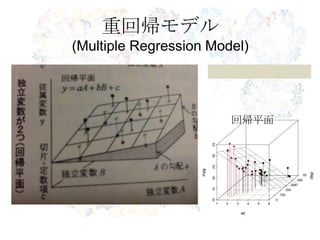
- 4. 重回帰モデル (Multiple Regression Model) Yi β 0 β1 X 1i ... βkXki εi ↑ 基準変数 ↑ R?RStudioの導入 ↑ 切片 回帰係数 ↑ 回帰変数 ↑ 誤差 (従属変数 or アウトカム) (独立変数 or 予測変数) 目 的 複数の回帰変数が基準変数を説明(予測)するか検討 X1 β1 β2 X2 Y β3 X3
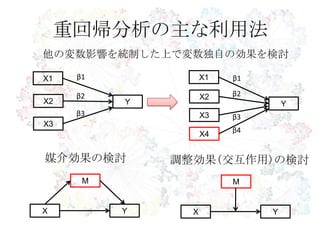
- 6. 重回帰分析の主な利用法 他の変数影響を統制した上で変数独自の効果を検討 X1 β1 X1 β1 β2 X2 β2 X2 Y Y β3 X3 β3 X3 β4 X4 媒介効果の検討 調整効果(交互作用)の検討 M M X Y X Y
- 7. Reporting Guideline Kelley, K. & Maxwell, S. E. (2008). Multiple Reggression. In G. R., Hancock & R. O. Mueller (Eds.), The Reviewer’s Guide to Quantitative Methods in the Social Sciences. (pp. R?RStudioの導入 281-288) New York: Routledge. 重回帰分析を使う時は, 次の14項目を守りましょ う!! Maxwell, S. E. 師 弟 Kelley, K 効果量や信頼区間を算出するRpackage”MBESS”の作成者
- 8. Reporting Guideline (Kelly & Maxwell, 2008) 1. 研究の目的や重回帰がどのように役立つかが明示されてる 2. 各変数を独立変数に含める理論的,慣習的な理由が 正当化されているべき R?RStudioの導入 3. 効果量の算出と解釈のための手続きが記述されている 4. 重回帰分析の前提や結果の推論が明示されている 5. 変数の選択法が正当化されている 6. 検定力,正確性,再現性といった観点から 全ての分析においてsample sizeが正当化されている 7. 重回帰モデルがどのように解釈されるべきか伝えるために 各基準?回帰変数が詳細に記述されている
- 9. 1. 研究の目的 1.研究の目的や重回帰が 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 どのように役立つかが明示されてる 重回帰分析の使用目的 (説明 vs 予測) ①説明: 個々の変数とアウトカムの関係性を理解したい (主に現象の理解が目的) R?RStudioの導入 e.g. 攻撃性に関与するパーソナリティ要因 ②予測: 特定の変数がアウトカムに作用する程度が知りたい (主に慣習的応用(practical aplication)が目的) e.g. 大学での成績による収入の予測 分析の目的が説明or予測,または両者なのか明記すべし ※サンプルから得られた情報を母集団に一般化したい時に統計的推論は重要 目的が真に予測である場合,推論手続きは厳密には必要ではないが, いずれにせよ,関心の母集団についての情報は呈示せよ
- 10. 1. 2. 研究の目的 回帰変数の正当化 2.各変数を回帰変数に含める理論的, 3. 基準?回帰変数の記述 4. 5. 効果サイズ 前提 慣習的な理由が正当化されている 6. 変数選択の正当性 7. サンプルサイズの正当性 べき 検証的研究 目的が明確な研究:理論的に正当化された尐数の変数で仮説検証 ?回帰分析の前提が満たされた場合に,P値や効果量の信頼区間は有意 味 R?RStudioの導入 探索的研究 拡散的な研究:理論的に正当化されていない多くの変数で仮説生成 ?P値や効果量の信頼区間は将来の検証的研究の足掛かりとなる値 (正確な値と言えない) ?多くの帰無仮説を検定することになるので,検定の多重性が生じる 探索的な研究と検証的な研究の区別を明確にすべき ※探索的な方法は予測では効果的なこともあるが(stepwise法など),
- 11. 1. 研究の目的 3. 重回帰モデルの解釈の仕方を伝えるた めに 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性各基準?回帰変数が詳細に記述されて サンプルサイズの正当性 いる 以下の情報を記載すべし ? 平均と共分散行列(or相関行列) (解析に使用した全ての変数) ? 変数のタイプ (categorical or continuous) ? 尺度得点の範囲 R?RStudioの導入 ? 変数のコーディング方法 (カテゴリ変数の時) ? 信頼性 0.25 連続変数を2値変数化してはいけない 0.20 0.15 (多分岐変数化もダメ(polytomize)) y 0.10 0.05 ①個人のtaxonやタイプが明確である場合はOK 0.00 -6 -4 -2 0 2 4 6 x ②変数の分布の歪度が高い場合はOK
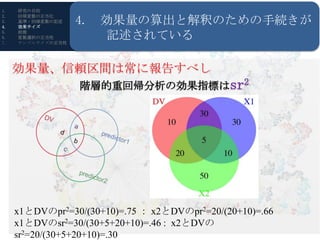
- 12. 1. 研究の目的 4. 効果量の算出と解釈のための手続きが 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 記述されている 効果量、信頼区間は常に報告すべし Omnibus (総合効果) : 一般的には決定係数(R2) = 重相関係数の2乗 R?RStudioの導入 R2=(a+b+c)/(a+b+c+d) 目的が説明の場合: DV a predictor1 自由度調整済み決定係数 d 2 RA max 0, 1 (1 R 2 ) N 1 , b N K 1 c 目的が予測かつ結果の一般化: population cross validtyによる補正 predictor2 NR 2 K RC R( N K )
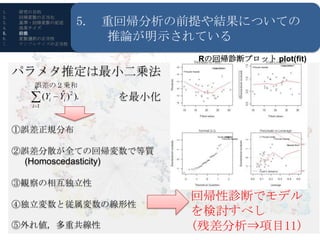
- 13. 1. 研究の目的 4. 効果量の算出と解釈のための手続きが 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 記述されている 効果量、信頼区間は常に報告すべし 階層的重回帰分析の効果指標はsr2 R?RStudioの導入 (squared semi-partial (part) correlation:sr2) pr2=a/(a+d) ? 偏相関^2 =c/(c+d) a predictor1 sr2=a/(a+b+c+d) DV ? 部分相関^2 =c/(a+b+c+d) d b 基準変数の全分散のうち,一 c つの回帰変数以外で説明され る分散を除いた分 predictor2 = 一つの回帰係数独自の説明?予測力
- 14. 1. 研究の目的 4. 効果量の算出と解釈のための手続きが 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 記述されている 効果量、信頼区間は常に報告すべし 階層的重回帰分析の効果指標はsr2 R?RStudioの導入 x1とDVのpr2=30/(30+10)=.75 : x2とDVのpr2=20/(20+10)=.66 x1とDVのsr2=30/(30+5+20+10)=.46 : x2とDVの sr2=20/(30+5+20+10)=.30
- 15. 1. 研究の目的 Reporting 4.4. 効果量の算出と解釈のための手続きが 2. 回帰変数の正当化 3. 4. 基準?回帰変数の記述 Guideline 効果サイズ 効果量の算出と解釈のための手続きが記述されている 5. 6. 7. 前提 & Keselman) (Lix 変数選択の正当性 サンプルサイズの正当性 記述されている Targeted (局所効果): (非)標準化回帰係数 ※標準?非昇順ともに乗せる(with 信頼区間) R?RStudioの導入 sY 非標準化回帰係数 * = 標準化回帰係数 sXk sX k 標準化回帰係数 * = 非標準化回帰係数 sY どちらの信頼区間もMBESSでだせますが何か?
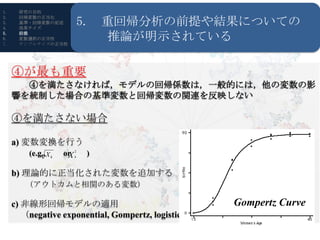
- 16. 1. 研究の目的 5. 重回帰分析の前提や結果についての 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 推論が明示されている Rの回帰診断プロット plot(fit) パラメタ推定は最小二乗法 誤差の2乗和 N ? 2 を最小化 (Y i 1 i iY ) ). R?RStudioの導入 ①誤差正規分布 ②誤差分散が全ての回帰変数で等質 (Homoscedasticity) ③観察の相互独立性 回帰性診断でモデル ④独立変数と従属変数の線形性 を検討すべし ⑤外れ値, 多重共線性 (残差分析?項目11)
- 17. 1. 研究の目的 Reporting 5.5. 重回帰分析の前提や結果についての 2. 回帰変数の正当化 3. 4. 基準?回帰変数の記述 Guideline 効果サイズ 重回帰分析の前提や結果の推論が明示されている 5. 6. 7. 前提 (Lix & Keselman) 変数選択の正当性 サンプルサイズの正当性 推論が明示されている ④が最も重要 ④を満たさなければ,モデルの回帰係数は,一般的には,他の変数の影 響を統制した場合の基準変数と回帰変数の関連を反映しない R?RStudioの導入 ④を満たさない場合 a) 変数変換を行う (e.g., X k or 2 Xk ) b) 理論的に正当化された変数を追加する (アウトカムと相関のある変数) c) 非線形回帰モデルの適用 Gompertz Curve (negative exponential, Gompertz, logistic)
- 18. 1. 研究の目的 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 5. 効果サイズ 前提 6. 変数の選択法が正当化されている。 6. 変数選択の正当性 7. サンプルサイズの正当性 a) 全ての分析が理論ドライブ 理想的。標的の研究仮説と標的の統計解析が合致。 b) モデルの比較を行う R?RStudioの導入 初期のモデルに回帰変数を追加しR2の増分が有意か検討 (階層的重回帰) c) ステップワイズ法を用いる (データドライブ) 研究の目的が探索的であることを明記 手続きを明記 (forward selection, backward selection … ) 選択基準を明記 (統計的に有意なR2の変化量) 使用したパッケージ/プログラムを明記 d) 様々な探索的モデルや方法をフィットさせる (1) 回帰変数の中から主要な関心のある回帰変数を同定する (2) アウトカム変数に対して重要な回帰変数を同定する (3) 予測 ※ 交絡要因は回帰変数に含めるべき
- 19. 1. 研究の目的 7.検定力,正確性,再現性の観点から全 て 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 の分析のサンプル数が正当化されてい る 検定力分析 目的:誤った帰無仮説が望ましい確率によって棄却されること R?RStudioの導入 パラメータ推定の正確性 (AIPE: accuracy in parameter estimation) 目的:母集団値の正確な推定を得ること 研究目的が“予測”? omnibusの効果量(R2)に基づいて例数設計 研究目的が“説明”? targetedの効果量(B, β)に基づいて例数設計 検定力と正確度のどちらも高い例数設計が理想的
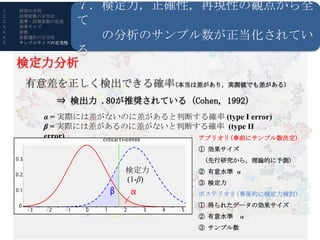
- 20. 1. 研究の目的 7.検定力,正確性,再現性の観点から全 て 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 の分析のサンプル数が正当化されてい 変数選択の正当性 サンプルサイズの正当性 る 検定力分析 有意差を正しく検出できる確率(本当は差があり,実測値でも差がある) R?RStudioの導入 ? 検出力 .80が推奨されている (Cohen, 1992) α = 実際には差がないのに差があると判断する確率 (type I error) β = 実際には差があるのに差がないと判断する確率 (type II error) アプリオリ(事前にサンプル数決定) ① 効果サイズ (先行研究から,理論的に予測) 検定力 ② 有意水準 α (1-β) ③ 検定力 ポステリオリ(事後的に検定力検討) ① 得られたデータの効果サイズ ② 有意水準 α ③ サンプル数
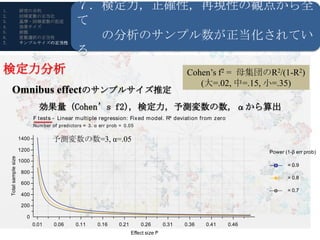
- 21. 1. 研究の目的 7.検定力,正確性,再現性の観点から全 て 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 の分析のサンプル数が正当化されてい る 検定力分析 Cohen’s f2 = 母集団のR2/(1-R2) (大=.02, 中=.15, 小=.35) Omnibus effectのサンプルサイズ推定 R?RStudioの導入 効果量 (Cohen’s f2), 検定力,予測変数の数,αから算出 F tests - Linear m ultiple regression: Fix ed m odel. R? deviation from zero Num ber of predictors = 3. α err prob = 0.05 1400 予測変数の数=3, α=.05 1200 Power (1-β err prob) Total sample size 1000 = 0.9 800 = 0.8 600 = 0.7 400 200 0 0.01 0.06 0.11 0.16 0.21 0.26 0.31 0.36 0.41 0.46 Effect size f?
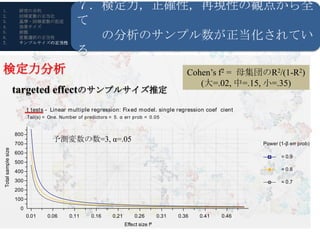
- 22. 1. 研究の目的 7.検定力,正確性,再現性の観点から全 て 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 の分析のサンプル数が正当化されてい る 検定力分析 Cohen’s f2 = 母集団のR2/(1-R2) (大=.02, 中=.15, 小=.35) targeted effectのサンプルサイズ推定 R?RStudioの導入 t tests - Linear m ultiple regression: Fix ed model. single regression coef cient Tail(s) = One. Num ber of predictors = 5. α err prob = 0.05 800 700 予測変数の数=3, α=.05 Power (1-β err prob) Total sample size 600 = 0.9 500 400 = 0.8 300 = 0.7 200 100 0 0.01 0.06 0.11 0.16 0.21 0.26 0.31 0.36 0.41 0.46 Effect size f?
- 23. 1. 研究の目的 7.検定力,正確性,再現性の観点から全 て 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 の分析のサンプル数が正当化されてい る パラメータ推定の正確性 (AIPE: accuracy in parameter estimation) R?RStudioの導入 目的:母集団値の正確な推定を得ること 信頼区間の区間幅(の期待値)や信頼限界比が一定値以下になるように サンプルサイズを設計 (永田,2003) Kelley and Maxwell (2003)より抜粋 1) 有意だけど不正確 2) 有意で正確 3) 有意じゃないし不正確 4) 有意じゃなくて正確 結果が有意であっても,パラメタの信頼区間が広いと,
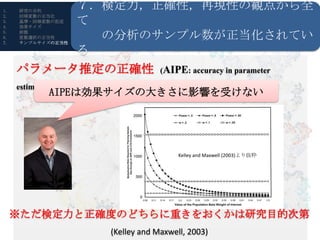
- 24. 1. 研究の目的 7.検定力,正確性,再現性の観点から全 て 2. 回帰変数の正当化 3. 基準?回帰変数の記述 4. 効果サイズ 5. 6. 7. 前提 変数選択の正当性 サンプルサイズの正当性 の分析のサンプル数が正当化されてい る パラメータ推定の正確性 (AIPE: accuracy in parameter estimation) AIPEは効果サイズの大きさに影響を受けない R?RStudioの導入 Kelley and Maxwell (2003)より抜粋 ※ただ検定力と正確度のどちらに重きをおくかは研究目的次第 (Kelley and Maxwell, 2003)