Θέματα φυσικής - πανελλαδικές 2022
- 1. ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΛΟΣ 1ΗΣ ΑΠΟ 7 ΣΕΛΙΔΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΠΑΡΑΣΚΕΥΗ 10 ΙΟΥΝΙΟΥ 2022 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στην επιλογή σας, η οποία συμπληρώνει σωστά την ημιτελή πρόταση. A1. Όταν δύο σφαίρες μικρών διαστάσεων, ίδιας μάζας, που κινούνται σε λείο οριζόντιο δάπεδο, συγκρουστούν έκκεντρα και ελαστικά, τότε: α) ανταλλάσσουν ταχύτητες. β) ελαττώνεται η κινητική ενέργεια του συστήματος των δύο σφαιρών. γ) διατηρείται η ορμή του συστήματος των δύο σφαιρών. δ) δεν μεταβάλλεται η ορμή της κάθε σφαίρας κατά την κρούση. Μονάδες 5 A2. Ιδανικό ρευστό ρέει σε οριζόντιο σωλήνα μεταβλητής διατομής. Η διατομή του σωλήνα σε μια περιοχή Α είναι τετραπλάσια της διατομής του σωλήνα σε μια άλλη περιοχή Β. Αν η ταχύτητα του ρευστού στην περιοχή Α είναι ίση με u, τότε η ταχύτητα στην περιοχή Β είναι: α) u 4 γ) 2u β) u δ) 4u Μονάδες 5 A3. Αν το πλάτος της έντασης του εναλλασσόμενου ρεύματος που διαρρέει έναν αντιστάτη υποδιπλασιαστεί, τότε ο ρυθμός με τον οποίο ο αντιστάτης αποδίδει θερμότητα στο περιβάλλον: α) υποδιπλασιάζεται. β) διπλασιάζεται. γ) υποτετραπλασιάζεται. δ) τετραπλασιάζεται. Μονάδες 5 A4. Σε μια απλή αρμονική ταλάντωση, όταν ο ταλαντωτής κινείται προς τη θέση ισορροπίας: α) η δυναμική ενέργεια του ταλαντωτή αυξάνεται. β) το μέτρο της επιτάχυνσης του ταλαντωτή μειώνεται. γ) το μέτρο της ταχύτητας του ταλαντωτή μειώνεται. δ) το μέτρο της δύναμης επαναφοράς στον ταλαντωτή αυξάνεται. Μονάδες 5
- 2. ΑΡΧΗ 2ΗΣ ΣΕΛΙΔΑΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΛΟΣ 2ΗΣ ΑΠΟ 7 ΣΕΛΙΔΕΣ Α5. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη. α) Αν διπλασιάσουμε το μέτρο καθεμιάς από τις δύο δυνάμεις ενός ζεύγους δυνάμεων, χωρίς να αλλάξουμε την απόσταση των φορέων των δυνάμεων, τότε το μέτρο της ροπής του ζεύγους των δυνάμεων τετραπλασιάζεται. β) Αν μέσα σε σωληνοειδές, που διαρρέεται από ρεύμα σταθερής έντασης, τοποθετήσουμε πυρήνα μαλακού σιδήρου, οι δυναμικές γραμμές του μαγνητικού πεδίου στο εσωτερικό του πυρήνα θα πυκνώσουν. γ) Αν μικρή σφαίρα συγκρουστεί κάθετα και ελαστικά με λείο κατακόρυφο τοίχο έχοντας ορμή μέτρου p, η μεταβολή του μέτρου της ορμής της είναι ίση με 2p. δ) Η Γη έχει ιδιοστροφορμή (σπιν) εξαιτίας της περιστροφής της γύρω από τον άξονά της. ε) Σε μια εξαναγκασμένη ταλάντωση με σταθερά απόσβεσης b, το μέγιστο πλάτος της ταλάντωσης στην περιοχή συντονισμού εξαρτάται από την τιμή της σταθεράς b. Μονάδες 5 ΘΕΜΑ Β Β1. Σώμα Σ μικρών διαστάσεων και μάζας m ισορροπεί δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο (Σχήμα 1). Εκτελούμε δύο πειράματα: Σχήμα 1 Πείραμα 1 Μετακινούμε το σώμα Σ στη θέση φυσικού μήκους (θ.φ.μ.) του ελατηρίου, το αφήνουμε ελεύθερο και αυτό εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D = k και πλάτος 1 A . Πείραμα 2 Στην αρχική θέση ισορροπίας (θ.ι.) του σώματος Σ ασκείται σε αυτό, συνεχώς, κατακόρυφη δύναμη F μέτρου F mg = με φορά προς τα πάνω και τότε το σώμα εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D = k και πλάτος 2 A . Για τα πλάτη 1 A και 2 A των παραπάνω πειραμάτων, ισχύει: i. = 1 2 A A ii. = 1 2 1 A A 2 iii. = 1 2 A 2A α) Να επιλέξετε τη σωστή απάντηση. Μονάδες 2 β) Να δικαιολογήσετε την επιλογή σας. Μονάδες 6
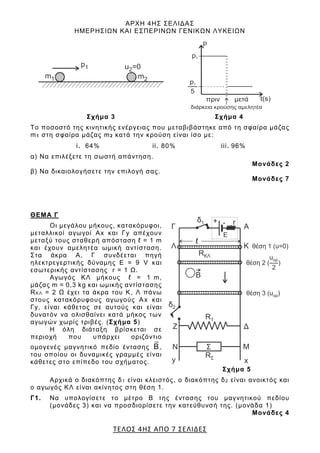
- 3. ΑΡΧΗ 3ΗΣ ΣΕΛΙΔΑΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΛΟΣ 3ΗΣ ΑΠΟ 7 ΣΕΛΙΔΕΣ Β2. Ένα ανοιχτό δοχείο μεγάλου όγκου με κατακόρυφα τοιχώματα ηρεμεί ακλόνητο πάνω σε οριζόντιο δάπεδο. Το δοχείο περιέχει νερό, το οποίο θεωρείται ιδανικό ρευστό, μέχρι ύψους Η πάνω από τη βάση του. Το δοχείο έχει στο πλευρικό του τοίχωμα δύο οπές (1) και (2) ίδιου εμβαδού διατο μής Α, το οποίο είναι αμελητέο σε σύγκριση με το εμβαδόν της ελεύθερης επιφάνειας του νερού. Οι δύο οπές (1) και (2) βρίσκονται σε ύψη 5H 6 και H 3 , αντίστοιχα, από τον πυθμένα του δοχείου (Σχήμα 2). Όταν είναι ανοικτή μόνο η οπή (1), όγκος υγρού V εκρέει από το δοχείο σε χρονικό διάστημα 1 Δt . Όταν είναι ανοικτές και οι δύο οπές (1) και (2), ο ίδιος όγκος V εκρέει σε χρονικό διάστημα 2 Δt . Σχήμα 2 Ο λόγος των χρονικών διαστημάτων 2 1 Δt Δt είναι ίσος με: i. 1 2 ii. 1 3 iii. 1 4 (Θεωρήστε ότι κατά τις εκροές του υγρού, η ταχύτητα της επιφάνειας του υγρού είναι μηδενική). α) Να επιλέξετε τη σωστή απάντηση. Μονάδες 2 β) Να δικαιολογήσετε την επιλογή σας. Μονάδες 6 Β3. Σφαίρα μάζας m1 κινείται με ορμή μέτρου p1 και συγκρούεται, κεντρικά και ελαστικά, με ακίνητη σφαίρα μάζας m2, όπως φαίνεται στο Σχήμα 3. Η γραφική παράσταση της ορμής της σφαίρας m1 φαίνεται στο Σχήμα 4.
- 4. ΑΡΧΗ 4ΗΣ ΣΕΛΙΔΑΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΛΟΣ 4ΗΣ ΑΠΟ 7 ΣΕΛΙΔΕΣ Σχήμα 3 Σχήμα 4 Το ποσοστό της κινητικής ενέργειας που μεταβιβάστηκε από τη σφαίρα μάζας m1 στη σφαίρα μάζας m2 κατά την κρούση είναι ίσο με: i. 64% ii. 80% iii. 96% α) Να επιλέξετε τη σωστή απάντηση. Μονάδες 2 β) Να δικαιολογήσετε την επιλογή σας. Μονάδες 7 ΘΕΜΑ Γ Οι μεγάλου μήκους, κατακόρυφοι, μεταλλικοί αγωγοί Αx και Γy απέχουν μεταξύ τους σταθερή απόσταση ℓ = 1 m και έχουν αμελητέα ωμική αντίσταση. Στα άκρα Α, Γ συνδέεται πηγή ηλεκτρεγερτικής δύναμης Ε = 9 V και εσωτερικής αντίστασης r = 1 Ω. Αγωγός ΚΛ μήκους ℓ = 1 m, μάζας m = 0,3 kg και ωμικής αντίστασης RΚΛ = 2 Ω έχει τα άκρα του Κ, Λ πάνω στους κατακόρυφους αγωγούς Αx και Γy, είναι κάθετος σε αυτούς και είναι δυνατόν να ολισθαίνει κατά μήκος των αγωγών χωρίς τριβές. (Σχήμα 5) Η όλη διάταξη βρίσκεται σε περιοχή που υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης B, του οποίου οι δυναμικές γραμμές είναι κάθετες στο επίπεδο του σχήματος. Σχήμα 5 Αρχικά ο διακόπτης δ1 είναι κλειστός, ο διακόπτης δ2 είναι ανοικτός και ο αγωγός ΚΛ είναι ακίνητος στη θέση 1. Γ1. Να υπολογίσετε το μέτρο Β της έντασης του μαγνητικού πεδίου (μονάδες 3) και να προσδιορίσετε την κατεύθυνσή της. (μονάδα 1) Μονάδες 4
- 5. ΑΡΧΗ 5ΗΣ ΣΕΛΙΔΑΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΛΟΣ 5ΗΣ ΑΠΟ 7 ΣΕΛΙΔΕΣ Στο κάτω μέρος της διάταξης, μεταξύ των σημείων Ζ και Δ, είναι συνδεδεμένος αντιστάτης με ωμική αντίσταση R1 = 3 Ω και στα σημεία Μ, Ν είναι συνδεδεμένη θερμική συσκευή Σ ωμικής αντίστασης RΣ, η οποία όταν στα άκρα της Μ, Ν έχει τάση ίση με 6 V λειτουργεί κανονικά αποδίδοντας θερμική ισχύ 6 W. Ανοίγουμε τον διακόπτη δ1, κλείνοντας ταυτόχρονα τον διακόπτη δ2 και ο αγωγός ΚΛ αρχίζει να κατέρχεται παραμένοντας συνεχώς οριζόντιος χωρίς τα άκρα του Κ, Λ να χάνουν την επαφή με τους αγωγούς Αx και Γy. Γ2. Έστω ότι ο αγωγός ΚΛ έχει αποκτήσει οριακή ταχύτητα ορ u στη θέση 3. Να δικαιολογήσετε το είδος της κίνησης που εκτελεί ο αγωγός ΚΛ από τη θέση 1 έως τη θέση 3 (μονάδες 3) και να υπολογίσετε τη σταθερή οριακή ταχύτητα ορ u . (μονάδες 6) Μονάδες 9 Γ3. Να υπολογίσετε τον ρυθμό μεταβολής της ορμής του αγωγού στη θέση 2, στην οποία η ταχύτητά του είναι ίση με ορ u 2 . Μονάδες 6 Γ4. Όταν ο αγωγός έχει αποκτήσει την οριακή του ταχύτητα, να εξετάσετε αν η θερμική συσκευή Σ λειτουργεί κανονικά. Μονάδες 6 • Δίνεται η επιτάχυνση της βαρύτητας: g = 10 m/s2 • Η αντίσταση του αέρα θεωρείται αμελητέα. • Το σχήμα δεν είναι υπό κλίμακα. ΘΕΜΑ Δ Λεπτή, άκαμπτη, ομογενής και ισοπαχής ράβδος ΑΒ μάζας Μρ = 3 kg και μήκους ℓ = 2 m, φέρει στο άκρο της Α σφαιρίδιο Σ μάζας m = 1 kg, αμελητέων διαστάσεων, και ισορροπεί σε πλάγια θέση με τη βοήθεια κατακόρυφου υποστηρίγματος, το οποίο έχουμε στερεώσει στο λείο οριζόντιο δάπεδο (1). Η ράβδος ακουμπά με το άκρο της Β στο δάπεδο (1) σχηματίζοντας γωνία φ, όπου ημφ = 0,8 και συνφ = 0,6. Η κορυφή του υποστηρίγματος συνδέεται με την ράβδο στο μέσον της Γ με άρθρωση και το σύστημα ράβδος-σφαιρίδιο μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το σημείο Γ (κάθετα στο επίπεδο του σχήματος). Με τη βοήθεια του οριζόντιου, αβαρούς και μη εκτατού νήματος (1) έχουμε συνδέσει το σφαιρίδιο Σ με το ανώτερο σημείο Δ ομογενούς τροχαλίας μάζας Μτ = 7 kg και ακτίνας R = 0,4 m. Η τροχαλία σε απόσταση r = 0,3 m από το κέντρο της Ο έχει ένα λεπτό κυκλικό αυλάκι στο οποίο έχουμε τυλίξει πολλές φορές αβαρές και μη εκτατό νήμα (2). Στο άκρο Ζ του νήματος (2) ασκούμε σταθερή δύναμη F. Όλη η διάταξη ισορροπεί στο ίδιο κατακόρυφο επίπεδο.
- 6. ΑΡΧΗ 6ΗΣ ΣΕΛΙΔΑΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΛΟΣ 6ΗΣ ΑΠΟ 7 ΣΕΛΙΔΕΣ Σχήμα 6 Δ1. Αν το μέτρο της δύναμης που ασκεί το νήμα (1) στο σφαιρίδιο Σ είναι 10,5 Ν, να υπολογίσετε το μέτρο της δύναμης που δέχεται η ράβδος στο άκρο της Β από το λείο δάπεδο (1). Μονάδες 4 Τη χρονική στιγμή t0 = 0 s κόβουμε το νήμα (1). Το σύστημα ράβδος – σφαιρίδιο Σ αρχίζει να περιστρέφεται σε κατακόρυφο επίπεδο, χάνοντας την επαφή του με το δάπεδο (1). Δ2. Να υπολογίσετε τον ρυθμό μεταβολής της στροφορμής της ράβδου ως προς τον άξονα περιστροφής της, αμέσως μετά το κόψιμο του νήματος (1) και ενώ η ράβδος έχει χάσει την επαφή της με το λείο δάπεδο (1). Μονάδες 6 Κατά την περιστροφή του συστήματος ράβδου–σφαιριδίου Σ, το σφαιρίδιο Σ χτυπά στο οριζόντιο δάπεδο. Η γωνιακή ταχύτητα του συστήματος αμέσως μετά την κρούση έχει μέτρο ω 2 , όπου ω το μέτρο της γωνιακής ταχύτητας ακριβώς πριν την κρούση. Δ3. Να υπολογίσετε το μέτρο της μεταβολής της στροφορμής ΔL του συστήματος ράβδος–σφαιρίδιο Σ και να σχεδιάσετε το διάνυσμα ΔL. Μονάδες 5 Η τροχαλία, αμέσως μετά τη χρονική στιγμή t0 = 0 s, αρχίζει να κυλίεται χωρίς να ολισθαίνει στο οριζόντιο δάπεδο (2) με την επίδραση της δύναμης F, το μέτρο της οποίας είναι 12 Ν. Ο άξονας περιστροφής της παραμένει συνεχώς οριζόντιος και κάθετος στο επίπεδο του σχήματος. Δ4. Να υπολογίσετε την επιτάχυνση του κέντρου μάζας της τροχαλίας. Μονάδες 4 Δ5. Να υπολογίσετε το έργο της δύναμης F από τη χρονική στιγμή t0 = 0 s έως τη χρονική στιγμή t1 = 2 s. Μονάδες 6
- 7. ΑΡΧΗ 7ΗΣ ΣΕΛΙΔΑΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΤΕΛΟΣ 7ΗΣ ΑΠΟ 7 ΣΕΛΙΔΕΣ Δίνονται: • η επιτάχυνση της βαρύτητας g = 10 m/s2 • η ροπή αδράνειας ράβδου ως προς άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος σε αυτή: 2 cm(ρ) ρ 1 I M 12 = • η ροπή αδράνειας τροχαλίας ως προς τον άξονά της: 2 cm(τ) τ 1 I M R 2 = Να θεωρήσετε ότι: • η κρούση είναι ακαριαία • η αντίσταση του αέρα θεωρείται αμελητέα για όλα τα σώματα • κατά την κρούση, δεν έχουμε απώλεια μάζας • το σχήμα δεν είναι υπό κλίμακα ΟΔΗΓΙΕΣ (για τους εξεταζομένους) 1. Στο εξώφυλλο του τετραδίου να γράψετε το εξεταζόμενο μάθημα. Στο εσώφυλλο πάνω-πάνω να συμπληρώσετε τα ατομικά στοιχεία μαθητή. Στην αρχή των απαντήσεών σας να γράψετε πάνω-πάνω την ημερομηνία και το εξεταζόμενο μάθημα. Να μην αντιγράψετε τα θέματα στο τετράδιο και να μη γράψετε πουθενά στις απαντήσεις σας το όνομά σας. 2. Να γράψετε το ονοματεπώνυμό σας στο πάνω μέρος των φωτοαντιγράφων αμέσως μόλις σας παραδοθούν. Τυχόν σημειώσεις σας πάνω στα θέματα δεν θα βαθμολογηθούν σε καμία περίπτωση. Κατά την αποχώρησή σας να παραδώσετε μαζί με το τετράδιο και τα φωτοαντίγραφα. 3. Να απαντήσετε στο τετράδιό σας σε όλα τα θέματα μόνο με μπλε ή μόνο με μαύρο στυλό με μελάνι που δεν σβήνει. Για τα σχήματα μπορεί να χρησιμοποιηθεί και μολύβι. 4. Κάθε απάντηση επιστημονικά τεκμηριωμένη είναι αποδεκτή. 5. Διάρκεια εξέτασης: τρεις (3) ώρες μετά τη διανομή των φωτοαντιγράφων. 6. Ώρα δυνατής αποχώρησης: 10.00 π.μ. ΣΑΣ ΕΥΧΟΜΑΣΤΕ KΑΛΗ ΕΠΙΤΥΧΙΑ ΤΕΛΟΣ ΜΗΝΥΜΑΤΟΣ