2022年度秋学期 画像情報処理 第3回 フーリエ級数とフーリエ変換 (2022. 10. 7)
- 2. 2 フーリエ級数
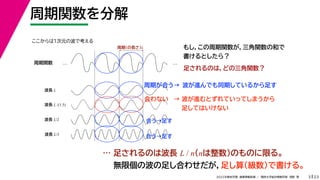
- 3. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期関数を分解 3 ここからは1次元の波で考える 周期関数 … … もし,この周期関数が,三角関数の和で 書けるとしたら? 周期(の長さ)L 波長 L 波長 L/2 波長 L/3 … 足されるのは波長 L / n(nは整数)のものに限る。 無限個の波の足し合わせだが,足し算(級数)で書ける。 波長 L /(1.5) 合う→足す 合う→足す 合わない 周期が合う→ 波が進んでも同期しているから足す → 波が進むとずれていってしまうから 足してはいけない 足されるのは,どの三角関数?
- 4. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 「無限個だが,足し算で書ける」 4 周期関数 f(x) … … 周期関数 f(x)が,三角関数の和で書けるとしたら,足されるのは 周期 L 波長 L 波長 L/3 … 足されるのは波長 L / n(nは整数)のものに限るから, 無限個の三角関数を足すのだけれども このように「項」を並べることができる f(x) = + 波長 L/2 + + … + + … 波長 L/n 「級数」という
- 5. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期関数=三角関数の級数 5 なのですが… 三角関数は計算が面倒。 指数関数なら計算が簡単 f(x) = a0 + a1 cos(2π 1 L x) + a2 cos(2π 2 L x) + … + an cos(2π n L x) + … 波長 L 波長 L/2 波長 L/n cos x cos y = 1 2 {cos(x + y) + cos(x ? y)} ax ay = ax+y かけ算=指数の足し算
- 6. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 三角関数と指数関数の関係 6 exp(iω) = cos ω + i sin ω オイラーの式 cos ω = exp(iω) + exp(?iω) 2 , sin ω = exp(iω) ? exp(?iω) 2i ひとつの三角関数=波は, 正負の周波数をもつ指数関数の組で表される i2 = ? 1 虚数単位 「周波数がマイナス」というのはヘンだが, プラスの周波数とマイナスの周波数のペアでひとつの波になる exp(x) = ex (ex )′ = ex 微分しても変わらない e = 2.71828...
- 7. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期関数を指数関数の和で 7 周期 L の周期関数 f(x) は,波長 L / n の波を足し合わせて はず。 波長 L / n の波は f(x) = ∞ n=?∞ an exp i2π n L x と書ける exp(i2π n L x) exp(?i2π n L x) と の組 プラスもマイナスも∞
- 8. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 書ける,のはいいが 8 周期 L の周期関数 f(x) は,波長 L / n の波を足し合わせて はず。 f(x) = ∞ n=?∞ an exp i2π n L x と書ける
- 9. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 書ける,のはいいが 8 この係数はどうやって求めるの? 周期 L の周期関数 f(x) は,波長 L / n の波を足し合わせて はず。 f(x) = ∞ n=?∞ an exp i2π n L x と書ける
- 10. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 ある波長の波を切り出す 9 一方,f(x) を構成する指数関数のいずれか(波長 L / m)は exp i2π m L x 波長 L / n の指数関数 exp i2π n L x f(x) = ∞ n=?∞ an exp i2π n L x から,波長 L / nの波に 対応する指数関数だけを切り出したい
- 11. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 ある波長の波を切り出す 10 L 2 ?L 2 exp i2π m L x exp ?i2π n L x dx 波長 L / m の指数関数と L / n の指数関数についてこういう計算をしてみる
- 12. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 ある波長の波を切り出す 10 L 2 ?L 2 exp i2π m L x exp ?i2π n L x dx 波長 L / m の指数関数と L / n の指数関数についてこういう計算をしてみる 波長 L / m 波長 L / n
- 13. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 ある波長の波を切り出す 10 L 2 ?L 2 exp i2π m L x exp ?i2π n L x dx 波長 L / m の指数関数と L / n の指数関数についてこういう計算をしてみる 波長 L / m 波長 L / n f(x) の1周期分だけ積分(積分については後半で)
- 14. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 ある波長の波を切り出す 10 L 2 ?L 2 exp i2π m L x exp ?i2π n L x dx 波長 L / m の指数関数と L / n の指数関数についてこういう計算をしてみる 波長 L / m 波長 L / n f(x) の1周期分だけ積分(積分については後半で) 複素共役
- 15. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 ある波長の波を切り出す 10 L 2 ?L 2 exp i2π m L x exp ?i2π n L x dx この答は 波長 L / m の指数関数と L / n の指数関数についてこういう計算をしてみる 波長 L / m 波長 L / n f(x) の1周期分だけ積分(積分については後半で) 複素共役
- 16. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 ある波長の波を切り出す 10 L 2 ?L 2 exp i2π m L x exp ?i2π n L x dx この答は 波長 L / m の指数関数と L / n の指数関数についてこういう計算をしてみる 波長 L / m 波長 L / n f(x) の1周期分だけ積分(積分については後半で) 複素共役 mとn が異なるとき(別の波長) 0 mとn が等しいとき(同じ波長) L
- 17. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 ある波長の波を切り出す 10 L 2 ?L 2 exp i2π m L x exp ?i2π n L x dx この答は 波長 L / m の指数関数と L / n の指数関数についてこういう計算をしてみる 波長 L / m 波長 L / n f(x) の1周期分だけ積分(積分については後半で) 複素共役 mとn が異なるとき(別の波長) 0 mとn が等しいとき(同じ波長) L 指数関数はこの性質をもつ 直交関数系
- 18. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 そこで 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる
- 19. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 そこで 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる ある整数
- 20. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 そこで 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる ある整数
- 21. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 そこで 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる f(x) = ∞ n=?∞ an exp i2π n L x なので ある整数
- 22. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 そこで 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる f(x) = ∞ n=?∞ an exp i2π n L x なので ある整数
- 23. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 そこで 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる f(x) = ∞ n=?∞ an exp i2π n L x なので 1 L L 2 ?L 2 ∞ n=?∞ an exp i2π n L x exp ?i2π k L x dx ある整数
- 24. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 級数の各項を積分すると,n = k の項だけは積分すると L そこで 他の項は積分すると 0 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる f(x) = ∞ n=?∞ an exp i2π n L x なので 1 L L 2 ?L 2 ∞ n=?∞ an exp i2π n L x exp ?i2π k L x dx ある整数
- 25. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 級数の各項を積分すると,n = k の項だけは積分すると L そこで 他の項は積分すると 0 つまりこの積分の答は 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる f(x) = ∞ n=?∞ an exp i2π n L x なので 1 L L 2 ?L 2 ∞ n=?∞ an exp i2π n L x exp ?i2π k L x dx ある整数
- 26. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 級数の各項を積分すると,n = k の項だけは積分すると L そこで 他の項は積分すると 0 つまりこの積分の答は 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる f(x) = ∞ n=?∞ an exp i2π n L x なので 1 L L 2 ?L 2 ∞ n=?∞ an exp i2π n L x exp ?i2π k L x dx ある整数 1 L · Lak = ak
- 27. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ級数展開とフーリエ係数 11 級数の各項を積分すると,n = k の項だけは積分すると L そこで 他の項は積分すると 0 つまりこの積分の答は 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx を計算してみる f(x) = ∞ n=?∞ an exp i2π n L x なので 1 L L 2 ?L 2 ∞ n=?∞ an exp i2π n L x exp ?i2π k L x dx ある整数 1 L · Lak = ak 係数が求まった
- 28. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 まとめ?フーリエ級数展開とフーリエ係数 12 周期 L の周期関数 f(x) は, f(x) = ∞ n=?∞ an exp i2π n L x という波の足し合わせ(級数)で表される(フーリエ級数展開) 係数 an(フーリエ係数)は an = という積分で表される 1 L L 2 ? L 2 f(x) exp ?i2π n L x dx
- 29. 13 フーリエ変換??
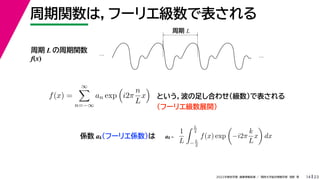
- 30. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期関数は,フーリエ級数で表される 14 周期 L の周期関数 f(x) … … f(x) = ∞ n=?∞ an exp i2π n L x という,波の足し合わせ(級数)で表される (フーリエ級数展開) 係数 ak(フーリエ係数)は 1 L L 2 ?L 2 f(x) exp ?i2π k L x dx ak = 周期 L
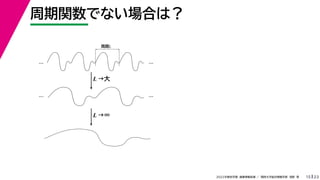
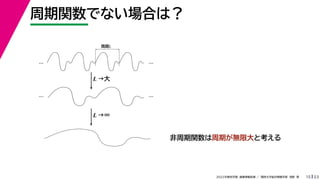
- 33. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期関数でない場合は? 15 … … 周期L … … L →大 L →∞
- 35. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L
- 36. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L 間隔1/L は周波数の差 これをΔν で表す
- 37. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L 間隔1/L は周波数の差 これをΔν で表す = Δν
- 38. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L L →大 間隔1/L は周波数の差 これをΔν で表す = Δν
- 39. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L L →大 間隔1/L は周波数の差 これをΔν で表す 1/L = Δν→小 = Δν
- 40. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L L →大 1/L 2/L 0 3/L 4/L … 間隔1/L は周波数の差 これをΔν で表す 1/L = Δν→小 = Δν Δν
- 41. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L L →大 L→∞ 1/L 2/L 0 3/L 4/L … 間隔1/L は周波数の差 これをΔν で表す 1/L = Δν→小 = Δν Δν
- 42. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L L →大 L→∞ 1/L 2/L 0 3/L 4/L … 間隔1/L は周波数の差 これをΔν で表す 1/L = Δν→0 1/L = Δν→小 = Δν Δν
- 43. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L L →大 L→∞ 1/L 2/L 0 3/L 4/L … … 間隔1/L は周波数の差 これをΔν で表す 1/L = Δν→0 1/L = Δν→小 = Δν Δν Δν ?
- 44. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L L →大 L→∞ 1/L 2/L 0 3/L 4/L … … 間隔1/L は周波数の差 これをΔν で表す フーリエ係数が隙間なく並ぶ 1/L = Δν→0 1/L = Δν→小 = Δν Δν Δν ?
- 45. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 周期 L が大きくなっていくと 16 フーリエ係数 周波数(1/波長) 1/L 2/L 0 3/L 4/L … 間隔1/L L →大 L→∞ 1/L 2/L 0 3/L 4/L … … 間隔1/L は周波数の差 これをΔν で表す フーリエ係数が隙間なく並ぶ 1/L = Δν→0 もはや足し算はできない 1/L = Δν→小 = Δν Δν Δν ?
- 46. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 17 周期 L の周期関数 f(x) は, f(x) = ∞ n=?∞ an exp i2π n L x
- 47. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 17 周期 L の周期関数 f(x) は, f(x) = ∞ n=?∞ an exp i2π n L x an = 1 L L 2 ? L 2 f(x) exp ?i2π n L x dx
- 48. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 17 周期 L の周期関数 f(x) は, f(x) = ∞ n=?∞ an exp i2π n L x an = 1 L L 2 ? L 2 f(x) exp ?i2π n L x dx 1/L =Δν と書き換える
- 49. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 17 周期 L の周期関数 f(x) は, f(x) = ∞ n=?∞ an exp i2π n L x an = 1 L L 2 ? L 2 f(x) exp ?i2π n L x dx 1/L =Δν と書き換える f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx)
- 50. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 17 周期 L の周期関数 f(x) は, f(x) = ∞ n=?∞ an exp i2π n L x an = 1 L L 2 ? L 2 f(x) exp ?i2π n L x dx 1/L =Δν と書き換える f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) 紛らわしいので別の文字にしただけ
- 51. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 18 nΔν はある周波数を表すので,ν であらわす L→∞ のとき Δν→0 f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) という積分になる このとき のなかの総和(Σ)が, f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν
- 52. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 18 nΔν はある周波数を表すので,ν であらわす L→∞ のとき Δν→0 f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) という積分になる このとき のなかの総和(Σ)が, f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν
- 53. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 18 nΔν はある周波数を表すので,ν であらわす L→∞ のとき Δν→0 f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) という積分になる このとき のなかの総和(Σ)が, f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν ?????
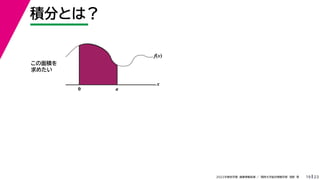
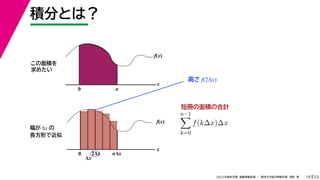
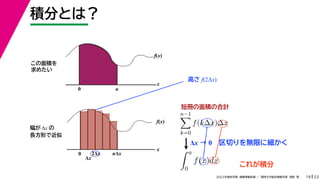
- 55. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい f(x) x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 0 a
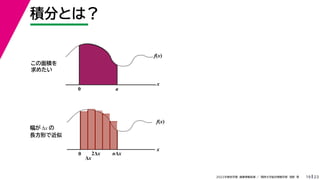
- 56. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい f(x) x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 0 a
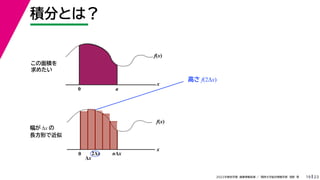
- 57. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい f(x) x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 高さ f(2Δx) 0 a
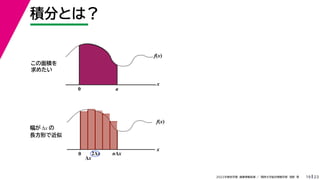
- 58. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい f(x) x n?1 k=0 f(k?x)?x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 高さ f(2Δx) 0 a 短冊の面積の合計
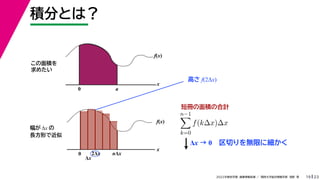
- 59. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい Δx → 0 区切りを無限に細かく f(x) x n?1 k=0 f(k?x)?x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 高さ f(2Δx) 0 a 短冊の面積の合計
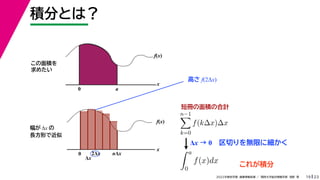
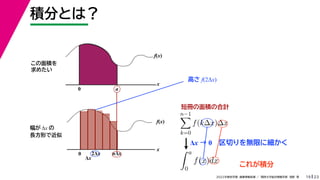
- 60. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい Δx → 0 区切りを無限に細かく f(x) x n?1 k=0 f(k?x)?x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 高さ f(2Δx) 0 a a 0 f(x)dx これが積分 短冊の面積の合計
- 61. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい Δx → 0 区切りを無限に細かく f(x) x n?1 k=0 f(k?x)?x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 高さ f(2Δx) 0 a a 0 f(x)dx これが積分 短冊の面積の合計
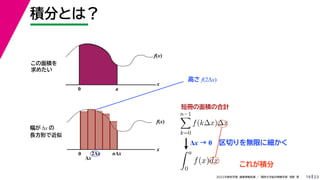
- 62. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい Δx → 0 区切りを無限に細かく f(x) x n?1 k=0 f(k?x)?x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 高さ f(2Δx) 0 a a 0 f(x)dx これが積分 短冊の面積の合計
- 63. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 積分とは? 19 この面積を 求めたい Δx → 0 区切りを無限に細かく f(x) x n?1 k=0 f(k?x)?x f(x) x 0 Δx 2Δx nΔx 幅が Δx の 長方形で近似 高さ f(2Δx) 0 a a 0 f(x)dx これが積分 短冊の面積の合計
- 64. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 20 nΔν はある周波数を表すので,ν であらわす L→∞ のとき Δν→0 f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) という積分になる このとき のなかの総和(Σ)が, f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν Δx → 0 区切りを無限に細かく n?1 k=0 f(k?x)?x a 0 f(x)dx
- 65. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 20 nΔν はある周波数を表すので,ν であらわす L→∞ のとき Δν→0 f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) という積分になる このとき のなかの総和(Σ)が, f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν Δx → 0 区切りを無限に細かく n?1 k=0 f(k?x)?x a 0 f(x)dx
- 66. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 20 nΔν はある周波数を表すので,ν であらわす L→∞ のとき Δν→0 f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) という積分になる このとき のなかの総和(Σ)が, f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν Δx → 0 区切りを無限に細かく n?1 k=0 f(k?x)?x a 0 f(x)dx
- 67. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 20 nΔν はある周波数を表すので,ν であらわす L→∞ のとき Δν→0 f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) という積分になる このとき のなかの総和(Σ)が, f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν Δx → 0 区切りを無限に細かく n?1 k=0 f(k?x)?x a 0 f(x)dx
- 68. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 級数から積分へ 20 nΔν はある周波数を表すので,ν であらわす L→∞ のとき Δν→0 f(x) = ∞ n=?∞ ?ν L 2 ?L 2 f(τ) exp (?i2πn?ντ) dτ exp (i2πn?νx) という積分になる このとき のなかの総和(Σ)が, f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν !!! Δx → 0 区切りを無限に細かく n?1 k=0 f(k?x)?x a 0 f(x)dx
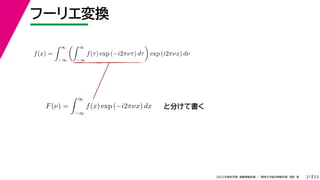
- 69. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ変換 21 f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν
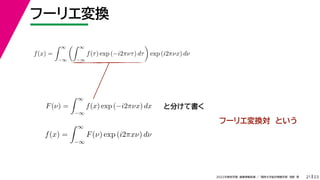
- 70. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ変換 21 f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν F(ν) = ∞ ?∞ f(x) exp (?i2πνx) dx と分けて書く
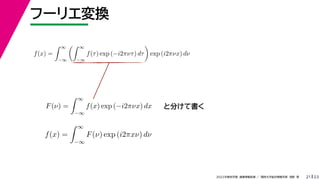
- 71. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ変換 21 f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν F(ν) = ∞ ?∞ f(x) exp (?i2πνx) dx f(x) = ∞ ?∞ F(ν) exp (i2πxν) dν と分けて書く
- 72. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ変換 21 f(x) = ∞ ?∞ ∞ ?∞ f(τ) exp (?i2πντ) dτ exp (i2πνx) dν F(ν) = ∞ ?∞ f(x) exp (?i2πνx) dx f(x) = ∞ ?∞ F(ν) exp (i2πxν) dν と分けて書く フーリエ変換対 という
- 73. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ変換 22 F(ν) = ∞ ?∞ f(x) exp (?i2πνx) dx f(x) = ∞ ?∞ F(ν) exp (i2πxν) dν フーリエ変換 逆フーリエ変換
- 74. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ変換 22 F(ν) = ∞ ?∞ f(x) exp (?i2πνx) dx f(x) = ∞ ?∞ F(ν) exp (i2πxν) dν フーリエ変換 関数 f(x) にどのような周波数の波がどれだけ含まれているか,「波を切り出す」 逆フーリエ変換
- 75. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ変換 22 F(ν) = ∞ ?∞ f(x) exp (?i2πνx) dx f(x) = ∞ ?∞ F(ν) exp (i2πxν) dν フーリエ変換 関数 f(x) にどのような周波数の波がどれだけ含まれているか,「波を切り出す」 逆フーリエ変換 フーリエ係数の並びだったのが,周波数の間隔がどんどん小さくなって, ついにはひとつの関数 F(ν) になる
- 76. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 フーリエ変換 22 F(ν) = ∞ ?∞ f(x) exp (?i2πνx) dx f(x) = ∞ ?∞ F(ν) exp (i2πxν) dν フーリエ変換 関数 f(x) にどのような周波数の波がどれだけ含まれているか,「波を切り出す」 逆フーリエ変換 フーリエ係数の並びだったのが,周波数の間隔がどんどん小さくなって, ついにはひとつの関数 F(ν) になる 周波数 ν の波 exp(i2πxν) に,対応するフーリエ係数 F(ν) をかけたものを 合計(積分)すると f(x) に戻る
- 77. 23 2022年度秋学期 画像情報処理 / 関西大学総合情報学部 浅野 晃 2次元の場合は 23 F(ν) = ∞ ?∞ f(x) exp (?i2πνx) dx 1次元のフーリエ変換 この式は,x, y それぞれに1次元のフーリエ変換をしたことになっている 2次元のフーリエ変換 F(νx, νy) = ∞ ?∞ f(x, y) exp{?i2π(νxx + νyy)}dxdy F(νx, νy) = ∞ ?∞ ∞ ?∞ f(x, y) exp(?i2πνxx)dx exp(?i2πνyy)dy exp(a + b) = exp(a) exp(b) 注: 足し算 かけ算