Een touwtje om de aarde
- 1. Een paar vragen Antwoorden Uitwerkingen Een touwtje om de aarde Quidquid latine dictum sit, altum videtur K. P. Hart Faculty EEMCS TU Delft Leiden, 22 oktober 2014: 13:00 13:45 K. P. Hart Een touwtje om de aarde
- 2. Een paar vragen Antwoorden Uitwerkingen Vraag 1 Stel je voor dat er een touw strak om de aarde getrokken is, zeg over de polen. Maak het touw 卒e卒en meter langer en til het overal even hoog op. Hoe hoog komt het touw boven het aardoppervlak? K. P. Hart Een touwtje om de aarde
- 3. Een paar vragen Antwoorden Uitwerkingen Vraag 2 Stel je voor dat er een touw strak om de aarde getrokken is, zeg over de polen. Maak het touw 卒e卒en meter langer en til bij de Noordpool op, tot het strak staat. (Alsof je de aarde met het touw aan een spijker hangt.) Hoe hoog is die spijker boven de Noordpool? K. P. Hart Een touwtje om de aarde
- 4. Een paar vragen Antwoorden Uitwerkingen Vraag 3 Boor een kaarsrechte tunnel van (De Dam in) Amsterdam naar de Martinitoren in Groningen. Hoe diep ligt de tunnel halverwege? Tussen de 卒e卒en en tien meter? Tussen de tien en honderd meter? Tussen de honderd en duizend meter? K. P. Hart Een touwtje om de aarde
- 5. Een paar vragen Antwoorden Uitwerkingen Antwoord 1 Vraag 1 is een bekend raadseltje en het antwoord is onafhankelijk van de straal, R, van de aarde. We zoeken h z卒o dat 2R + 1 = 2(R + h). Oplossing: h = 1 2 (ongeveer 16 cm). K. P. Hart Een touwtje om de aarde
- 6. Een paar vragen Antwoorden Uitwerkingen Antwoord 2 Vraag 2 is wat minder bekend. Het verhaal stond in November 2004 in Pythagoras en het was vraag 4 van de Nationale Wetenschapsquiz 2010 Het was in december 2010 heel druk op http://dutiaw37.twi.tudelft.nl/~kp/stukjes-pythagoras/jg44/2004-11/ Antwoord: ongeveer 120 m K. P. Hart Een touwtje om de aarde
- 7. Een paar vragen Antwoorden Uitwerkingen Antwoord 3 Dit was ooit een kwisvraagje dat voor Pythagoras gemaakt was, vandaar de drie keuzemogelijkheden. Antwoord: tussen honderd en duizend meter (wat meer dan 400 m). Hoe doe je zoiets snel, op een kladje, zonder rekenmachientje? K. P. Hart Een touwtje om de aarde
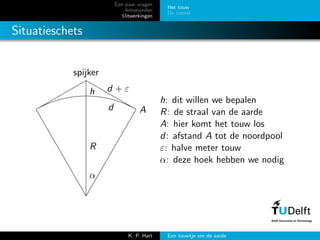
- 8. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Situatieschets spijker h R Ad d + 竜 留 h: dit willen we bepalen R: de straal van de aarde A: hier komt het touw los d: afstand A tot de noordpool 竜: halve meter touw 留: deze hoek hebben we nodig K. P. Hart Een touwtje om de aarde
- 9. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Betrekkingen d = 留 揃 R (of 留 = d/R) en (R + h)2 = R2 + (d + 竜)2 (Pythagoras) Dus h = R2 + (d + 竜)2 R = R 1 + 留 + 竜 R 2 1 Om h te bepalen hebben we R en 留 nodig. K. P. Hart Een touwtje om de aarde
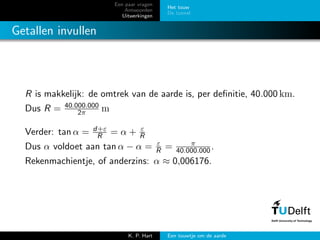
- 10. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Getallen invullen R is makkelijk: de omtrek van de aarde is, per de鍖nitie, 40.000 km. Dus R = 40.000.000 2 m Verder: tan 留 = d+竜 R = 留 + 竜 R Dus 留 voldoet aan tan 留 留 = 竜 R = 40.000.000. Rekenmachientje, of anderzins: 留 0,006176. K. P. Hart Een touwtje om de aarde
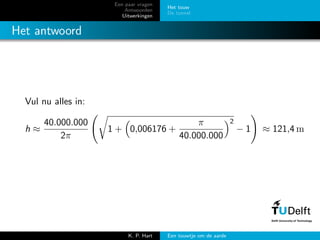
- 11. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Het antwoord Vul nu alles in: h 40.000.000 2 1 + 0,006176 + 40.000.000 2 1 121,4 m K. P. Hart Een touwtje om de aarde
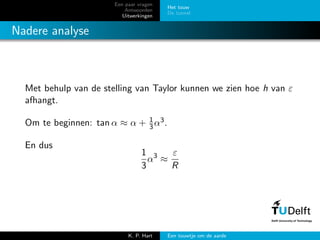
- 12. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Nadere analyse Met behulp van de stelling van Taylor kunnen we zien hoe h van 竜 afhangt. Om te beginnen: tan 留 留 + 1 3留3. En dus 1 3 留3 竜 R K. P. Hart Een touwtje om de aarde
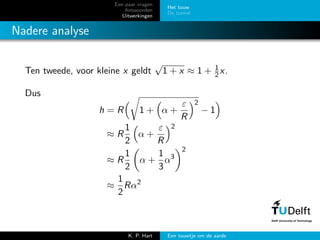
- 13. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Nadere analyse Ten tweede, voor kleine x geldt 1 + x 1 + 1 2x. Dus h = R 1 + 留 + 竜 R 2 1 R 1 2 留 + 竜 R 2 R 1 2 留 + 1 3 留3 2 1 2 R留2 K. P. Hart Een touwtje om de aarde
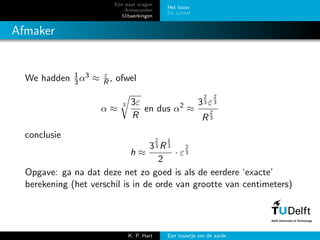
- 14. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Afmaker We hadden 1 3留3 竜 R , ofwel 留 3 3竜 R en dus 留2 3 2 3 竜 2 3 R 2 3 conclusie h 3 2 3 R 1 3 2 揃 竜 2 3 Opgave: ga na dat deze net zo goed is als de eerdere exacte berekening (het verschil is in de orde van grootte van centimeters) K. P. Hart Een touwtje om de aarde
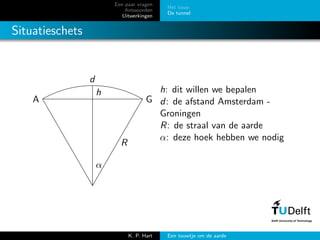
- 15. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Situatieschets A G h d R 留 h: dit willen we bepalen d: de afstand Amsterdam - Groningen R: de straal van de aarde 留: deze hoek hebben we nodig K. P. Hart Een touwtje om de aarde
- 16. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Betrekkingen De formule voor h is redelijk eenvoudig: h = R(1 cos 留) De situatie: een diner Beschikbaar materiaal: servetjes en pennen Geen rekenmachientjes, e.d. (dit was lang geleden) K. P. Hart Een touwtje om de aarde
- 17. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel De schatting Met de natte vinger: d ligt tussen de 100 en 200 kilometer. Dus, met 留 = d 2R , 400 留 200 Dus 留 is vrij klein. In dat geval sin 留 留 en cos 留 = 1 = 2 sin2 1 2留 1 1 2留2, we benaderen h met h 1 2 R留2 K. P. Hart Een touwtje om de aarde
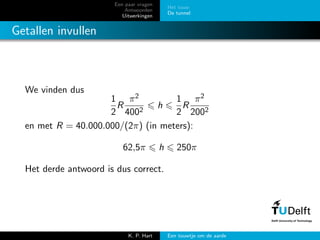
- 18. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Getallen invullen We vinden dus 1 2 R 2 4002 h 1 2 R 2 2002 en met R = 40.000.000/(2) (in meters): 62,5 h 250 Het derde antwoord is dus correct. K. P. Hart Een touwtje om de aarde
- 19. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Nauwkeurigheid De afstand Amsterdam-Groningen is ongeveer 150 km. Met de benadering vinden we h 441,79 m. Hoe betrouwbaar is dit eigenlijk? K. P. Hart Een touwtje om de aarde
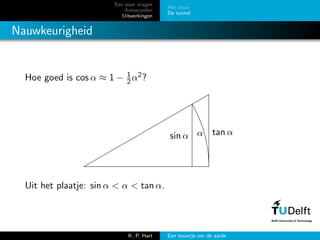
- 20. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Nauwkeurigheid Hoe goed is cos 留 1 1 2留2? sin 留 留 tan 留 Uit het plaatje: sin 留 < 留 < tan 留. K. P. Hart Een touwtje om de aarde
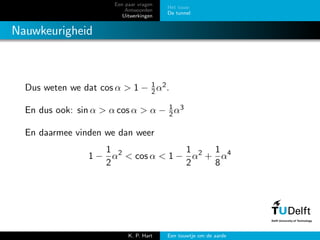
- 21. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Nauwkeurigheid Dus weten we dat cos 留 > 1 1 2留2. En dus ook: sin 留 > 留 cos 留 > 留 1 2留3 En daarmee vinden we dan weer 1 1 2 留2 < cos 留 < 1 1 2 留2 + 1 8 留4 K. P. Hart Een touwtje om de aarde
- 22. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Nauwkeurigheid Gevolg van dit al: 1 2 R留2 > h > 1 2 R留2 1 8 R留4 Met d = 150 km vinden we 1 8 R留4 1,5 cm Moraal: de fout door de benadering is te verwaarlozen K. P. Hart Een touwtje om de aarde
- 23. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Taylor De getallen 1 2 en 1 8 de ongelijkheden voor sin 留 en cos 留 zijn niet optimaal, de stelling van Taylor geeft ons sin 留 = 留 1 6 留3 + 1 120 留5 + 揃 揃 揃 en cos 留 = 1 1 2 留2 + 1 24 留4 1 720 留6 + 揃 揃 揃 Zie de Analyse (en Wiskundige Structuren). K. P. Hart Een touwtje om de aarde
- 24. Een paar vragen Antwoorden Uitwerkingen Het touw De tunnel Verder lezen? Op www.pyth.eu Tunnel: April 2001, en Touw: November 2004 Of op fa.its.tudelft.nl/hart (Volg link naar Pythagoras.) K. P. Hart Een touwtje om de aarde