狠狠撸

2013年9月21日
曲面の微分幾何学
ring

講演の目的
? Gauss曲率の幾何学的な意味を理解し,微分形
式を使って計算できるようになる.
? 離散Gauss-Bonnetの定理の紹介.
– 余裕があれば.

講演内容
1. Gaussian frameを用いる方法
2. Moving frameを用いる方法…◎
3. 離散Gauss-Bonnetの定理

1 Gaussian frameを用いる方法

手順
1. 第一基本量E, F, Gを計算する.
2. 第二基本量L, M, N を計算する.
3. 第一,第二基本量からGauss曲率K を計算する.
K =
LN ? M2
EG ? F2

曲面の表示
曲面のパラメータ表示
p : R2
→ R3
p(u, v) =
?
?
x(u, v)
y(u, v)
z(u, v)
?
?
pu, pv は一次独立とする. → 接平面の基底.

Gaussian frame
e :=
pu × pv
|pu × pv|
{pu, pv, e}： Gaussian frame → R3
の基底.

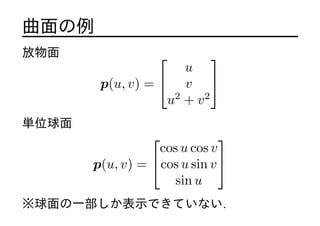
曲面の例
放物面
p(u, v) =
?
?
u
v
u2
+ v2
?
?
単位球面
p(u, v) =
?
?
cos u cos v
cos u sin v
sin u
?
?
※球面の一部しか表示できていない.

第一基本量
E := pu · pu
F := pu · pv = pv · pu
G := pv · pv
MI :=
[
E F
F G
]
※ MI：pu, pv のGram行列.

接ベクトルの長さ
接ベクトル ξ = apu + bpv の長さの二乗は
I(ξ) :=
[
a b
]
MI
[
a
b
]
で与えられる.i.e.
|ξ|2
= I(ξ)

第二基本量
L := puu · e
M := puv · e = pvu · e
N := pvv · e
MII :=
[
L M
M N
]

接ベクトル方向への曲率
接ベクトル ξ = apu + bpv 方向への曲率は
II(ξ) :=
[
a b
]
MII
[
a
b
]
で与えられる（e 方向を正とする.）

主曲率
? 曲率が最も大きく（小さく）なる方向は？
– 条件 I(ξ) = 1 の下での II(ξ) の極値問題.
? 最大値,最小値κ1, κ2 を主曲率という.

Gauss曲率
Gauss曲率 K := κ1κ2
K =
LN ? M2
EG ? F2
= det
(
MIIM?1
I
)
※ K の符号で曲面の形がわかる.

例（トーラス）１
トーラスのパラメータ表示
p(u, v) =
?
?
(R + r cos u) cos v
(R + r cos u) sin v
r sin u
?
?
E = r2
F = 0 G = (R + r cos u)2
L = r M = 0 N = (R + r cos u) cos u

例（トーラス）２
トーラスのGauss曲率
K =
cos u
r(R + r cos u)
K(0) > 0
K(π/2) = 0
K(π) < 0

2 Moving frame を使う方法

手順
1. 接平面の正規直交基底 e1, e2 をとる.
2. 双対基底 θ1, θ2 を微分して接続形式を求める.
– 第一構造方程式.
3. 接続形式ω1
2 を微分してGauss曲率K を求める.
– 第二構造方程式.

微分形式１
? 0-form（関数）
f(u, v)
? 1-form
f(u, v)du + g(u, v)dv
? 2-form
f(u, v)du ∧ dv

微分形式２
Wedge 積
ω：k-form, η：l-form ? ω ∧ η：(k + l)-form
η ∧ ω = (?1)kl
ω ∧ η
特に, du ∧ du = dv ∧ dv = 0.

微分形式３
外微分d ※ d2
= 0
? 0-form
df := fudu + fvdv
? 1-form
d(fdu + gdv) = (gu ? fv)du ∧ dv
? 2-form
d(fdu ∧ dv) = 0

微分形式４
Wedge積の外微分
ω：k-form, η：l-form
d(ω ∧ η) = dω ∧ η + (?1)k
ω ∧ dη
※ l に依らない.

Moving frame
{e1, e2}：接平面の正規直交基底, e3 := e
{e1, e2, e3}： moving frame
[
pu pv
]
=
[
e1 e2
]
A
※ det A > 0 とする.

双対基底
[
θ1
θ2
]
:= A
[
du
dv
]
dp = e1θ1
+ e2θ2

第一構造方程式
dθ1
= ?ω1
2 ∧ θ2
dθ2
= ?ω2
1 ∧ θ1
※ ω2
1 = ?ω1
2：接続形式

第二構造方程式
dω1
2 = Kθ1
∧ θ2
※ K：Gauss曲率

例（トーラス）
p(u, v) =
?
?
(R + r cos u) cos v
(R + r cos u) sin v
r sin u
?
?
[
θ1
θ2
]
=
[
rdu
(R + r cos u)dv
]
ω1
2 = sin udv
K =
cos u
r(R + r cos u)

例（球）
p(u, v) =
?
?
r cos u cos v
r cos u sin v
r sin u
?
?
[
θ1
θ2
]
=
[
rdu
r cos udv
]
ω1
2 = sin udv
K =
1
r2

例（カテノイド）
p(u, v) =
?
?
u cos v
u sin v
cosh?1
u
?
?
[
θ1
θ2
]
=
[
udu/
√
u2 ? 1
udv
]
ω1
2 = ?
√
u2 ? 1dv/u
K = ?1/u4

例（擬球）
p(u, v) =
?
?
e?u
cos v
e?u
sin v∫ u
0
√
1 ? e?2tdt
?
?
[
θ1
θ2
]
=
[
du
e?u
dv
]
ω1
2 = e?u
dv
K = ?1

狠狠撸

20130921冲曲面の微分几何学

Recommended

More Related Content

What's hot (20)

Similar to 20130921冲曲面の微分几何学 (8)

More from matsumoring (7)

20130921冲曲面の微分几何学