H7 blm221 (1)
- 1. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM 221 MANTIK DEVRELERİ Prof Dr Mehmet AKBABA mehmetakbaba@karabuk.edu.tr 7. HAFTA
- 2. Temel Kavramlar KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 2 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI • Dört basamaklı (Düzeyli) Mantık Devresi • Üç basamaklı (Düzeyli) Mantık Devresi • NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları • Ġki ve Üç Basamaklı (Düzeyli) NAND VE NOR Kapısı Devrelerinin Tasarımı • Çok basamaklı (düzeyli) NAND ve NOR Kapıları Devreleri • Alternatif Simge Kullanarak Devre DönüĢümü • Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı • Çok çıkıĢlı NOR ve NAND kapısı devreleri
- 3. ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 3 ġekil 7.1: Dört basamaklı (Düzeyli) Mantık Devresi
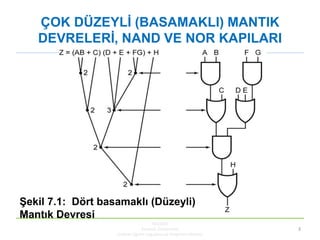
- 4. ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 4 Z’ nin ifadesini baĢka türlü yazarak üç basamaklı devre elde edebiliriz. Bu kısmi çarpma ile gerçekleĢtirilebilir. Z= (AB + C)[(D + E) + FG ] + H = AB(D + E) + C(D + E) + ABFG + CFG + H
- 5. ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 5 Şekil 7.2: Üç basamaklı (Düzeyli) Mantık Devresi
- 6. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 6 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI Problem: AĢağıda verilen lojik fonksiyonu AND ve OR kullanarak gerçekleĢtiriniz: f(a,b,c,d) =  m(1,5,6,10,13,14) Kuaracağınız devreyi iki basamaklı (düzeyli) ve üç düzeyli olarak tasarlayınız. Her iki devreden hangisinin daha basit ve en az lojik kapı kullanılarak gerçekleĢtirildiğini belirleyiniz ve sonucun yorumunu yapınız. Bütün değiĢkenlerin kendilerinin ve tümleyenlerinin giriĢ olarak hazır olduğunu varsayın.
- 7. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 7 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI ġekil 7.3 (7.1)
- 8. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 8 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI Şekil 7.4 f=a’b’c+bc’d+bcd+acd’ Bu eĢitliği gerçekleĢtiren devre aĢağıda verilmiĢtir Ġki basamaklı (düzeyli), beĢ kapılı, 16 kapı giriĢli devre
- 9. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 9 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI (7.1) eĢitliğinde ortak terimler kullanılırsa aynı fonksiyon aĢağıdaki yazılabilir: F=c’d(a’+b)+cd’(a+b) (7.2) (buda üç basamaklı bir devreye dönüĢür) Üç basamaklı (seviyeli) beĢ kapılı 12 kapı giriĢli devreġekil 7.5
- 10. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 10 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI Karno haritasında sıfırlar kullanılarak aynı fonksiyonun Tersi aĢağıdaki Ģekilde elde edilir: f’= c’ d’ + ab’ c’ + cd + a’ b’ c (7.3) (7.3) ün tersi alınırsa: f = (c + d)( a’ + b + c )(c’ +d’ )( a + b + c’ ) (7.4) Elde edilir. (7.4) EĢitliği iki seviyeli OR-AND devresi ile ġekil 7.6 daki gibi gerçekleĢtirilebilir.
- 11. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 11 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI Üç basamaklı (seviyeli) beĢ kapılı 12 kapı giriĢli devre ġekil 7.6
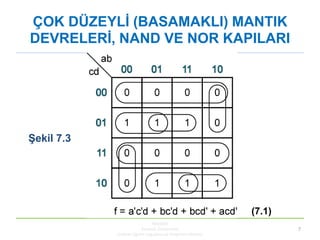
- 12. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 12 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI Üç basamaklı AND çıkıĢlı devre elde edebilmek için (7.4) denklemine önce (X+Y)(X+Z)=X+YZ teoremi uygulayalım: f = [c + d(a’ + b )][c’ + d’ (a+b)] (7.5) elde edilir. (7.5) eĢitliği dört basamaklı devre gerektirir. KöĢeli parantez içindeki ifadeleri çarpıp açarsak : f = (c + a’ d + bd )(c’ + ad’ +bd’ ) (7.6) elde edilir. (7.6) eĢitliği üç basamaklı AND-OR-AND devresi olarak ġekil 7.7 verildiği gibi gerçekleĢtirilir:
- 13. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 13 ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK DEVRELERĠ, NAND VE NOR KAPILARI Üç basamaklı (seviyeli) yedi kapılı 16 kapı giriĢli devre ġekil 7.7
- 14. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 14 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları Buraya kadar lojik ifadeleri AND, OR ve EX-OR kapıları ile gerçekleĢtirdik. Bu bölümde NAND ve NOR kapıları tanıtılacak ve devrelerin bu kapılarla nasıl gerçekleĢtirileceği gösterilecektir. NAND ve NOR kapıları daha hızlı çalıĢtıklarından ve genel olarak daha az devre elemanı kullanılarak yapıldıklarından lojik devre tasarımcılarının çokça tercih edilmektedirler.
- 15. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 15 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları 2.1 NAND Kapısı ġekil 7.8(a) da NAND kapısının simgesi gösterilmiĢtir. VE (AND) kapısının çıkıĢ ucuna küçük bir daire eklenince NAND kapısı simgesi elde edilir. ÇıkıĢ ucundaki küçük daire ters alma alma veya tümleyan alma veya değilleme (NOT) anlamında kullanılmaktadır. NADN kapısı ġekil 7.8(b) de görildüğü gibi AND kapısının sonuna bir NOT (ters alma) kapısı eklenerek elde edilebilir. Buda NAND kapısının AND kapısının terine eĢit olduğu anlamina gelir veya NADN=AND.NOT= (AND)’ yazılabilir. NAND kapısının bağıntısı aĢağıdaki gibidir: F=(ABC)’=A’+B’+’C’ Görüldüğü gibi NAND kapısı giriĢ değiĢkenlerinin terslerini toplayan bir devredir.
- 16. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 16 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları n giriĢli bir NAND kapısının çıkıĢ bağıntısı F=(X1X2X3……….Xn)’=X1’+X2’+X3’+……..Xn’ (7.8) (7.8) bağıntısı NAND kapısının giriĢlerinden en az birisi 0 ise kapının çıkiĢ değiĢkeninin 1 olması gerektiğini ifade etmaktedir.
- 17. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 17 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları NAND kapısı NAND  AND-NOT =(AND)’ (ABC)’=A’+B’+C’ (değillerin (terslerin) toplamı (a) Üç kapılı NAND kapısı (b) NAND eĢdeğer devresi (c) n giriĢli NAND Şekil 7.8: NAND kapısı (gate)
- 18. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 18 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları 2.2 NOR Kapısı ġekil 7.9(a) üç giriĢli NOR kapısını göstermektedir. Simgenin çıkıĢındaki küçük daire iĢareti tersleme (NOT veya tümleyen) anlamında kullanılmaktadır. Bu nedenle NOR kapısı OR kapısını izleyen bir NOT kapısının bileĢiminden oluĢmaktadır. NOR=OR.NOT=(OR)’ Üç giriĢli bir NOR kapısının çıkıĢ değiĢkeninin ifadesi F=(A+B+C)’=A’B’C’ (terslerin (tümleyenlerin) çarpımı) olur.
- 19. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 19 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları NOR gate NOR kapısı ≡ NOR-NOT =(NOR)’ (A+B+C)’=A’B’C’ (tümleyenlerin çarpımları) (a) Üç kapılı NOR kapısı (b) NOR eĢdeğer devresi (c) n giriĢli NOR Şekil 7.9: NOR kapısı (gate)
- 20. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 20 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları ġekil 7/9(c) de göserilen n-giriĢli NOR (VEYA) kapsımın çıkıĢ değĢkeninin ifadesi: Figure is F = (X1+X2+………+Xn)’ = X1’ X2’……Xn’ (7.9) Herhangi bir kapı diğer kapılar kullanılarak geçekleĢtirilebilir. Örneğin VEYA kapısı NOT ve AND kapıları ile aĢağıdaki gibi gerçekleĢtirilebilir:
- 21. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 21 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları Şekil 7.10: NAND kapısının NOT, AND, ve OR kapıları ile gerçekleĢtirilmesi
- 22. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 22 NAND (VE-DEĞĠL) ve NOR (VEYA-DEĞĠL) Kapıları AND veya OR kapısı varsa, bir diğri DeMorgan kuralı kullanılarak gerçekleĢtirilebilir. Örneğin, OR ve NOT varsa, AND and aiağıdeki gibi gerçekleĢtirilir: XY = (X' + Y’)’ (7.10)
- 23. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 23 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI Ġki basamaklı (düzeyli) AND ve OR kapı vevreleri kolayca NAND ve NOR kapı devrelerine dönüĢtürülebilir. Bu dönüĢümde DeMorgan kuralı aĢağıdaki gibi kullanılır: (7.11) (7.12) AĢağıdaki örnek minimum SOP ifadesinin değiĢik diğer formlara nasıl dönüĢtürüldüğünü göstermektedir: (X1+X2+X3+...........Xn)’=X1’.X2’.X3’...............Xn’ (X1.X2.X3........Xn)’=X1’+X2’+X3’+............+Xn’
- 24. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 24 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI (7.13), (7.14), (7.15) ve (7.16) eĢitlikleri ġekil 7.11 de gösterildiği gibi, sıra ile AND-OR, NAND-NAND, OR- NAND, NOR-OR devrelerine karĢılık gelmektedirler. (7.16) eĢitliğini yeniden aĢağıdaki gibi yazalım: F = {[A + (B' + C)' + (B + C' + D')' ]'}' F = A + BC' + B‘ C D = [(A +B C‘ + B’ CD)’ ]' = [A' • (BC‘ )' • (B‘ CD)‘ ] ' = [A' • (B' + C) • (B + C' + D‘ ) ]' = A + (B' + C)' + (B + C' + D‘ )' (7.17) (7.13) (7.11) den (7.14) (7.12) den (7.15) (7.12) den (7.16)
- 25. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 25 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI (7.17) eĢitliği üç bamaklı NOR-NOR-INVERT devresi verir. Fakat iki basamaklı NOR devresi elde etmek istiyorsak, minimum SOP yerine minimum POS (product-of-sums) formu ile baĢlamamız gerekir. Karnaugh haritasından minimum POS ifadesi bulunduktan sonra fonksiyon aĢağıdaki gibi iki basamaklı devre veren formda yazılır: F=(A+B+C)(A+B’+C’)(A+C’+D) = {[(A+B+C)(A+B’+C’)(A+C’+D)]’}’ = [(A+B+C)’+(A+B’+C’)’+(A+C’+D)’]’ = (A’B’C’+A’BC+A’CD’)’ = (A’B’C’)’.(A’BC)’.(A’CD’)’ (7.18) (7.19) (7.20) (7.21)
- 26. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 26 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI Şekil 7.11(a): Ġki basamaklı (düzeyli) sekiz temel devreler (devamı ġekil 7.11(b) de)
- 27. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 27 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI F=,*(A+B+C)(A+B’+C’)(A+C’+D)+’-’ =,A’B’C’+A’BC+A’CD’-’ =(A’B’C’)’.(A’BC)’.(A’CD’)’ F=*(A+B+C)’+(A+B’+C’)’+(A+C’+D)’+’ Şekil 7.11(b): Ġki basamaklı (düzeyli) sekiz temel devreler
- 28. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 28 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI F=[(abcde’)’+’=*(ab)(cd)e’)’+’=*(ab)’+(cd)’+e+’ Bir fonksiyonun tersinin tersi kendisini verir (hatırlatma). POS Ģeklinde yazılmıĢ herhagi bir lojik fonksiyon NAND-NOR olarak gerçeleĢtirilebilir. Örnek: (F=(a+a)(b+b)(c+c)(d+d)(e’+e’) yazılıp POS şekline dönüştürülebilir)
- 29. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 29 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI İki Basamaklı NAND-NAND devresi tasarımı yapılası işlemi 1. Fonksiyonun minimum SOP ifadesini bulunuz. 2. Buna karşılık gelen iki basamaklı (düzeyli) AND-OR devresini çiziniz. 3. Sonra aynı çizizmi, arabağlantıları aynı bırakarak aynı çizizmi NAND kapıları ile tekrarlayınız. 4. Herhangi bir kapının girişinde tek literal (değişken) varsa o literalin tümleyenini alınız.
- 30. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 30 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI Şekil 7.12 AND-OR devresinden NAND devresine geçmek için yapılması gereken adımları sergilemektedir. Devrenin çıkışında herhangi bir değişiklik olmamaktadır. Genel olarak fonksiyon literallerin toplamı (l1, l2, l3,….) ve çarpım terimlerden (P1, P2,…..) oluşmaktadır. F = l1 + l2 +…..+ P1 + P2 + ….. DeMorgan kuralı uygulandıktan sonra F = (l1’ l2‘ ……… P1‘ P2’ …..)’
- 31. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 31 ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE NOR KAPISI DEVRELERĠNĠN TASARIMI Şekil 7.12: AND-OR devresinin NAND-NAND devresine dönüĢtürülmesi örneği (a) DönüĢtürülmeden önceki devre (b) DönüĢtürülmeden sonraki devre
- 32. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 32 Çok basamaklı (düzeyli) NAND ve NOR Kapıları Devreleri Örnek: AĢağıdaki fonksiyonu NAND devresi ile geçekleĢtiriniz. F1=a’ [b’ + c(d + e’ ) + f’ g’ ] + hi’ j + k ġekil 7.13 görüldüğü gibi devrenin Ģması önce AND-OR devresi olarak çizilmiĢ ve daha sonra yukarıda anlatıldığı gibi NAND devresine dönüĢtürülmüĢtür.
- 33. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 33 Çok basamaklı (düzeyli) NAND ve NOR Kapıları Devreleri (a) AND-OR devresi (b) NAND devresi ġekil 7.13 Çok basamaklı NAND devresi dönüĢümü 1. basamak2. basamak3. basamak4. basamak5. basamak 1. basamak2. basamak3. basamak4. basamak5. basamak
- 34. KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 34 Alternatif Simge Kullanarak Devre DönüĢümü Alternatif kapı Simgeleri NOT Şekil 7.14: Alternatif Kapı Simgeleri
- 35. Alternatif Simge Kullanarak Devre DönüĢümü KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 35 (a) NAND kapısı devresi (b) Alternatif NAND kapısı devresi (c) Eşdeğer AND-OR kapısı devresi Şekil 7.15: NAND Kapı devresi dönüĢümü
- 36. Alternatif Simge Kullanarak Devre DönüĢümü KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 36 (a) OR ve AND kapılarından oluşan devresi Çift terslemeler biribirini yok ediyor Tümleyeni alınmış girişler terslemeleri yok ediyor (b) NOR kapıları ile kurulmuş devre Şekil 7.16: NAND Kapı devresi dönüĢümü
- 37. Alternatif Simge Kullanarak Devre DönüĢümü KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 37 (a) AND-OR devresi Küçük dairecikler (bubbles) biribirini yok ediyor (b) NAND’e dönüştürmede ilk basamak İlave edilmiş inverter İlave edilmiş inverter Şekil 7.17: AND-OR devresinin NAND devresine dönüĢtürülmesi (c) İlaveli alternatif dönüştürme
- 38. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 38 Bu konu aĢağda verilen bir örneklerle açıklanacaktır. ÖNEK 1: AĢağıdaki üç fonksiyonu sağlayan dört giriĢli üç çıkıĢlı bir devre tasarlayalım: F1(A,B,C,D)=m(11,12,13,14,15) F2(A,B,C,D)=m(3,7,11,12,13,15) F3(A,B,C,D)=m(3,7,12,13,14,15) (7.22)
- 39. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 39 Şekil 7.18: (7.22) EĢtliklerini minimize eden Karnaugh haritası F1=AB+ACD F2=CD+ABC’ F3=AB+A’CD
- 40. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 40 Şekil 7.19: (7.22) Eşitliklerini gerçekleştiren devre
- 41. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 41 Şekil 7.20: (7.22) EĢitliklerinin çok çıkıĢlı tek devre olarak gerçekleĢtirilmesi
- 42. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 42 f1 =  m(2,3,5,7,8,9,10,11,13,15) f2 =  m(2,3,5,6,7,10,11,14,15) f3 =  m(6,7,8,9,13,14,15) (7.23) ÖRNEK 2: Diğer bir dört giriĢli-üç çıkıĢlı devre tasarımı (7.23) eĢikliklerinin minimum ifadelerini bulmak için ġekil 7.21 deki Karnaugh haritaları kullanlmıĢtır.
- 43. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 43 f1=bd + b’c + ab’ f2=c + a’bd f3= bc + ab’c’ + abd ac’d veya (7.23.a) Önce ġekil (7.21) de verilen Karnaugh haritasından fonksiyonların aĢağıda verilen minimum ifadeleri bulunur. Bu fonksiyonlar 10 kapı ve 25 kapı giriĢi ile gerçekleĢtirilebilir.
- 44. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 44 ġekil 7.21
- 45. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 45 Karnaugh haritalarından a' bd ( f2 den), abd ( f3 den), ve ab' c’ ( f3 den) terimlerinin f1’ in içinde kullanılabileceği kolayca görülmekedir. Eğer bd terimi yerine a' bd + abd kullanılırsa bd terimini gerçekleĢtirecek olan kapı elimine edilir. f1 ‘ in içindeki m10 ve m11 terimleri b'e, ve ab' c' ( f3 teki ) terimlerinin içinde zaten bulunmaktadır ve bunlar aynı zamanda m8 ve m9; terimlerinide kapsamada kullanılabilir ve ab‘ terimini gerçekleştirecek olan kapı elimine edilebilir. Bu durumda en uygun çözüm aşağıdaki eşitliklrden elde edilir: f1=a’bd + abd + ab’c’ + b’c f2=c + a’bd f3=bc + ab’c’ + abd (7.23.b)
- 46. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 46 (7.23.b) eĢitlikleri 8 kapı ve 22 kapı giriĢi gerektirir ve 2 kapı 3 kapı giriĢi tasarruf ediĢlmiĢ olur. Çok çıkıĢlı devre tasarlanırken bazı durumlarda komĢu 1 lerin aynı guruba alıması daha az devre elemanı kullanma yerine daha fazla devre elemanı kullanmayı gerektireceğinden uygun değildir. Veya baĢka bi değiĢle en çok sayıda ortak terim kullanmak her zaman en iyi çözüm olmayabilir. Bunun örneği ileride ġekil 7.23 de gösterilecektir. (Ġki fonksiyon arasında ortak kullanılan terimlerin altları çizilmiĢtir.)
- 47. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 47 Çok ÇıkıĢlı devre tasarımı için Karnaugh haritalarından gerekli temel (prime) gurupların (implicant’ ların belirlenmesi Ġki-Basamaklı çok çıkıĢlı devre tasarımında ilk adım gerekli temel (prime) gurupların (implikants) bulunmasıdır. Bunu yaparken çok dikkatli olmamız gereken bir özelliği gözden kaçırmamak lazım. Buda birtek fonksiyon için gerekli temel gurup (essential prime implicant) olan bir gurup çok çıkışlı devre tasarımı için gerekli temel gurup (essential prime implicant) olamayabilir. Örneğin Şekil 7.21 de, bd terimi f1 fonksiyonu için gerekli temel gurup (essential prime implicant) (m5 ‘i içeren tek temel gurup) olmasına karĢın, çok çıkıĢlı devre tasarımı için gerekli temel guruplardan biri değildir.
- 48. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 48 Bunun nedeni (bd nin temel guruplardan birisi olmaması) m5 aynı zamanda f2 ‘nin haritasında da gözükmesi, bu nedenle de f1 ve f2 fonksiyonlarının ortak bir terimi tarafından kapsama alınabileceğidir. f1 = a’c’d+abd+ab’c’d f2 = bc’d’+abcd+bcd’ Bu iki fonksiyonu Karnaugh haritalarına taĢıyıp en iyi çözümü veren gerekli temel gurupları (essential prime implicans) bulalım. Sonuç bir sonraki slaytta (ġekil 7.22) gösterilmiĢtir. Örnek 1: Aşağdaki iki fonksiyonu göz önüne alalım;
- 49. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 49 (a) En iyi çözüm (b) Bu çözüm bir fazla kapı gerektiriyor Şekil 7.22
- 50. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 50 f1=a’b’d’+a’bc’d+a’bd’+abcd’ f2=a’b’c’+a’bd’+abc’d’+bcd’ Örnek 2: Aşağdaki iki fonksiyonu göz önüne alalım: Bu iki fonksiyonu Karnaugh haritalarına taĢıyıp en iyi çözümü veren gerekli temel gurupları (essential prime implicans) bulalım. Sonuç bir sonraki slaytta (ġekil 7.23) gösterilmiĢtir.
- 51. Ġki basamaklı (Düzeyli) Çok ÇıkıĢlı Devre Tasarımı KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 51 (a) En çok ortak terimle elde edilen çözüm: 8 kapı, 22 kapı giriĢi gerekli (b) En iyi çözüm: 7 kapı, 18 kapı giriĢi gerekli ve ortak terim yok. ġekil 7.23
- 52. Çok çıkıĢlı NOR ve NAND kapısı devreleri KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 52 F1 = [(a + b’ )c + d](e’ + f ) F2 = [(a + b’ )c + g’ ](e’ + f )h ÖRNEK 1: AĢağıda verilen iki fonksiyonu çok çıkıĢlı NOR devresi olarak geçekleĢtirelim. Ġstenen NOR devresi olduğundan önce OR-AND devresini kurmamız doğru yaklaĢımdır bu devre ġekil 7.24.a da verilmiĢ ve NOR devresine dönüĢümü ġekil 7.24.b de verilmiĢtir.
- 53. Çok çıkıĢlı NOR ve NAND kapısı devreleri KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 53 1. Basamak2. Basamak3. Basamak4. Basamak (a) AND ve OR devresi (b) Eşdeğer NOR devresi Şekil 7.24 Çok basamaklı NOR devresi dönüşümü
- 54. Çok çıkıĢlı NOR ve NAND kapısı devreleri KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 54 ÖRNEK 2: AĢağıda verilen iki fonksiyonu çok çıkıĢlı NAND devresi olarak gerçekleĢtirelim. f1=(ab+c’d+n)h+(a+e’)g+k f2=(c’d+eh+g)k+(a+e’)g+b Ġstenen NAND devresi olduğundan önce AND-OR devresini kurmamız doğru yaklaĢımdır. Bu devre ġekil 7.25.a da verilmiĢ ve NAND devresine dönüĢümü ġekil 7.25.b de verilmiĢtir.
- 55. Çok çıkıĢlı NOR ve NAND kapısı devreleri KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 55 Şekil 7.25.a Çok basamaklı AND-OR devresi
- 56. Çok çıkıĢlı NOR ve NAND kapısı devreleri KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 56 Şekil 7.25.b. Çok basamaklı NAND devresi dönüşümü
- 57. Kaynakça • 1.Hüseyin EKİZ, Mantık Devreleri, Değişim Yayınları, 4. Baskı, 2005 • 2.Thomas L. Floyd, Digital Fundamentals, Prentice-Hall Inc. New Jersey, 2006 • 3.M. Morris Mano, Michael D. Ciletti, Digital Design, Prentice-Hall, Inc.,New Jersey, 1997 • 4.Hüseyin Demirel, Dijital Elektronik, Birsen Yayınevi, İstanbul, 2012 KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 57
- 58. Teşekkür Ederim Sağlıklı ve mutlu bir hafta geçirmeniz temennisiyle, iyi çalışmalar dilerim… KBUZEM Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 58


![ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK
DEVRELERĠ, NAND VE NOR KAPILARI
KBUZEM
Karabük Üniversitesi
Uzaktan Eğitim Uygulama ve Araştırma Merkezi
4
Z’ nin ifadesini baĢka türlü yazarak üç basamaklı
devre elde edebiliriz. Bu kısmi çarpma ile
gerçekleĢtirilebilir.
Z= (AB + C)[(D + E) + FG ] + H
= AB(D + E) + C(D + E) + ABFG + CFG + H](https://image.slidesharecdn.com/h7blm2211-171015093707/85/H7-blm221-1-4-320.jpg)






![KBUZEM
Karabük Üniversitesi
Uzaktan Eğitim Uygulama ve Araştırma Merkezi
12
ÇOK DÜZEYLĠ (BASAMAKLI) MANTIK
DEVRELERĠ, NAND VE NOR KAPILARI
Üç basamaklı AND çıkıĢlı devre elde edebilmek için (7.4)
denklemine önce (X+Y)(X+Z)=X+YZ teoremi
uygulayalım:
f = [c + d(a’ + b )][c’ + d’ (a+b)] (7.5)
elde edilir. (7.5) eĢitliği dört basamaklı devre gerektirir.
KöĢeli parantez içindeki ifadeleri çarpıp açarsak :
f = (c + a’ d + bd )(c’ + ad’ +bd’ ) (7.6)
elde edilir. (7.6) eĢitliği üç basamaklı AND-OR-AND
devresi olarak ġekil 7.7 verildiği gibi gerçekleĢtirilir:](https://image.slidesharecdn.com/h7blm2211-171015093707/85/H7-blm221-1-12-320.jpg)











![KBUZEM
Karabük Üniversitesi
Uzaktan Eğitim Uygulama ve Araştırma Merkezi
24
ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE
NOR KAPISI DEVRELERĠNĠN TASARIMI
(7.13), (7.14), (7.15) ve (7.16) eĢitlikleri ġekil 7.11 de
gösterildiği gibi, sıra ile AND-OR, NAND-NAND, OR-
NAND, NOR-OR devrelerine karĢılık gelmektedirler.
(7.16) eĢitliğini yeniden aĢağıdaki gibi yazalım:
F = {[A + (B' + C)' + (B + C' + D')' ]'}'
F = A + BC' + B‘ C D = [(A +B C‘ + B’ CD)’ ]'
= [A' • (BC‘ )' • (B‘ CD)‘ ] '
= [A' • (B' + C) • (B + C' + D‘ ) ]'
= A + (B' + C)' + (B + C' + D‘ )'
(7.17)
(7.13)
(7.11) den (7.14)
(7.12) den (7.15)
(7.12) den (7.16)](https://image.slidesharecdn.com/h7blm2211-171015093707/85/H7-blm221-1-24-320.jpg)
![KBUZEM
Karabük Üniversitesi
Uzaktan Eğitim Uygulama ve Araştırma Merkezi
25
ĠKĠ VE ÜÇ BASAMAKLI (DÜZEYLĠ) NAND VE
NOR KAPISI DEVRELERĠNĠN TASARIMI
(7.17) eĢitliği üç bamaklı NOR-NOR-INVERT devresi
verir. Fakat iki basamaklı NOR devresi elde etmek
istiyorsak, minimum SOP yerine minimum POS
(product-of-sums) formu ile baĢlamamız gerekir.
Karnaugh haritasından minimum POS ifadesi
bulunduktan sonra fonksiyon aĢağıdaki gibi iki
basamaklı devre veren formda yazılır:
F=(A+B+C)(A+B’+C’)(A+C’+D)
= {[(A+B+C)(A+B’+C’)(A+C’+D)]’}’
= [(A+B+C)’+(A+B’+C’)’+(A+C’+D)’]’
= (A’B’C’+A’BC+A’CD’)’
= (A’B’C’)’.(A’BC)’.(A’CD’)’
(7.18)
(7.19)
(7.20)
(7.21)](https://image.slidesharecdn.com/h7blm2211-171015093707/85/H7-blm221-1-25-320.jpg)






![KBUZEM
Karabük Üniversitesi
Uzaktan Eğitim Uygulama ve Araştırma Merkezi
32
Çok basamaklı (düzeyli) NAND ve
NOR Kapıları Devreleri
Örnek: AĢağıdaki fonksiyonu NAND devresi ile
geçekleĢtiriniz.
F1=a’ [b’ + c(d + e’ ) + f’ g’ ] + hi’ j + k
ġekil 7.13 görüldüğü gibi devrenin Ģması önce AND-OR
devresi olarak çizilmiĢ ve daha sonra yukarıda anlatıldığı
gibi NAND devresine dönüĢtürülmüĢtür.](https://image.slidesharecdn.com/h7blm2211-171015093707/85/H7-blm221-1-32-320.jpg)




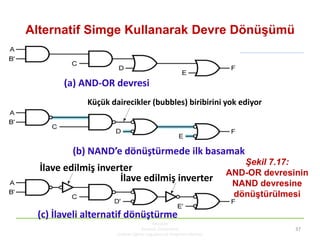















F2 = [(a + b’ )c + g’ ](e’ + f )h
ÖRNEK 1: AĢağıda verilen iki fonksiyonu çok çıkıĢlı
NOR devresi olarak geçekleĢtirelim.
Ġstenen NOR devresi olduğundan önce OR-AND
devresini kurmamız doğru yaklaĢımdır bu devre
ġekil 7.24.a da verilmiĢ ve NOR devresine
dönüĢümü ġekil 7.24.b de verilmiĢtir.](https://image.slidesharecdn.com/h7blm2211-171015093707/85/H7-blm221-1-52-320.jpg)