Himpunan kelas 7
- 1. Pengertian Himpunan Himpunan adalah Kumpulan benda atau objek yang didefinisikan (diterangkan) dengan jelas Himpunan dilambangkan dengan huruf kapital misalnya A, B, C, D, …,Z dan objek-objek dari himpunan itu ditulis diantara dua kurung kurawal dan dipisahkan dengan tanda koma Yang dimaksud diterangkan dengan jelas adalah benda atau objeknya jelas mana yang merupakan anggota dan mana yang bukan anggota dari himpunan itu Contoh: A adalah himpunan bilangan asli kurang dari 10 A = { 1,2,3,4,5,6,7,8,9 }
- 2. Soal : Nyatakan himpunan berikut dalam bentuk notasi pembentuk himpunan 1. B adalah bilangan Asli yang lebih dari 3 dan kurang atau sama dengan 15 2. C adalah bilangan bulat lebih dari atau sama dengan -5 tetapi kurang dari 10 3. D adalah bilangan ganjil kurang dari 20 Jawaban : 1. B = { x | 3 < x ≤ 15 , x A} 2. C = { x | -5 ≤ x < 10 , x B} 3. D = { x | x < 20 , x L }
- 3. Contoh soal : Nyatakan soal di atas dengan cara mendaftar anggotanya Jawaban: 1. B = { x | 3 < x ≤ 15 , x A} = { 4,5,6,7,8,9,10,11,12,13,14,15 } 2. C = { x | -5 ≤ x < 10 , x B } = { -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } 3. D = { x | x < 20 , x L} = { 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 }
- 4. Keanggotaan Suatu Himpunan Contoh: A = { 1, 3, 5, 7, 9 } B = { 2, 4, 6, 8, 10, 12 } 1 A 1 B 2 B 2 A 3 A 3 B 4 B 4 A 5 A 5 B 6 B 6 A 7 A 7 B 8 B 8 A 9 A 9 B 10 B 10 A 12 B 12 A Banyaknya anggota himpunan A dilambangkan dengan n(A) = 5 Banyaknya anggota himpunan B dilambangkan dengan n(B) = 6 Catatan: Lambang dibaca “elemen” atau anggota Lambang dibaca “bukan elemen” atau bukan anggota Lambang n(A), n(B) disebut bilangan kardinal
- 5. HIMPUNAN KOSONG DEFINISI: Himpunan Kosong adalah himpunan yang tidak memiliki anggota dan dilambangkan dengan { } atau Contoh : F = { x | x bilangan prima antara 7 dan 11 } Pada contoh di atas adakah saat ini orang yang tingginya lebih dari 5 meter dan adakah bilangan prima diantara 7 dan 11 ? (coba pikir) Sekarang cobalah kalian membuat notasi himpunan yang mendefinisikan himpunan kosong (waktumu 5 menit) Selanjutnya kerjakan latihan 4 buku paket hal 5
- 6. Himpunan Lepas Definisi: Dua himpunan yang tidak kosong dikatakan saling lepas jika kedua himpunan itu tidak mempunyai satupun anggota yang sama Contoh : L = { 1, 3, 5, 7, 9, 11, 13, 15 } G = { 2, 4, 6, 8, 10, 12, 14, 16 } Coba kalian perhatikan, adakah anggota himpunan L dan G yang sama ? Karena tidak ada anggota himpunan L dan G yang sama maka himpunan L dan G adalah dua himpunan yang saling lepas, jadi L // G Himpunan Tidak Saling Lepas Definisi: Dua himpunan yang tidak kosong dikatakan tidak saling lepas (berpotongan) jika kedua himpunan itu mempunyai anggota yang sama Contoh : P = { 1, 2, 3, 4, 5, 6, 7, 8 } Q = { 2, 4, 6, 8, 10, 12, 14, 16 } Himpunan P dan himpunan Q tidak saling lepas karena mempunyai anggota yang sama (persekutuan) yaitu 2, 4, 6, dan 8, jadi P Q Sekarang kerjakan latihan 9 buku paket halaman 11
- 7. Himpunan Semesta Definisi : Himpunan Semesta adalah himpunan yang memuat semua objek yang dibicarakan Contoh : A = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15} D = { 2,3,5,7,11 } B = { -3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,11 } E = { 0, 2, 4, 6 } C = { 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14 } Perhatikan setiap anggota himpunan A, B, C, D, dan E 1. Apakah setiap anggota himpunan D ada di dalam himpunan A, B, dan C ? 2. Apakah setiap anggota himpunan E ada di dalam himpunan A, B, dan C ? Setiap anggota himpunan D yaitu 2,3,5,7,11 ada di dalam Himpunan A, B, C. Oleh karena itu Himpunan A,B,C adalah Himpunan Semesta dari Himpunan D Setiap anggota Himpunan E yaitu 0,2,4,6 ada di dalam himpunan B dan C, tetapi angka 0 tidak ada di dalam himpunan A. Oleh karena itu Himpunan B dan C merupakan Himpunan semesta dari himpunan E, dan Himpunan A bukan himpunan semesta dari himpunan E Sekarang kerjakan latihan 5 buku paket halaman 6 (waktumu 30 menit)
- 8. HIMPUNAN BAGIAN Definisi: A adalah himpunan bagian dari himpunan B apabila setiap anggota himpunan A juga menjadi anggota himpunan B dilambangkan dengan A B Contoh: S = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 } A = { 0, 1, 2, 3, 4, 5, 6, 7 } ; B = { 1, 2, 3, 4 } ; C = { 6, 7, 8, 9 } a. Apakah himpunan B merupakan himpunan bagian dari himpunan A ? b. Apakah himpunan C merupakan himpunan bagian dari himpunan A ? Perhatikan setiap anggota himpunan A, B, C a. Karena setiap anggota himpunan B juga merupakan anggota himpunan A maka himpunan B merupakan himpunan bagian dari himpunan A, jadi B A b. Karena ada anggota himpunan C yaitu 8 dan 9 tidak terdapat di dalam himpunan A maka himpunan C bukan himpunan bagian dari himpunan A, jadi C A
- 9. Rumus Banyaknya Himpunan Bagian Jika suatu himpunan mempunyai anggota sebanyak n(A) maka banyaknya himpunan bagian dari A adalah sebanyak 2n(A) Contoh: Tentukan banyaknya himpunan bagian yang mungkin dari himpunan berikut 1. A = { a, b, c } 2. B = { 1, 2, 3, 4, 5 } 3. C = { 2, 3, 4, 5, 6, 7, 8 } Jawab: 1. n(A) = 3 maka banyaknya himpunan bagian yang mungkin dari A adalah 23 = 2 x 2 x 2 = 8 2. n(B) = 5 maka banyaknya himpunan bagian yang mungkin dari B adalah 25 = 2 x 2 x 2 x 2 x 2 = 32 3. n(C) = 7 maka banyaknya himpunan bagian yang mungkin dari C adalah 27 = 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128
- 10. Himpunan Sama Definisi: Dua himpunan dikatakan sama apabila setiap anggota kedua himpunan itu sama bentuk dan jumlahnya Contoh : A = { a, I, u, e, o } ; B = { u, a, I, o, e } Kedua himpunan A dan B anggota-anggotanya sama yaitu a,I,u,e, dan o maka himpunan A = B Himpunan Ekuivalen Definisi: Dua himpunan dikatakan Ekuivalen apabila jumlah anggota kedua himpunan itu sama tetapi bendanya ada yang tidak sama Contoh : P = { a, I, u, e, o } ; Q = { 1, 2, 3, 4, 5 } Kedua himpunan P dan Q anggota-anggotanya tidak sama tetapi jumlah anggotanya sama maka himpunan P Ekuivalen dengan Q, jadi ( P ~ Q )
- 11. Irisan Dua Himpunan (Interseksi) Definisi: Irisan himpunan A dan B ditulis A B adalah himpunan semua objek yang menjadi anggota himpunan A sekaligus menjadi anggota himpunan B Contoh: Bila P = {a, b, c, d, e } dan Q = {d, e, f, g, h }. Tentukan P Q Jawab : P Q = { d, e } Gabungan Dua Himpunan ( Union) Definisi: Gabungan himpunan A dan B ditulis A B adalah himpunan semua objek yang menjadi anggota himpunan A atau menjadi anggota himpunan B Contoh: Bila P = {a, b, c, d, e } dan Q = {d, e, f, g, h }. Tentukan P Q Jawab : P Q = { a, b, c, d, e, f, g, h }
- 12. Diagram Venn Langkah-langkah menggambar diagram venn 1. Daftarlah setiap anggota dari masing-masing himpunan 2. Tentukan mana anggota himpunan yang dimiliki secara bersama-sama 3. Letakkan anggota himpunan yang dimiliki bersama ditengah-tengah 4. Buatlah lingkaran sebanyak himpunan yang ada yang melingkupi anggota bersama tadi 5. Lingkaran yang dibuat tadi ditandai dengan nama-nama himpunan 6. Selanjutnya lengkapilah anggota himpunan yang tertulis didalam lingkaran sesuai dengan daftar anggota himpunan itu 7. Buatlah segiempat yang memuat lingkaran-lingkaran itu, dimana segiempat ini menyatakan himpunan semestanya dan lengkapilah anggotanya apabila belum lengkap
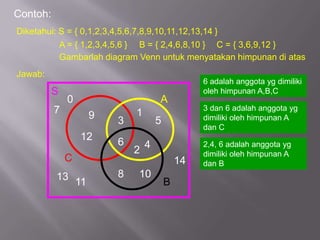
- 13. Contoh: Diketahui: S = { 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14 } A = { 1,2,3,4,5,6 } B = { 2,4,6,8,10 } C = { 3,6,9,12 } Gambarlah diagram Venn untuk menyatakan himpunan di atas Jawab: 6 adalah anggota yg dimiliki S oleh himpunan A,B,C 0 A 7 3 dan 6 adalah anggota yg 9 1 dimiliki oleh himpunan A 3 5 dan C 12 6 2 4 2,4, 6 adalah anggota yg dimiliki oleh himpunan A C 14 dan B 13 11 8 10 B
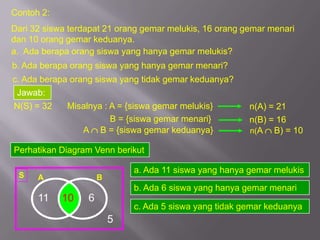
- 14. Contoh 2: Dari 32 siswa terdapat 21 orang gemar melukis, 16 orang gemar menari dan 10 orang gemar keduanya. a. Ada berapa orang siswa yang hanya gemar melukis? b. Ada berapa orang siswa yang hanya gemar menari? c. Ada berapa orang siswa yang tidak gemar keduanya? Jawab: N(S) = 32 Misalnya : A = {siswa gemar melukis} n(A) = 21 B = {siswa gemar menari} n(B) = 16 A B = {siswa gemar keduanya} n(A B) = 10 Perhatikan Diagram Venn berikut a. Ada 11 siswa yang hanya gemar melukis S A B b. Ada 6 siswa yang hanya gemar menari 11 10 6 c. Ada 5 siswa yang tidak gemar keduanya 5
- 15. Contoh 3: Diketahui : S = { x | 10 < x ≤ 20, x B} M = { x | x > 15, x S} N = { x | x > 12, x S} Gambarlah diagram vennya Jawab : S = { x | 10 < x ≤ 20, x B } = { 11,12,13,14,15,16,17,18,19,20 } M = { x | x > 15, x S } = { 16,17,18,19,20} N = { x | x > 12, x S } = { 13,14,15,16,17,18,19,20} M N = { 16,17,18,19,20 } Diagram Vennya adalah sbb: S N 16 18 M 20 11 17 19 13 12 14 15
- 16. Contoh 4: Dari 60 siswa terdapat 20 orang suka bakso, 46 orang suka siomay dan 5 orang tidak suka keduanya. a. Ada berapa orang siswa yang suka bakso dan siomay? b. Ada berapa orang siswa yang hanya suka bakso? c. Ada berapa orang siswa yang hanya suka siomay? Jawab: N(S) = 60 Misalnya : A = {siswa suka bakso} n(A) = 20 B = {siswa suka siomay} n(B) = 46 (A B)c = {tidak suka keduanya} n((A B)c) = 5 Maka A B = {suka keduanya} n(A B) = x {siswa suka bakso saja} = 20 - x n(S) = (20 – x)+x+(46-x)+5 60 = 71 - x {siswa suka siomay saja} = 46 - x X = 71 – 60 = 11 Perhatikan Diagram Venn berikut a. Yang suka keduanya adalah x = 11 orang S b. Yang suka bakso saja adalah A 20-x = 20-11= 9 orang 20 - x x 46 - x B c. Yang suka siomay saja adalah 5 46-x = 46-11= 35 orang