lec33.ppt
Download as PPT, PDF0 likes39 views
The Cauchy Riemann (CR) conditions provide a necessary and sufficient condition for a function f(z) = u(x, y) + iv(x, y) to be analytic in a region. The CR conditions require that the partial derivatives of u and v satisfy ∂u/∂x = ∂v/∂y and ∂u/∂y = -∂v/∂x. If a function satisfies these conditions at all points in a region, then it is analytic in that region. The document proves this using cases where ∆y = 0 and ∆x = 0, showing the derivatives must be equal. Examples are provided to demonstrate checking functions for analytic
1 of 4
Download to read offline
![NPTEL – Physics – Mathematical Physics - 1
Lecture 33
Cauchy Riemann (CR) conditions
CR conditions state that a necessary and a sufficient condition that a
function,
ùëì(ùëß) defined as,
ùëì(ùëß) = ùë¢(ùë•, ùë¶) + ùëñùë£(ùë•, ùë¶)
be analytic in a region ÔÉÇ provides the following conditions (called CR conditions) on the
partial derivatives of ùë¢ ùëéùëõùëë ùë£ are met,
ùúïùë¢
= ùúïùë£
and ùúïùë¢
= ‚àí ùúïùë£
ùúïùë• ùúïùë¶ ùúïùë¶ ùúïùë•
in ÔÉÇ. Additionally it is assumed that the partial derivatives are continuous in ÔÉÇ.
To arrive at the proof of the above equations, let us look at the necessary conditions. For
a function ùëì(ùëß) to be analytic, it should be differentiable in a region ÔÉÇ, that is
ùêøùëñùëö
‚àÜùëß ‚Üí 0
ùëì(ùëß+‚àÜ(ùëß)‚àíùëì(ùëß)
‚àÜùëß
= ùëì‚Ä≤ (ùëß)
ùë¢(ùë• + ‚àÜùë•, ùë¶ + ‚àÜùë¶) + ùëñùë£ (ùë• + ‚àÜùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶) + ùëñùë£(ùë•, ùë¶)
‚àÜùë• + ùëñ‚àÜùë¶
‚àÜùë•‚Üí0
ùêøùëñùëö
‚àÜù붂Üí0
ùêøùëñùëö
must exist and should be independent of the manner in ‚àÜùëß approaches zero. Two
possibilities are apparent for that to happen.
Case A
‚àÜùë¶ = 0, ‚àÜùë• ‚Üí 0
For which ùëì‚Ä≤(ùëß) is defined as,
ùëì‚Ä≤(ùëß) = ‚àÜùë•‚Üí0
ùêøùë° ùë¢(ùë• + ‚àÜùë•, ùë¶) ‚àí ùë¢(ùë•, ùë¶)
‚àÜùë•
+ ùëñ [
ùë£(ùë• + ‚àÜùë•, ùë¶)ùë£(ùë•, ùë¶)
‚àÜùë•
]
= + ùëñ
ùúïùë¢ ùúïùë£
ùúïùë• ùúïùë•
Assuming that the partial derivatives exist.
Joint initiative of IITs and IISc – Funded by MHRD Page 12 of 66](https://image.slidesharecdn.com/lec33-231023101222-f1d15af4/85/lec33-ppt-1-320.jpg)
![NPTEL – Physics – Mathematical Physics - 1
Case B
‚àÜùë¶ ‚Üí 0, ‚àÜùë• = 0
In this case,
ùëì‚Ä≤(ùëß) = ‚àÜù붂Üí0
ùêøùëñùëö ùë¢(ùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶)
ùëñ‚àÜùë•
+
ùë£(ùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë£(ùë•, ùë¶)
‚àÜùë¶
= ùúïùë¢
+ ùëñùúïùë£
ùúïùë¶ ùúïùë¶
Of course, these two cases will have to yield identical results. Thus
ùúïùë¢ ùúïùë£
ùúïùë•
+ ùëñ
ùúïùë•
ùúïùë¢ ùúïùë£
= ‚àíùëñ
ùúï
ùë¶
+
ùúïùë¶
Or, =
ùúïùë¢ ùúïùë£
ùúïùë• ùúïùë¶ ùúïùë•
and = ‚àíùëñ
ùúïùë£ ùúïùë¢
ùúïùë¶
Next we look at the sufficiency conditions. Since and
ùúïùë¢
ùúïùë•
ùúïùë¢
ùúïùë¶
are assumed to be
continuous, we have
‚àÜùë¢ = ùë¢(ùë• + ‚àÜùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶)
= [ùë¢(ùë• + ‚àÜùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶ + ‚àÜùë¶)] + [ùë¢(ùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶)]
Where the second and third terms are subtracted and added.
Hence ‚àÜùë¢ =
ùúïùë¢
‚àÜùë• +
ùúïùë¢
‚àÜùë¶
ùúïùë• ùúïùë¶
Similarly ‚àÜùë£ =
ùúïùë£
‚àÜùë• +
ùúïùë£
‚àÜùë¶
ùúïùë• ùúïùë¶
Thus ‚àÜùë§ = ‚àÜùë¢ + ùëñ‚àÜùë£ = ( + ùëñ ) ‚àÜùë• + (
ùúïùë¢
ùúïùë• ùúïùë¶
ùúïùë£ ùúïùë¢
ùúïùë¶
+ ùëñ ) ‚àÜùë¶
ùúïùë£
ùúïùë¶
Changing the second bracket using CR conditions
‚àÜùë§ = ( + ùëñ ) ‚àÜùë• + (‚àí + ùëñ ) ‚àÜùë¶
ùúïùë¢ ùúïùë£
ùúïùë• ùúïùë• ùúïùë• ùúïùë•
ùúïùë£ ùúïùë¢
= ( + ùëñ ) (ùë• + ùëñ‚àÜùë¶)
Joint initiative of IITs and IISc – Funded by MHRD Page 13 of 66
ùúïùë¢ ùúïùë£
ùúïùë• ùúïùë•](https://image.slidesharecdn.com/lec33-231023101222-f1d15af4/85/lec33-ppt-2-320.jpg)


Recommended
lec38.ppt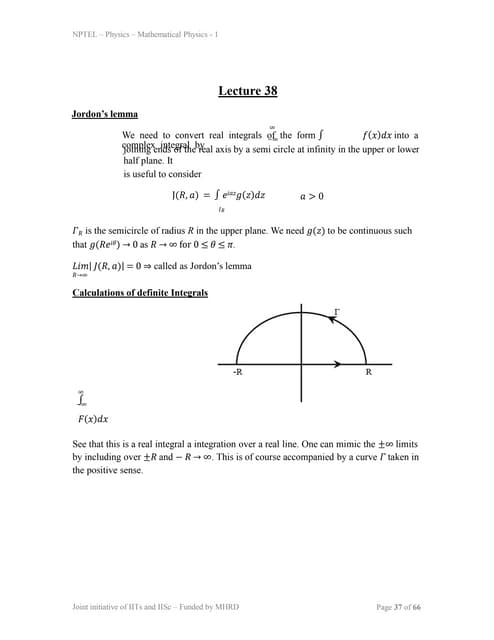



lec38.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) Jordan's lemma is used to convert real integrals over the infinite real axis into complex integrals over a contour enclosing the real axis in the complex plane.
2) Several examples are provided of using residues and Jordan's lemma to evaluate definite integrals over the real line or infinite intervals that involve functions with poles, including integrals of x^2, sin(x)/x, 1/(x^2+a^2)^2, and sin(x)/(x(x^2+a^2)).
3) The technique involves closing the contour with a semicircle at infinity where the integral over the semicircle goes to zero by Jordan's lemma, leaving the original integral equal to the residue theorem applied to theDual Spaces of Generalized Cesaro Sequence Space and Related Matrix Mapping



Dual Spaces of Generalized Cesaro Sequence Space and Related Matrix Mappinginventionjournals
Ã˝
In this paper we define the generalized Cesaro sequence spaces 푐푒푠(푝, 푞, 푠). We prove the space 푐푒푠(푝, 푞, 푠) is a complete paranorm space. In section-2 we determine its Kothe-Toeplitz dual. In section-3 we establish necessary and sufficient conditions for a matrix A to map 푐푒푠 푝, 푞, 푠 to 푙∞ and 푐푒푠(푝, 푞, 푠) to c, where 푙∞ is the space of all bounded sequences and c is the space of all convergent sequences. We also get some known and unknown results as remarks.lec40.ppt



lec40.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
Complex analysis deals with complex-valued functions of complex variables. Some key concepts covered in the document include:
- Complex functions can be expressed in either Cartesian (z = x + iy) or polar (z = reiθ) form.
- For a complex function f(z) to be differentiable, it must satisfy the Cauchy-Riemann conditions.
- Analytic functions are differentiable at every point in their domain. For example, ez is analytic everywhere while zÃÖ is analytic nowhere.
- Branch cuts arise for multi-valued functions like √z, with the line between θ = 2π and θ = 4π representing one branch cut.Complex differentiation contains analytic function.pptx



Complex differentiation contains analytic function.pptxjyotidighole2
Ã˝
This document provides an overview of analytic functions in engineering mathematics. It defines analytic functions as functions whose derivatives exist in some neighborhood of a point, making them continuously differentiable. The Cauchy-Riemann equations are derived as necessary conditions for a function to be analytic. It also defines entire functions as analytic functions over the entire finite plane. Examples of entire functions include exponential, sine, cosine, and hyperbolic functions. The document discusses analyticity in both Cartesian and polar coordinates.lec23.ppt



lec23.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) The document discusses representation of the Dirac delta function in cylindrical and spherical coordinate systems. It shows that δ(r - r') = δ(ρ - ρ')δ(φ - φ')δ(z - z')/ρ in cylindrical coordinates and δ(r - r') = δ(r - r')δ(θ - θ')δ(φ - φ')/r^2 in spherical coordinates.
2) It also derives the important relation ∇^2(1/r) = -4πδ(r) and shows its application to the Laplace equation for electrostatic potential.
3) The completeness of eigenfunctions of harmonic oscillators and LegendLeast Square Plane and Leastsquare Quadric Surface Approximation by Using Mod...



Least Square Plane and Leastsquare Quadric Surface Approximation by Using Mod...IOSRJM
Ã˝
Now a days Surface fitting is applied all engineering and medical fields. Kamron Saniee ,2007 find a simple expression for multivariate LaGrange’s Interpolation. We derive a least square plane and least square quadric surface Approximation from a given N+1 tabular points when the function is unique. We used least square method technique. We can apply this method in surface fitting also.One solution for many linear partial differential equations with terms of equ...



One solution for many linear partial differential equations with terms of equ...Lossian Barbosa Bacelar Miranda
Ã˝
We disclose a simple and straightforward method of solving single-order linear partial differential equations. The advantage of the method is that it is applicable to any orders and the big disadvantage is that it is restricted to a single order at a time. As it is very easy compared to classical methods, it has didactic value.A Probabilistic Algorithm for Computation of Polynomial Greatest Common with ...



A Probabilistic Algorithm for Computation of Polynomial Greatest Common with ...mathsjournal
Ã˝
- The document presents a probabilistic algorithm for computing the polynomial greatest common divisor (PGCD) with smaller factors.
- It summarizes previous work on the subresultant algorithm for computing PGCD and discusses its limitations, such as not always correctly determining the variant τ.
- The new algorithm aims to determine τ correctly in most cases when given two polynomials f(x) and g(x). It does so by adding a few steps instead of directly computing the polynomial t(x) in the relation s(x)f(x) + t(x)g(x) = r(x).A PROBABILISTIC ALGORITHM FOR COMPUTATION OF POLYNOMIAL GREATEST COMMON WITH ...



A PROBABILISTIC ALGORITHM FOR COMPUTATION OF POLYNOMIAL GREATEST COMMON WITH ...mathsjournal
Ã˝
In the earlier work, Knuth present an algorithm to decrease the coefficient growth in the Euclidean
algorithm of polynomials called subresultant algorithm. However, the output polynomials may have a
small factor which can be removed. Then later, Brown of Bell Telephone Laboratories showed the
subresultant in another way by adding a variant called ùúè and gave a way to compute the variant.
Nevertheless, the way failed to determine everyùúè correctly.
In this paper, we will give a probabilistic algorithm to determine the variant ùúè correctly in most cases by
adding a few steps instead of computing ùë°(ùë•) when given ùëì(ùë•) andùëî(ùë•) ‚àà ‚Ñ§[ùë•], where ùë°(ùë•) satisfies that
ùë†(ùë•)ùëì(ùë•) + ùë°(ùë•)ùëî(ùë•) = ùëü(ùë•), here ùë°(ùë•), ùë†(ùë•) ‚àà ‚Ñ§[ùë•]
Matrix Transformations on Some Difference Sequence Spaces



Matrix Transformations on Some Difference Sequence SpacesIOSR Journals
Ã˝
The sequence spaces ùëô‚àû(ùë¢,ùë£,Œî), ùëê0(ùë¢,ùë£,Œî) and ùëê(ùë¢,ùë£,Œî) were recently introduced. The matrix classes (ùëê ùë¢,ùë£,Œî :ùëê) and (ùëê ùë¢,ùë£,Œî :ùëô‚àû) were characterized. The object of this paper is to further determine the necessary and sufficient conditions on an infinite matrix to characterize the matrix classes (ùëê ùë¢,ùë£,Œî ‚à∂ùëèùë†) and (ùëê ùë¢,ùë£,Œî ‚à∂ ùëôùëù). It is observed that the later characterizations are additions to the existing oneslec34.ppt



lec34.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1. The document discusses analytic functions of complex variables through examples. It defines analytic functions as those whose derivatives of all orders exist in the region of analyticity.
2. The Cauchy-Riemann equations are derived and their implications are explored, including that they imply the Laplace equation and orthogonality of level curves.
3. Several examples are worked through to determine if functions are analytic by checking if they satisfy the Cauchy-Riemann equations. The Cauchy-Riemann equations are also derived in polar coordinates.C0560913



C0560913IOSR Journals
Ã˝
IOSR Journal of Mathematics(IOSR-JM) is an open access international journal that provides rapid publication (within a month) of articles in all areas of mathemetics and its applications. The journal welcomes publications of high quality papers on theoretical developments and practical applications in mathematics. Original research papers, state-of-the-art reviews, and high quality technical notes are invited for publications.Study Material Numerical Differentiation and Integration



Study Material Numerical Differentiation and IntegrationMeenakshisundaram N
Ã˝
This document discusses numerical differentiation and integration using Newton's forward and backward difference formulas. It provides examples of using these formulas to calculate derivatives from tables of ordered data pairs. Specifically, it shows how to calculate derivatives at interior points using central difference formulas, and at endpoints using forward or backward formulas depending on if the point is near the start or end of the data range. Formulas are derived for calculating the first and second derivatives, and examples are worked through to find acceleration and rates of cooling from given temperature-time tables.Functions of severable variables



Functions of severable variablesSanthanam Krishnan
Ã˝
Partial differentiation, total differentiation, Jacobian, Taylor's expansion, stationary points,maxima & minima (Extreme values),constraint maxima & minima ( Lagrangian multiplier), differentiation of implicit functions. lec32.ppt



lec32.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
The document discusses properties of complex numbers including:
- Commutativity and associativity of addition and multiplication
- Additive and multiplicative identities and inverses
- Conjugates, modulus, and triangle inequality
- Polar form representation using modulus and argument
- Exponential form for products, quotients, and powers
- Roots of complex numbers and finding nth roots
- Representing functions of a complex variable using modulus and argumentStrong convexity on gradient descent and newton's method



Strong convexity on gradient descent and newton's methodSEMINARGROOT
Ã˝
Gradient descent is an optimization algorithm used to find local minima of differentiable functions. It works by taking steps in the negative direction of the gradient of the function at the current point. Newton's method approximates the function using a second-order Taylor expansion and finds the minimum of the quadratic approximation to determine the next step. The gradient descent step size can be shown to decrease the function value when the function is strongly convex or satisfies the Lipschitz condition.A05330107



A05330107IOSR-JEN
Ã˝
1) The document presents a wavelet collocation method for numerically solving nth order Volterra integro-differential equations. It expands the unknown function as a series of Chebyshev wavelets of the second kind with unknown coefficients.
2) It states and proves a uniform convergence theorem that establishes the convergence of approximating the solution using truncated Chebyshev wavelet series expansions.
3) The paper demonstrates the validity and applicability of the proposed method through some illustrative examples of solving integro-differential equations using the Chebyshev wavelet collocation approach.Schwarzchild solution derivation



Schwarzchild solution derivationHassaan Saleem
Ã˝
A derivation of the Schwarzchild solution is presented with all relevant information. I have used this slides to teach Schwarzchild solution at my youtube channel. Here is the link
https://www.youtube.com/watch?v=ixhgvnGQZHM&t=1635sSome Common Fixed Point Results for Expansive Mappings in a Cone Metric Space



Some Common Fixed Point Results for Expansive Mappings in a Cone Metric SpaceIOSR Journals
Ã˝
The purpose of this work is to extend and generalize some common fixed point theorems for Expansive type mappings in complete cone metric spaces. We are attempting to generalize the several well- known recent results. Mathematical subject classification; 54H25, 47H10lec14.ppt



lec14.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
The document discusses matrix representations of operators and changes of basis in quantum mechanics. Some key points:
- Matrix elements of an operator are computed using a basis of kets. The expectation value of an operator is computed from its matrix elements and the state vectors.
- If two operators commute, they have the same set of eigenkets.
- A change of basis is a unitary transformation that relates two different sets of basis kets that span the same space. It establishes a link between the two basis representations.
- Linear algebra concepts like linear independence of eigenvectors and Hermitian operators having real eigenvalues are important in quantum mechanics.PRODUCT RULES



PRODUCT RULESNumanUsama
Ã˝
This document discusses vector calculus concepts and operations involving the del operator (‚àá). It provides proofs and examples of:
1. Curl of the gradient of a scalar field is equal to zero.
2. The curl of the curl of a vector field is equal to the gradient of the divergence minus the Laplace operator.
3. The curl of the product of a scalar field and a vector field is equal to the scalar field times the curl of the vector field plus the cross product of the gradient of the scalar field and the vector field.
It also defines the Laplace operator and discusses its representation in spherical coordinates.BSC_COMPUTER _SCIENCE_UNIT-2_DISCRETE MATHEMATICS



BSC_COMPUTER _SCIENCE_UNIT-2_DISCRETE MATHEMATICSRai University
Ã˝
This document provides an introduction to definite integration and its applications. It defines indefinite integration as finding the integral or primitive function F(x) of a function f(x). Definite integration involves finding the area under a curve defined by a function f(x) over a specified interval. Standard formulae for integrating common functions like polynomials, trigonometric functions, and exponentials are provided. Methods for integrating functions using substitution and integration by parts are described. Examples of applying these techniques to evaluate definite integrals are also given.Some properties of two-fuzzy Nor med spaces



Some properties of two-fuzzy Nor med spacesIOSR Journals
Ã˝
The study sheds light on the two-fuzzy normed space concentrating on some of their properties like convergence, continuity and the in order to study the relationship between these spacesHERMITE SERIES



HERMITE SERIESMANISH KUMAR
Ã˝
This document discusses Hermite polynomials and their properties. It begins by introducing the Hermite equation, which arises from the theory of the linear harmonic oscillator. The Hermite equation is then solved using a series solution approach. Explicit formulas for the Hermite polynomials Hn(x) are derived for n=0,1,2,3,... using properties of the Hermite equation like recursion relations. Key properties of the Hermite polynomials like generating functions, even/odd behavior, Rodrigue's formula, orthogonality, and recurrence relations are also proved.doc



docSiddharth Pujari
Ã˝
This document is an internship project report submitted by Siddharth Pujari to the Indian Institute of Space Science and Technology. The report focuses on advanced control system design for aircraft and simulating aircraft trajectory. It includes modeling an aircraft's state space model in MATLAB to test controllability. The report also covers theoretical aspects of stability of linear systems, linearizing nonlinear models, controllability of linear systems using the Kalman criterion and transition matrix, and applying these concepts to simulate aircraft controllability in MATLAB.Semana 24 funciones iv √°lgebra uni ccesa007



Semana 24 funciones iv √°lgebra uni ccesa007Demetrio Ccesa Rayme
Ã˝
The document discusses algebra topics including the equality of functions, operations between functions, and function composition. It provides definitions and examples of equal functions, adding, subtracting, multiplying, and dividing functions. Examples are given to demonstrate calculating these operations between functions and finding the domain, range, and graph of the resulting functions.Differential Geometry for Machine Learning



Differential Geometry for Machine LearningSEMINARGROOT
Ã˝
References:
Differential Geometry of Curves and Surfaces, Manfredo P. Do Carmo (2016)
Differential Geometry by Claudio Arezzo
Youtube: https://youtu.be/tKnBj7B2PSg
What is a Manifold?
Youtube: https://youtu.be/CEXSSz0gZI4
Shape analysis (MIT spring 2019) by Justin Solomon
Youtube: https://youtu.be/GEljqHZb30c
Tensor Calculus
Youtube: https://youtu.be/kGXr1SF3WmA
Manifolds: A Gentle Introduction,
Hyperbolic Geometry and Poincaré Embeddings by Brian Keng
Link: http://bjlkeng.github.io/posts/manifolds/,
http://bjlkeng.github.io/posts/hyperbolic-geometry-and-poincare-embeddings/
Statistical Learning models for Manifold-Valued measurements with application to computer vision and neuroimaging by Hyunwoo J.Kim
lec19.ppt



lec19.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
This document discusses finding the eigenvalues and eigenfunctions of a spin-1/2 particle pointing along an arbitrary direction. It shows that the eigenvalue equation reduces to a set of two linear, homogeneous equations. The eigenvalues are found to be ±1/2, and the corresponding eigenvectors are written in terms of the direction angles θ and Φ. As an example, it shows that for a spin oriented along the z-axis, the eigenvectors reduce to simple forms as expected for a spin-1/2 particle. It also introduces the Gauss elimination method for numerically solving systems of linear equations that arise in eigenvalue problems.lec31.ppt



lec31.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
Complex numbers allow solutions to equations like x2 + 1 = 0 by extending real numbers to include imaginary numbers. A complex number z is defined as z = x + iy, where x and y are real numbers and i is the imaginary unit equal to ‚àö-1. Complex numbers can be added and multiplied following specific rules, such as z1 + z2 = (x1 + x2) + i(y1 + y2) for addition and z1z2 = (x1x2 - y1y2) + i(y1x2 + x1y2) for multiplication. The inverse of a complex number z is calculated as z-1 = (x/(x2+ylec42.ppt



lec42.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) The document discusses examples of calculating the Jacobian of transformations. It defines the Jacobian as the determinant of the partial derivatives of the transformed coordinates.
2) It then discusses Möbius transformations, which are fractional linear transformations of the form (az+b)/(cz+d). The Jacobian of a Möbius transformation depends only on z.
3) Several examples are given of using Möbius transformations to map one geometric region to another, such as mapping a circle to a line.More Related Content
Similar to lec33.ppt (20)
A PROBABILISTIC ALGORITHM FOR COMPUTATION OF POLYNOMIAL GREATEST COMMON WITH ...



A PROBABILISTIC ALGORITHM FOR COMPUTATION OF POLYNOMIAL GREATEST COMMON WITH ...mathsjournal
Ã˝
In the earlier work, Knuth present an algorithm to decrease the coefficient growth in the Euclidean
algorithm of polynomials called subresultant algorithm. However, the output polynomials may have a
small factor which can be removed. Then later, Brown of Bell Telephone Laboratories showed the
subresultant in another way by adding a variant called ùúè and gave a way to compute the variant.
Nevertheless, the way failed to determine everyùúè correctly.
In this paper, we will give a probabilistic algorithm to determine the variant ùúè correctly in most cases by
adding a few steps instead of computing ùë°(ùë•) when given ùëì(ùë•) andùëî(ùë•) ‚àà ‚Ñ§[ùë•], where ùë°(ùë•) satisfies that
ùë†(ùë•)ùëì(ùë•) + ùë°(ùë•)ùëî(ùë•) = ùëü(ùë•), here ùë°(ùë•), ùë†(ùë•) ‚àà ‚Ñ§[ùë•]
Matrix Transformations on Some Difference Sequence Spaces



Matrix Transformations on Some Difference Sequence SpacesIOSR Journals
Ã˝
The sequence spaces ùëô‚àû(ùë¢,ùë£,Œî), ùëê0(ùë¢,ùë£,Œî) and ùëê(ùë¢,ùë£,Œî) were recently introduced. The matrix classes (ùëê ùë¢,ùë£,Œî :ùëê) and (ùëê ùë¢,ùë£,Œî :ùëô‚àû) were characterized. The object of this paper is to further determine the necessary and sufficient conditions on an infinite matrix to characterize the matrix classes (ùëê ùë¢,ùë£,Œî ‚à∂ùëèùë†) and (ùëê ùë¢,ùë£,Œî ‚à∂ ùëôùëù). It is observed that the later characterizations are additions to the existing oneslec34.ppt



lec34.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1. The document discusses analytic functions of complex variables through examples. It defines analytic functions as those whose derivatives of all orders exist in the region of analyticity.
2. The Cauchy-Riemann equations are derived and their implications are explored, including that they imply the Laplace equation and orthogonality of level curves.
3. Several examples are worked through to determine if functions are analytic by checking if they satisfy the Cauchy-Riemann equations. The Cauchy-Riemann equations are also derived in polar coordinates.C0560913



C0560913IOSR Journals
Ã˝
IOSR Journal of Mathematics(IOSR-JM) is an open access international journal that provides rapid publication (within a month) of articles in all areas of mathemetics and its applications. The journal welcomes publications of high quality papers on theoretical developments and practical applications in mathematics. Original research papers, state-of-the-art reviews, and high quality technical notes are invited for publications.Study Material Numerical Differentiation and Integration



Study Material Numerical Differentiation and IntegrationMeenakshisundaram N
Ã˝
This document discusses numerical differentiation and integration using Newton's forward and backward difference formulas. It provides examples of using these formulas to calculate derivatives from tables of ordered data pairs. Specifically, it shows how to calculate derivatives at interior points using central difference formulas, and at endpoints using forward or backward formulas depending on if the point is near the start or end of the data range. Formulas are derived for calculating the first and second derivatives, and examples are worked through to find acceleration and rates of cooling from given temperature-time tables.Functions of severable variables



Functions of severable variablesSanthanam Krishnan
Ã˝
Partial differentiation, total differentiation, Jacobian, Taylor's expansion, stationary points,maxima & minima (Extreme values),constraint maxima & minima ( Lagrangian multiplier), differentiation of implicit functions. lec32.ppt



lec32.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
The document discusses properties of complex numbers including:
- Commutativity and associativity of addition and multiplication
- Additive and multiplicative identities and inverses
- Conjugates, modulus, and triangle inequality
- Polar form representation using modulus and argument
- Exponential form for products, quotients, and powers
- Roots of complex numbers and finding nth roots
- Representing functions of a complex variable using modulus and argumentStrong convexity on gradient descent and newton's method



Strong convexity on gradient descent and newton's methodSEMINARGROOT
Ã˝
Gradient descent is an optimization algorithm used to find local minima of differentiable functions. It works by taking steps in the negative direction of the gradient of the function at the current point. Newton's method approximates the function using a second-order Taylor expansion and finds the minimum of the quadratic approximation to determine the next step. The gradient descent step size can be shown to decrease the function value when the function is strongly convex or satisfies the Lipschitz condition.A05330107



A05330107IOSR-JEN
Ã˝
1) The document presents a wavelet collocation method for numerically solving nth order Volterra integro-differential equations. It expands the unknown function as a series of Chebyshev wavelets of the second kind with unknown coefficients.
2) It states and proves a uniform convergence theorem that establishes the convergence of approximating the solution using truncated Chebyshev wavelet series expansions.
3) The paper demonstrates the validity and applicability of the proposed method through some illustrative examples of solving integro-differential equations using the Chebyshev wavelet collocation approach.Schwarzchild solution derivation



Schwarzchild solution derivationHassaan Saleem
Ã˝
A derivation of the Schwarzchild solution is presented with all relevant information. I have used this slides to teach Schwarzchild solution at my youtube channel. Here is the link
https://www.youtube.com/watch?v=ixhgvnGQZHM&t=1635sSome Common Fixed Point Results for Expansive Mappings in a Cone Metric Space



Some Common Fixed Point Results for Expansive Mappings in a Cone Metric SpaceIOSR Journals
Ã˝
The purpose of this work is to extend and generalize some common fixed point theorems for Expansive type mappings in complete cone metric spaces. We are attempting to generalize the several well- known recent results. Mathematical subject classification; 54H25, 47H10lec14.ppt



lec14.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
The document discusses matrix representations of operators and changes of basis in quantum mechanics. Some key points:
- Matrix elements of an operator are computed using a basis of kets. The expectation value of an operator is computed from its matrix elements and the state vectors.
- If two operators commute, they have the same set of eigenkets.
- A change of basis is a unitary transformation that relates two different sets of basis kets that span the same space. It establishes a link between the two basis representations.
- Linear algebra concepts like linear independence of eigenvectors and Hermitian operators having real eigenvalues are important in quantum mechanics.PRODUCT RULES



PRODUCT RULESNumanUsama
Ã˝
This document discusses vector calculus concepts and operations involving the del operator (‚àá). It provides proofs and examples of:
1. Curl of the gradient of a scalar field is equal to zero.
2. The curl of the curl of a vector field is equal to the gradient of the divergence minus the Laplace operator.
3. The curl of the product of a scalar field and a vector field is equal to the scalar field times the curl of the vector field plus the cross product of the gradient of the scalar field and the vector field.
It also defines the Laplace operator and discusses its representation in spherical coordinates.BSC_COMPUTER _SCIENCE_UNIT-2_DISCRETE MATHEMATICS



BSC_COMPUTER _SCIENCE_UNIT-2_DISCRETE MATHEMATICSRai University
Ã˝
This document provides an introduction to definite integration and its applications. It defines indefinite integration as finding the integral or primitive function F(x) of a function f(x). Definite integration involves finding the area under a curve defined by a function f(x) over a specified interval. Standard formulae for integrating common functions like polynomials, trigonometric functions, and exponentials are provided. Methods for integrating functions using substitution and integration by parts are described. Examples of applying these techniques to evaluate definite integrals are also given.Some properties of two-fuzzy Nor med spaces



Some properties of two-fuzzy Nor med spacesIOSR Journals
Ã˝
The study sheds light on the two-fuzzy normed space concentrating on some of their properties like convergence, continuity and the in order to study the relationship between these spacesHERMITE SERIES



HERMITE SERIESMANISH KUMAR
Ã˝
This document discusses Hermite polynomials and their properties. It begins by introducing the Hermite equation, which arises from the theory of the linear harmonic oscillator. The Hermite equation is then solved using a series solution approach. Explicit formulas for the Hermite polynomials Hn(x) are derived for n=0,1,2,3,... using properties of the Hermite equation like recursion relations. Key properties of the Hermite polynomials like generating functions, even/odd behavior, Rodrigue's formula, orthogonality, and recurrence relations are also proved.doc



docSiddharth Pujari
Ã˝
This document is an internship project report submitted by Siddharth Pujari to the Indian Institute of Space Science and Technology. The report focuses on advanced control system design for aircraft and simulating aircraft trajectory. It includes modeling an aircraft's state space model in MATLAB to test controllability. The report also covers theoretical aspects of stability of linear systems, linearizing nonlinear models, controllability of linear systems using the Kalman criterion and transition matrix, and applying these concepts to simulate aircraft controllability in MATLAB.Semana 24 funciones iv √°lgebra uni ccesa007



Semana 24 funciones iv √°lgebra uni ccesa007Demetrio Ccesa Rayme
Ã˝
The document discusses algebra topics including the equality of functions, operations between functions, and function composition. It provides definitions and examples of equal functions, adding, subtracting, multiplying, and dividing functions. Examples are given to demonstrate calculating these operations between functions and finding the domain, range, and graph of the resulting functions.Differential Geometry for Machine Learning



Differential Geometry for Machine LearningSEMINARGROOT
Ã˝
References:
Differential Geometry of Curves and Surfaces, Manfredo P. Do Carmo (2016)
Differential Geometry by Claudio Arezzo
Youtube: https://youtu.be/tKnBj7B2PSg
What is a Manifold?
Youtube: https://youtu.be/CEXSSz0gZI4
Shape analysis (MIT spring 2019) by Justin Solomon
Youtube: https://youtu.be/GEljqHZb30c
Tensor Calculus
Youtube: https://youtu.be/kGXr1SF3WmA
Manifolds: A Gentle Introduction,
Hyperbolic Geometry and Poincaré Embeddings by Brian Keng
Link: http://bjlkeng.github.io/posts/manifolds/,
http://bjlkeng.github.io/posts/hyperbolic-geometry-and-poincare-embeddings/
Statistical Learning models for Manifold-Valued measurements with application to computer vision and neuroimaging by Hyunwoo J.Kim
lec19.ppt



lec19.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
This document discusses finding the eigenvalues and eigenfunctions of a spin-1/2 particle pointing along an arbitrary direction. It shows that the eigenvalue equation reduces to a set of two linear, homogeneous equations. The eigenvalues are found to be ±1/2, and the corresponding eigenvectors are written in terms of the direction angles θ and Φ. As an example, it shows that for a spin oriented along the z-axis, the eigenvectors reduce to simple forms as expected for a spin-1/2 particle. It also introduces the Gauss elimination method for numerically solving systems of linear equations that arise in eigenvalue problems.More from Rai Saheb Bhanwar Singh College Nasrullaganj (20)
lec31.ppt



lec31.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
Complex numbers allow solutions to equations like x2 + 1 = 0 by extending real numbers to include imaginary numbers. A complex number z is defined as z = x + iy, where x and y are real numbers and i is the imaginary unit equal to ‚àö-1. Complex numbers can be added and multiplied following specific rules, such as z1 + z2 = (x1 + x2) + i(y1 + y2) for addition and z1z2 = (x1x2 - y1y2) + i(y1x2 + x1y2) for multiplication. The inverse of a complex number z is calculated as z-1 = (x/(x2+ylec42.ppt



lec42.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) The document discusses examples of calculating the Jacobian of transformations. It defines the Jacobian as the determinant of the partial derivatives of the transformed coordinates.
2) It then discusses Möbius transformations, which are fractional linear transformations of the form (az+b)/(cz+d). The Jacobian of a Möbius transformation depends only on z.
3) Several examples are given of using Möbius transformations to map one geometric region to another, such as mapping a circle to a line.lec41.ppt



lec41.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
This document discusses conformal mapping, which maps curves and regions in such a way that preserves angles and their directions. It provides examples of conformal mappings:
1) The mapping w = ez maps a vertical line in the z-plane to a circle in the w-plane, with the phase angle increasing along the circle.
2) The mapping ω = eiθ0(z-z0)/(z-z0) maps an area in the upper half z-plane to the interior of a unit circle in the ω-plane. Points on the x-axis in z are mapped to the boundary of the circle.lec39.ppt



lec39.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
The document discusses Taylor and Laurent series expansions. It provides examples of using these expansions to represent functions around points.
Taylor series provides a power series representation of an analytic function around a point. Laurent series allows representing functions in annular regions, including points where the function is not analytic, using both positive and negative powers of (z - z0). Examples show deducing Laurent series expansions for simple functions like z4 and 1/z4 around various points, and evaluating coefficients via contour integrals and the residue theorem. The document also gives an example of using a contour integral to compute a Greens function in many-particle physics.lec37.ppt



lec37.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) The document discusses evaluating contour integrals using the residue theorem. It provides examples of calculating residues and evaluating integrals where the contour encloses poles.
2) The residue of a function f(z) at a pole z=a is the coefficient of the (z-a)^-1 term in the Laurent series expansion of f(z) about z=a.
3) According to the residue theorem, the value of a contour integral of a function along a closed loop is equal to 2πi times the sum of the residues of the function enclosed by the contour.lec21.ppt



lec21.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1. The Dirac delta function is an important concept in quantum mechanics and electrodynamics that describes an impulse or large force acting over a very short time interval.
2. The key properties of the Dirac delta function are that it is equal to infinity at a single point and zero everywhere else, and that the integral of the function over its entire range is equal to one.
3. The Dirac delta function can be used to find the value of an arbitrary function f(x) at a specific point a, as the integral of f(x) multiplied by the Dirac delta function over all x is equal to f(a).lec20.ppt



lec20.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
This document contains a series of tutorial problems related to matrices and linear algebra. Problem 1 asks to invert a 3x3 matrix. Problem 2 asks to write a vector as a linear combination of two other vectors. Problem 3 involves finding the inverse, trace, and determinant of related matrices. Problem 4 proves a property about powers of similar matrices. Problem 5 diagonalizes a 2x2 matrix and finds its eigenvalues and eigenvectors.lec18.ppt



lec18.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
This document discusses solving a mass-spring system as an eigenvalue problem. It:
1) Sets up differential equations to model the displacements of two masses connected by springs.
2) Transforms the coupled differential equations into a matrix eigenvalue equation.
3) Solves the eigenvalue equation to obtain the frequencies of oscillation for the two masses.
4) Combines the eigenvectors with complex exponential functions to obtain general solutions for the displacements of each mass over time.lec17.ppt



lec17.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
This document discusses linear transformations and matrices. It introduces how linear transformations on physical quantities are usually described by matrices, where a column vector u representing a physical quantity is transformed into another column vector Au by a transformation matrix A. As an example, it discusses orthogonal transformations, where the transformation matrix A is orthogonal. It proves that for an orthogonal transformation, the inner product of two vectors remains invariant. It also discusses properties of other types of matrices like Hermitian, skew-Hermitian and unitary matrices.lec16.ppt



lec16.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
This document discusses properties of symmetric, skew-symmetric, and orthogonal matrices. It defines each type of matrix and provides examples. Key points include:
- Symmetric matrices have Aij = Aji for all i and j. Skew-symmetric matrices have Aij = -Aji. Orthogonal matrices satisfy AT = A-1.
- The eigenvalues of symmetric matrices are always real. The eigenvalues of skew-symmetric matrices are either zero or purely imaginary.
- Any real square matrix can be written as the sum of a symmetric matrix and skew-symmetric matrix.lec30.ppt



lec30.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) The document discusses calculating the moment of inertia tensor for a cylinder with radius R and height H. It is shown that the only non-zero components of the inertia tensor are Ixx = (3MH + 4MR2)/12, Iyy = Ixx, and Izz = MR2/2.
2) Equations for velocity, acceleration, and the Christoffel symbols in an arbitrary coordinate system are presented. Expressions for calculating acceleration in cylindrical coordinates using the metric tensor and Christoffel symbols are given.lec28.ppt



lec28.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
Tensors obey algebraic properties including addition, multiplication, contraction, and symmetrization. Addition of tensors combines their components. Multiplication of tensors combines their indices and ranks to form a new tensor. Contraction sets equal a covariant and contravariant index, reducing the tensor's rank. Symmetric tensors do not change sign under index interchange, while antisymmetric tensors change sign.lec27.ppt



lec27.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) The document discusses tensors with multiple indices and the cross product of two vectors A and B. The components of the cross product vector C are given by Ai Bj - Aj Bi.
2) It describes how tensor components transform between coordinate systems using transformations of partial derivatives. The transformation property for cross products is derived.
3) Tensors are defined by their rank, with the number of covariant and contravariant indices specifying a tensor's rank. Vectors have a rank of 1. Examples calculate tensor components in different coordinate systems.lec26.ppt



lec26.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) There are two types of vectors - contravariant vectors whose components transform according to Equation 1, and covariant vectors whose components transform according to Equation 2.
2) The dot product of two contravariant or two covariant vectors is not independent of the coordinate system.
3) The dot product of a contravariant and a covariant vector is independent of the coordinate system.lec25.ppt



lec25.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
The document discusses the transformation properties of vectors between two coordinate systems. It states that if a vector has components (x1, x2, x3) in one coordinate system and (xÃÖ1, xÃÖ2, xÃÖ3) in another, there is a relation such that xÃÖi = ai1x1 + ai2x2 + ai3x3, where the aij are the components of the transformation matrix. This relation can be written compactly as xÃÖi = aijxj, using Einstein summation convention. The document then presents two theorems establishing that a set of functions can represent a tensor if their inner product transforms as a tensor under coordinate transformations.lec2.ppt



lec2.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
1) The document discusses the gradient operator and provides examples of calculating the electric field and gradient of functions.
2) It defines the gradient operator mathematically and provides an example of calculating the gradient of a scalar function.
3) Examples are given of using the gradient operator to calculate the electric field from a potential and the gradient of 1/r.lec1.ppt



lec1.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
This document defines vectors and scalar quantities, and describes their key properties and relationships. It begins by defining physical quantities that can be measured, and distinguishes between scalar and vector quantities. Scalars have only magnitude, while vectors have both magnitude and direction. The document then provides a more rigorous definition of vectors as quantities that remain invariant under coordinate system rotations or translations. It describes how to represent and transform vectors between different coordinate systems. Vector addition, subtraction, and multiplication operations like the scalar and vector products are defined. Derivatives of vectors are also discussed. Examples of velocity and acceleration vectors in uniform circular motion are provided.lec15.ppt



lec15.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
The rank of a matrix is the maximum number of linearly independent rows. A matrix has rank 0 only if it is the zero matrix. The inverse of a matrix A, denoted A^-1, is defined such that A*A^-1 = I, the identity matrix. To calculate the inverse, one takes the transpose of the cofactor matrix and divides each element by the determinant of the original matrix.lec13.ppt



lec13.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
A Hilbert space is an infinite-dimensional vector space consisting of sequences of real numbers that satisfy a convergence condition. It allows vector addition and scalar multiplication. In quantum mechanics, state vectors span a Hilbert space. For identical particles, boson state vectors are symmetric and fermion state vectors are antisymmetric. Linear algebra concepts like operators, eigenvectors, and superposition are used in Dirac's formulation of quantum mechanics postulates. Observables are represented by operators and eigenvectors correspond to eigenvalues. Any state can be written as a superposition of eigenvectors.lec11.ppt



lec11.pptRai Saheb Bhanwar Singh College Nasrullaganj
Ã˝
The document discusses the Gram-Schmidt orthogonalization (GSO) process for constructing an orthonormal basis from a set of linearly independent vectors. It explains that GSO works by taking a vector, normalizing it to unit length to create the first basis vector, then subtracting the component of the next vector along this first vector to make it orthogonal, and repeating this process to iteratively construct an orthonormal basis. An example applies GSO to three vectors in R3, finding the orthonormal basis vectors by removing components along each preceding vector at each step.Recently uploaded (20)
How to create security group category in Odoo 17



How to create security group category in Odoo 17Celine George
Ã˝
This slide will represent the creation of security group category in odoo 17. Security groups are essential for managing user access and permissions across different modules. Creating a security group category helps to organize related user groups and streamline permission settings within a specific module or functionality.Azure Administrator Interview Questions By ScholarHat



Azure Administrator Interview Questions By ScholarHatScholarhat
Ã˝
Azure Administrator Interview Questions By ScholarHatOral exam Kenneth Bech - What is the meaning of strategic fit?



Oral exam Kenneth Bech - What is the meaning of strategic fit?MIPLM
Ã˝
Presentation of the CEIPI DU IPBA oral exam of Kenneth Bech - What is the meaning of strategic fit? Mastering Soft Tissue Therapy & Sports Taping



Mastering Soft Tissue Therapy & Sports TapingKusal Goonewardena
Ã˝
Mastering Soft Tissue Therapy & Sports Taping: Pathway to Sports Medicine Excellence
This presentation was delivered in Colombo, Sri Lanka, at the Institute of Sports Medicine to an audience of sports physiotherapists, exercise scientists, athletic trainers, and healthcare professionals. Led by Kusal Goonewardena (PhD Candidate - Muscle Fatigue, APA Titled Sports & Exercise Physiotherapist) and Gayath Jayasinghe (Sports Scientist), the session provided comprehensive training on soft tissue assessment, treatment techniques, and essential sports taping methods.
Key topics covered:
✅ Soft Tissue Therapy – The science behind muscle, fascia, and joint assessment for optimal treatment outcomes.
✅ Sports Taping Techniques – Practical applications for injury prevention and rehabilitation, including ankle, knee, shoulder, thoracic, and cervical spine taping.
✅ Sports Trainer Level 1 Course by Sports Medicine Australia – A gateway to professional development, career opportunities, and working in Australia.
This training mirrors the Elite Akademy Sports Medicine standards, ensuring evidence-based approaches to injury management and athlete care.
If you are a sports professional looking to enhance your clinical skills and open doors to global opportunities, this presentation is for you.ASP.NET Web API Interview Questions By Scholarhat



ASP.NET Web API Interview Questions By ScholarhatScholarhat
Ã˝
ASP.NET Web API Interview Questions By ScholarhatAzure Data Engineer Interview Questions By ScholarHat



Azure Data Engineer Interview Questions By ScholarHatScholarhat
Ã˝
Azure Data Engineer Interview Questions By ScholarHatAI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
Ã˝
AI and Academic Writing, Short Term Course in Academic Writing and Publication, UGC-MMTTC, MANUU, 25/02/2025, Prof. (Dr.) Vinod Kumar Kanvaria, University of Delhi, vinodpr111@gmail.comIntellectual Honesty & Research Integrity.pptx



Intellectual Honesty & Research Integrity.pptxNidhiSharma495177
Ã˝
Research Publication & Ethics contains a chapter on Intellectual Honesty and Research Integrity.
Different case studies of intellectual dishonesty and integrity were discussed.Meeting the needs of modern students?, Selina McCoy



Meeting the needs of modern students?, Selina McCoyEconomic and Social Research Institute
Ã˝
NAPD Annual Symposium
“Equity in our Schools: Does the system deliver for all young people?”Effective Product Variant Management in Odoo 18



Effective Product Variant Management in Odoo 18Celine George
Ã˝
In this slide we’ll discuss on the effective product variant management in Odoo 18. Odoo concentrates on managing product variations and offers a distinct area for doing so. Product variants provide unique characteristics like size and color to single products, which can be managed at the product template level for all attributes and variants or at the variant level for individual variants.BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAH



BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAHcoacharyasetiyaki
Ã˝
BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAHInterim Guidelines for PMES-DM-17-2025-PPT.pptx



Interim Guidelines for PMES-DM-17-2025-PPT.pptxsirjeromemanansala
Ã˝
This is the latest issuance on PMES as replacement of RPMS. Kindly message me to gain full access of the presentation. NUTRITIONAL ASSESSMENT AND EDUCATION - 5TH SEM.pdf



NUTRITIONAL ASSESSMENT AND EDUCATION - 5TH SEM.pdfDolisha Warbi
Ã˝
NUTRITIONAL ASSESSMENT AND EDUCATION, Introduction, definition, types - macronutrient and micronutrient, food pyramid, meal planning, nutritional assessment of individual, family and community by using appropriate method, nutrition education, nutritional rehabilitation, nutritional deficiency disorder, law/policies regarding nutrition in India, food hygiene, food fortification, food handling and storage, food preservation, food preparation, food purchase, food consumption, food borne diseases, food poisoningHow to Configure Proforma Invoice in Odoo 18 Sales



How to Configure Proforma Invoice in Odoo 18 SalesCeline George
Ã˝
In this slide, we’ll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.Administrative bodies( D and C Act, 1940



Administrative bodies( D and C Act, 1940P.N.DESHMUKH
Ã˝
These presentation include information about administrative bodies such as D.T.A.B
CDL AND DCC, etc.AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
Ã˝
lec33.ppt
- 1. NPTEL ‚Äì Physics ‚Äì Mathematical Physics - 1 Lecture 33 Cauchy Riemann (CR) conditions CR conditions state that a necessary and a sufficient condition that a function, ùëì(ùëß) defined as, ùëì(ùëß) = ùë¢(ùë•, ùë¶) + ùëñùë£(ùë•, ùë¶) be analytic in a region ÔÉÇ provides the following conditions (called CR conditions) on the partial derivatives of ùë¢ ùëéùëõùëë ùë£ are met, ùúïùë¢ = ùúïùë£ and ùúïùë¢ = ‚àí ùúïùë£ ùúïùë• ùúïùë¶ ùúïùë¶ ùúïùë• in ÔÉÇ. Additionally it is assumed that the partial derivatives are continuous in ÔÉÇ. To arrive at the proof of the above equations, let us look at the necessary conditions. For a function ùëì(ùëß) to be analytic, it should be differentiable in a region ÔÉÇ, that is ùêøùëñùëö ‚àÜùëß ‚Üí 0 ùëì(ùëß+‚àÜ(ùëß)‚àíùëì(ùëß) ‚àÜùëß = ùëì‚Ä≤ (ùëß) ùë¢(ùë• + ‚àÜùë•, ùë¶ + ‚àÜùë¶) + ùëñùë£ (ùë• + ‚àÜùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶) + ùëñùë£(ùë•, ùë¶) ‚àÜùë• + ùëñ‚àÜùë¶ ‚àÜùë•‚Üí0 ùêøùëñùëö ‚àÜù붂Üí0 ùêøùëñùëö must exist and should be independent of the manner in ‚àÜùëß approaches zero. Two possibilities are apparent for that to happen. Case A ‚àÜùë¶ = 0, ‚àÜùë• ‚Üí 0 For which ùëì‚Ä≤(ùëß) is defined as, ùëì‚Ä≤(ùëß) = ‚àÜùë•‚Üí0 ùêøùë° ùë¢(ùë• + ‚àÜùë•, ùë¶) ‚àí ùë¢(ùë•, ùë¶) ‚àÜùë• + ùëñ [ ùë£(ùë• + ‚àÜùë•, ùë¶)ùë£(ùë•, ùë¶) ‚àÜùë• ] = + ùëñ ùúïùë¢ ùúïùë£ ùúïùë• ùúïùë• Assuming that the partial derivatives exist. Joint initiative of IITs and IISc ‚Äì Funded by MHRD Page 12 of 66
- 2. NPTEL ‚Äì Physics ‚Äì Mathematical Physics - 1 Case B ‚àÜùë¶ ‚Üí 0, ‚àÜùë• = 0 In this case, ùëì‚Ä≤(ùëß) = ‚àÜù붂Üí0 ùêøùëñùëö ùë¢(ùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶) ùëñ‚àÜùë• + ùë£(ùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë£(ùë•, ùë¶) ‚àÜùë¶ = ùúïùë¢ + ùëñùúïùë£ ùúïùë¶ ùúïùë¶ Of course, these two cases will have to yield identical results. Thus ùúïùë¢ ùúïùë£ ùúïùë• + ùëñ ùúïùë• ùúïùë¢ ùúïùë£ = ‚àíùëñ ùúï ùë¶ + ùúïùë¶ Or, = ùúïùë¢ ùúïùë£ ùúïùë• ùúïùë¶ ùúïùë• and = ‚àíùëñ ùúïùë£ ùúïùë¢ ùúïùë¶ Next we look at the sufficiency conditions. Since and ùúïùë¢ ùúïùë• ùúïùë¢ ùúïùë¶ are assumed to be continuous, we have ‚àÜùë¢ = ùë¢(ùë• + ‚àÜùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶) = [ùë¢(ùë• + ‚àÜùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶ + ‚àÜùë¶)] + [ùë¢(ùë•, ùë¶ + ‚àÜùë¶) ‚àí ùë¢(ùë•, ùë¶)] Where the second and third terms are subtracted and added. Hence ‚àÜùë¢ = ùúïùë¢ ‚àÜùë• + ùúïùë¢ ‚àÜùë¶ ùúïùë• ùúïùë¶ Similarly ‚àÜùë£ = ùúïùë£ ‚àÜùë• + ùúïùë£ ‚àÜùë¶ ùúïùë• ùúïùë¶ Thus ‚àÜùë§ = ‚àÜùë¢ + ùëñ‚àÜùë£ = ( + ùëñ ) ‚àÜùë• + ( ùúïùë¢ ùúïùë• ùúïùë¶ ùúïùë£ ùúïùë¢ ùúïùë¶ + ùëñ ) ‚àÜùë¶ ùúïùë£ ùúïùë¶ Changing the second bracket using CR conditions ‚àÜùë§ = ( + ùëñ ) ‚àÜùë• + (‚àí + ùëñ ) ‚àÜùë¶ ùúïùë¢ ùúïùë£ ùúïùë• ùúïùë• ùúïùë• ùúïùë• ùúïùë£ ùúïùë¢ = ( + ùëñ ) (ùë• + ùëñ‚àÜùë¶) Joint initiative of IITs and IISc ‚Äì Funded by MHRD Page 13 of 66 ùúïùë¢ ùúïùë£ ùúïùë• ùúïùë•
- 3. NPTEL ‚Äì Physics ‚Äì Mathematical Physics - 1 = ( + ùëñ ) ‚àÜùëß ùúïùë¢ ùúïùë£ ùúïùë• ùúïùë¶ Hence ùêøùëñùëö‚àÜùë§ ‚àÜùëß‚Üí0 ‚àÜ ùëß = ùëëùë§ = ùëì‚Ä≤(ùëß) = ùúïùë¢ + ùëñ ùúïùë£ ùëëùëß ùúïùë• ùúï ùë• proving that the derivative exists and so ùëì(ùëß) is analytic ÔÉÇ. Examples 1. ùëì(ùëß) = ùëß2 = ùë•2 ‚àí ùë¶2 + ùëñ2ùë•ùë¶ ùëì‚Ä≤(ùëß) = 2ùëß To verify CR condition, ùë¢(ùë•, ùë¶) = ùë•2 ‚àí ùë¶2 ùë£(ùë•, ùë¶) = 2ùë•ùë¶ ùë¢ùë• = 2ùë• = ùë£ùë¶ , ùë¢ùë¶ = ‚àí2ùë¶ = ‚àíùë£ùë• ùëì‚Ä≤(ùëß) = 2ùë• + ùëñ2ùë¶ = 2ùëß (where the suffix refers to the derivative taken with respect to that variable). 2. ùëì(ùëß) = |ùëß|2, ùë¢(ùë•, ùë¶) = ùë•2 + ùë¶2, ùë£(ùë•, ùë¶) = 0 If the CR conditions hold at a point (ùë•, ùë¶) then the point would be, 2ùë• = 0, 2ùë¶ = 0 ‚áí (ùë•, ùë¶) = (0,0). So ùëì‚Ä≤(ùëß) does not exist at a non-zero point. Exercise: Check for the analyticity of the following functions. ùëì(ùëß) = ùëñ|ùëß|3 |ùëß| = ‚àöùë•2 + ùë¶2 |ùëß|3 = (ùë•2 + ùë¶2)2 3 3 ùëì(ùëß) = ùëñ(ùë•2 + ùë¶2)2 3 ùë¢(ùë•, ùë¶) = 0, ùë£(ùë•, ùë¶) = ùëñ(ùë•2 + ùë¶2)2 It is a purely complex function. It‚Äôs differentiable only at the origin and hence not an analytic function. Joint initiative of IITs and IISc ‚Äì Funded by MHRD Page 14 of 66
- 4. Joint initiative of IITs and IISc ‚Äì Funded by MHRD Page 15 of 66 NPTEL ‚Äì Physics ‚Äì Mathematical Physics - 1 Second Theorem Sufficient condition for differentiability Let the function ùëì(ùëß) = ùë¢(ùë•, ùë¶) + ùëñùë£(ùë•, ùë¶) be defined throughout some ‚Ñá neighborhood of a point ùëß0 = ùë•0 + ùëñùë¶0 and suppose that the first-order partial derivatives of the functions ùë¢ and ùë£ with respect to ùë• and ùë¶ exist everywhere in that neighborhood. If those partial derivatives are continuous at (ùë•0, ùë¶0) and satisfy CR conditions, then ùë¢ùë• = ùë£ùë¶, ùë¢ùë¶ = ‚àíùë£ùë• at (ùë•0, ùë¶0) then ùëì‚Ä≤(ùë•0, ùë¶0) (= f ÔÇ¢ (ùëß0)) exists. ùë¢ùë• = ùë£ùë¶, ùë£ùë• = ‚àíùë¢ùë¶ should necessarily be satisfied if ùëì(ùëß) has a derivative at a point z. Thus it is the necessary and sufficient condition that must hold if ùëì(ùëß) is differentiable. If they hold, then ùëì‚Ä≤(ùëß) exists and is given by, ùëì‚Ä≤(ùëß) = ùë¢ùë•(ùë•, ùë¶) + ùëñùë£ùë•(ùë•, ùë¶) ùëì‚Ä≤(ùëß) = ‚àíùëñùë¢ùë¶(ùë•, ùë¶) + ùë£ùë¶(ùë•, ùë¶)





