![モデル式の記述
モデル式5-3
? ? = ?1 + ?2 ? ? + ?3 ????? ? ? = 1, … , ?
? ? ~?????? ?[?], ? ? = 1, … , ?
11
Yの予測値*はAとScoreの線形結合で決定する
予測値*を中心に標準偏差?の正規分布
に従うノイズがのって、Yの値が決まる
*ここでは予測値を一つの値の指すものとして使っており、本書とは異なる意味で使ってます。
本書では予測値は予測分布のとりうる値を指します。](https://image.slidesharecdn.com/osaka-161223162916/85/Osaka-stan-2-chap5-1-11-320.jpg)
![モデル式5-2(再)
? ? ~?????? ?[?], ?
? ? = ?1 + ?2 ? ? + ?3 ????? ? ? = 1, … , ?
12
Yは正規分布から発生している
正規分布の平均パラメタは、説明変数の線形結合で表現され
る
? ? ~?????? ?1 + ?2 ? ? + ?3 ????? ? , ? ? = 1, … , ?
?平均パラメタを代入してやればモデル式5-2](https://image.slidesharecdn.com/osaka-161223162916/85/Osaka-stan-2-chap5-1-12-320.jpg)
![Stanで実装
13
(再) モデル式5-3
? ? = ?1 + ?2 ? ? + ?3 ????? ? ? = 1, … ?
? ? ~?????? ?[?], ? ? = 1, … , ?
そのまま
model5-3.stan
←Scoreは200点満点だったが、
0-1の範囲で指定されている
←のちにベイズ予測区間を描くので、
予測分布からのMCMCサンプルを生成](https://image.slidesharecdn.com/osaka-161223162916/85/Osaka-stan-2-chap5-1-13-320.jpg)
![推定結果の解釈
得られた事後平均をモデル式に代入すると
回帰係数は「説明変数が1増えたときのyの平均的な変化量」
15
収束している模
様
? ? = 0.13 ? 0.14 ? ? ? + 0.32 ?
????? ?
200
? = 1, … , ?
? ? ~?????? ?[?], 0.05 ? = 1, … , ?](https://image.slidesharecdn.com/osaka-161223162916/85/Osaka-stan-2-chap5-1-15-320.jpg)
![パラメタの幅の確認
分布でしょ！
19
95%ベイズ信頼区間
[0.06~0.19] [-0.17~-0.11]
[0.22~0.42] [0.04~0.06]](https://image.slidesharecdn.com/osaka-161223162916/85/Osaka-stan-2-chap5-1-19-320.jpg)
![まとめ
重回帰: 複数の変数で応答変数を予測する
モデル:
交互作用→Chap7.1
多重共線性→Chap7.4
24
? ? ~?????? ?[?], ?
? ? = ?0 + ?1 ?1 + ?2 ?2 + ? + ? ? ? ?
1)Yは正規分布から発生している
2) 正規分布の平均パラメタは、
説明変数の線形結合で表現される](https://image.slidesharecdn.com/osaka-161223162916/85/Osaka-stan-2-chap5-1-24-320.jpg)
Osaka.stan#2 chap5-1
- 2. 重回帰 (multiple linear regression) ?目的変数を複数の説明変数で予測する →回帰分析の説明変数が複数になっただけ 2 ? ?2 ?1
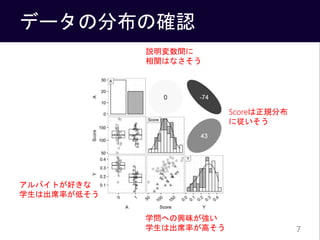
- 3. 本書で扱うデータ 出欠率に関する架空データ (n = 50) A: アルバイトが好きかどうかの2値 (好き = 1) Score: 学問への興味の強さ (200点満点) Y: 1年間の出欠率 (出席回数 / 総授業回数) * 総授業回数は200~500(人によって異なる) 3
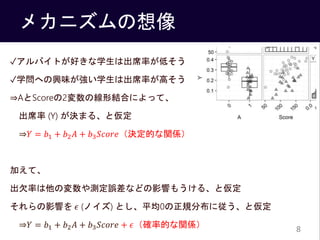
- 8. メカニズムの想像 ?アルバイトが好きな学生は出席率が低そう ?学問への興味が強い学生は出席率が高そう ?AとScoreの2変数の線形結合によって、 出席率 (Y) が決まる、と仮定 ?? = ?1 + ?2 ? + ?3 ?????（決定的な関係） 加えて、 出欠率は他の変数や測定誤差などの影響もうける、と仮定 それらの影響を ? (ノイズ) とし、平均0の正規分布に従う、と仮定 ?? = ?1 + ?2 ? + ?3 ????? + ?（確率的な関係） 8
- 9. モデル式の記述 モデル式5-1 ? ? = ?1 + ?2 ? ? + ?3 ????? ? + ? ? ? = 1, … , ? ? ? ~?????? 0, ? ? = 1, … , ? 9 AとScoreの線形結合 ノイズ ノイズは平均0, 標準偏差? の正規分布従う
- 10. モデル式の記述 モデル式5-2 ( ? を消去) ? ? ~?????? ?1 + ?2 ? ? + ?3 ????? ? , ? ? = 1, … , ? 10 (再) モデル式5-1 ? ? = ?1 + ?2 ? ? + ?3 ????? ? + ? ? ? = 1, … , ? ? ? ~?????? 0, ? ? = 1, … , ?
- 11. モデル式の記述 モデル式5-3 ? ? = ?1 + ?2 ? ? + ?3 ????? ? ? = 1, … , ? ? ? ~?????? ?[?], ? ? = 1, … , ? 11 Yの予測値*はAとScoreの線形結合で決定する 予測値*を中心に標準偏差?の正規分布 に従うノイズがのって、Yの値が決まる *ここでは予測値を一つの値の指すものとして使っており、本書とは異なる意味で使ってます。 本書では予測値は予測分布のとりうる値を指します。
- 12. モデル式5-2(再) ? ? ~?????? ?[?], ? ? ? = ?1 + ?2 ? ? + ?3 ????? ? ? = 1, … , ? 12 Yは正規分布から発生している 正規分布の平均パラメタは、説明変数の線形結合で表現され る ? ? ~?????? ?1 + ?2 ? ? + ?3 ????? ? , ? ? = 1, … , ? ?平均パラメタを代入してやればモデル式5-2
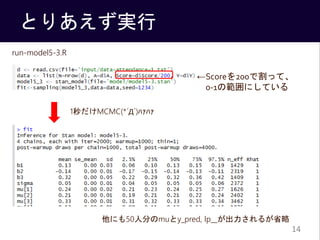
- 13. Stanで実装 13 (再) モデル式5-3 ? ? = ?1 + ?2 ? ? + ?3 ????? ? ? = 1, … ? ? ? ~?????? ?[?], ? ? = 1, … , ? そのまま model5-3.stan ←Scoreは200点満点だったが、 0-1の範囲で指定されている ←のちにベイズ予測区間を描くので、 予測分布からのMCMCサンプルを生成
- 15. 推定結果の解釈 得られた事後平均をモデル式に代入すると 回帰係数は「説明変数が1増えたときのyの平均的な変化量」 15 収束している模 様 ? ? = 0.13 ? 0.14 ? ? ? + 0.32 ? ????? ? 200 ? = 1, … , ? ? ? ~?????? ?[?], 0.05 ? = 1, … , ?
- 18. 外挿について 外挿: データ範囲の外側を予測すること アルバイト好きでScoreが0点の学生の出席率は？ 0.13 ? 0.14 ? 1 + 0.32 ? 0 200 = ?0.01 18 ? ? = 0.13 ? 0.14 ? ? ? + 0.32 ? ????? ? 200 ? = 1, … , ? ? ? ~?????? ? ? , 0.05 ? = 1, … , ? 出席率が負？ データの範囲外の値について の予測はしない方がよい
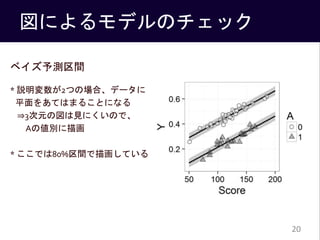
- 20. 図によるモデルのチェック ベイズ予測区間 * 説明変数が2つの場合、データに 平面をあてはまることになる ?3次元の図は見にくいので、 Aの値別に描画 * ここでは80%区間で描画している 20
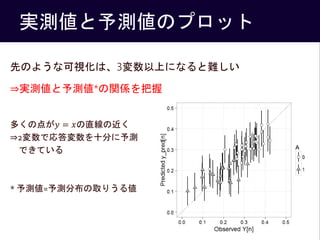
- 21. 実測値と予測値のプロット 先のような可視化は、3変数以上になると難しい ?実測値と予測値*の関係を把握 多くの点が? = ?の直線の近く ?2変数で応答変数を十分に予測 できている * 予測値=予測分布の取りうる値 21
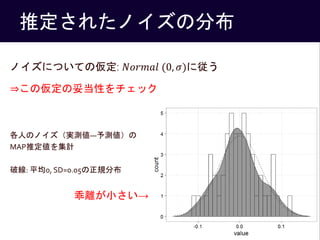
- 22. 推定されたノイズの分布 ノイズについての仮定: ?????? (0, ?)に従う ?この仮定の妥当性をチェック 各人のノイズ（実測値―予測値）の MAP推定値を集計 破線: 平均0, SD=0.05の正規分布 乖離が小さい→ 22
- 24. まとめ 重回帰: 複数の変数で応答変数を予測する モデル: 交互作用→Chap7.1 多重共線性→Chap7.4 24 ? ? ~?????? ?[?], ? ? ? = ?0 + ?1 ?1 + ?2 ?2 + ? + ? ? ? ? 1)Yは正規分布から発生している 2) 正規分布の平均パラメタは、 説明変数の線形結合で表現される
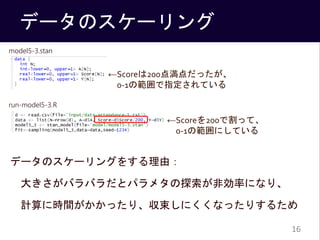
- 26. 架空データの作り方 架空データを自分で作って(*?Д`)????する （真値がわかっているので、モデルの性質を把握しやすい） 26 rnorm(): 正規分布に従う乱数を発生 Cf. モデル式 ? ? = ?0 + ?1 ?1 + ?2 ?2 + ? ? ? ? ~?????? 0, ? 同じ lm()で分析すると↓ ←平均3, 標準偏差1の 正規分布に従う乱数を100個発生
- 27. Stanで推定 27 モデル (modelブロックのみ) 実行コード Cf. 発生させたデータ パラメタの真値は ?0 = 3, ?1 = 2, ?2 = 5, ? = 2.5 うまく推定できている ←パラメタについて 弱情報事前分布を設定
- 28. ノイズの大きさをいじってみる 28 ? = 0.5 ? = 10 cf. ? = 3 実測値と予測値が 対応しにくくなる パラメタのベイズ信頼区間は ノイズが大きくなると広がる * 事後平均値はlm()と一致する ノイズが大きいと乱数の発生毎に 係数は大きく変化
Editor's Notes
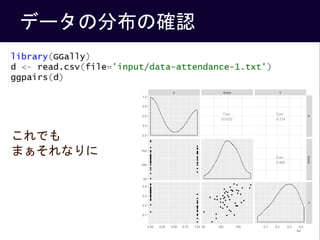
- #4: 率だから二項分布でモデリングしないと、思われる方もいるかもしれない 分母にあたる授業回数(2項分布でいうN試行数)が多ければ、正規分布で十分近似できるので、このデータで重回帰する。 二項分布をもちいたモデリングについては、次回。
- #8: Ｙの分布についての読み取りがないのは何か理由がある？ 逆になぜScoreについての読み取りがあるのか
- #10: 心理统计的な书き方に近い
- #12: Muについて、心理統計の本ではyの予測値yhutという言い方をしている その言い方でいえば、 Yの予測値はAとScoreの線形結合で決定する 予測値を中心に標準偏差?の正規分布に従うノイズがのって、Yの値が決まる 本書では予測値は予測分布のとりうる値（MCMCサンプル）を指します。
- #13: モデル5-3の①と②を逆転して
- #14: データの範囲を指定していた方がよい？ 予測分布からのMCMCサンプリング
- #16: アルバイトが好きな学生(1)はそうでない学生(0)に比べて、出席率が平均的に0.14低い Scoreは0~200点が0~1に変換されているので、0点の学生は200点の学生に比べて出席率が平均的に0.32高い、ということ。 150点の学生は50点の学生に比べて、出席率が平均的に0.16高い
- #17: パラメタの大きさを1程度にそろえる、とある。 パラメタ？
- #18: モデルはデータブロックでScoreの範囲についての部分を削除している。 Scoreのデータを200で割らずにわたす
- #19: 本では「出席率のベースライン尘耻」といういいかた
- #20: パラメタの値が0より大きい（または小さい）確率を伝統的な統計学における回帰係数の有意性判定になぞらえてBayesian p-valueと呼ぶ流儀もある
- #21: これまで95%で描画してきたのは伝統的な統計学を意識してのこと 解析者が適宜区間を変えてよいという立場。 この章の解析においては8割の確率で予測を当てれば十分だ、という意向で80％区間
- #22: 「80%区間が直線を含んでいる」というのは十分に予測できている根拠になる？ データ数が少ないなどで、80％区間が広がることもある、のでは ここでの予測値は、予測
- #23: ここでの予测値は惭颁惭颁サンプルであって、特定の値ではない。
- #24: 厂辫别补谤尘补苍の顺位相関係数×100
- #28: 教科書ではtransformed parametersで書いてるけど、モデルブロックでmuを書くこともできる。 書き方の一例として。(ただしgene quaで使えなくなるので、予測区間を書いたりするための予測分布からのMCMCサンプリングを出すときには、transformed paraで書く必要） パラメタの弱情報事前分布として、それぞれ設定。 Sigmaはパラメタの下限を0にしている。ハーフコーシー。 推定はうまくいっているが、乱数依存のところがある。
- #29: 事后平均値は濒尘と一致するが、パラメタのベイズ信頼区间はノイズが大きいと広がる
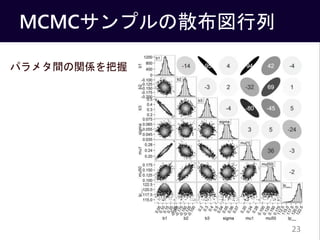
- #30: 回帰係数パラメタの相関
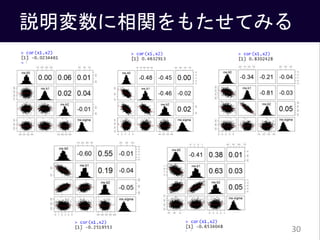
- #31: 説明変数の相関をいれると推定にちょっと时间がかかる