笔搁惭尝第3章冲3.3-3.4
- 2. - 2 - 第3章 線形回帰モデル ? 3.3 ベイズ線形回帰 ? 3.3.1 パラメータの分布 ? 3.3.2 予測分布 ? 3.3.3 等価カーネル ? 3.4 ベイズモデル比較 ? 3.5 エビデンス近似 ? 3.5.1 エビデンス関数の評価 ? 3.5.2 エビデンス関数の最大化 ? 3.5.3 有効パラメータ数 ? 3.6 固定された基底関数の限界 ここまで
- 3. - 3 - 3.3 ベイズ線形回帰 ? 今までの内容で分かったこと(最尤推定の場合) ? 基底関数の数によって決まるモデルの複雑さをデータサイズに応じて 決定する必要性 ? 正則化項(Lasso, Ridge etc)を追加することによって、モデルの複雑さ を調整可能(基底関数の数と形を選ぶことは正則化を付けても重要) ? 解こうとしている問題に合わせてモデルの複雑さを決める必要 ? 尤度最大化では、常に複雑なモデルを選択する危険性(過学習) ? 過学習への対処 ? クロスバリデーション 学習、評価、テストの3つに分割するのが一般的。以下手順。 ①[学習, 評価]の組み合わせをkに分割し、 k-1個のデータで学習、1個で評価。入れ替えながらハイパラ探索。 ②ベスパラで[学習, 評価]データ全てを学習し、1つのモデルを作成。 ③テストデータで性能評価。 ? これを複数モデルで実施して、テストデータでの評価結果を比較 (計算量が多い)。手元にある一部のデータを学習に使えない。
- 4. - 4 - 3.3 ベイズ線形回帰 ? 3.3~3.6節のモチベーション ? 教師データ全てを使って、線形回帰モデルをベイズ的に扱うと ともに、モデルの複雑さを自動的に決定したい。 ? P164によると、テスト用の独立なデータは取っておいた方が賢 明とのこと。
- 5. - 5 - 3.3.1 パラメータの分布 ? モデルパラメータwの推定 ? モデルパラメータwの事前分布を導入し、線形回帰モデルを ベイズ的に扱う。 事前分布(3.48):p w = ? ? ?0, ?0 尤度関数(3.10):p(t|X, w, β) = Π ?=0 ? ?(? ?|? ?φ ? ? , β?1) 事後分布(3.49):p w t ∝ p t X, w, β ? w = ?(?|? ?, ? ?) ※演習3.7 ただし、 平均(3.50):? ? = ? ? ? ? ?1 ?0 + βΦ ? ? 分散共分散(3.51):S ? ?1 = ?0 ?1 + βΦ ? Φ 計画行列(3.16) :Φ = φ0 ?1 ? φ ??1(?1) ? ? ? φ0(? ?) ? φ ??1(? ?) 基底関数:φ ? = φ ? ? = (φ0 ? ? , φ1 ? ? , ‥φ ??1 ? ? ) ? ※(m,m)((m,m)(m,1)+(m,n)(n,1))=(m,1) ※(m,m)+(m,n)(n,m)=(m,m) ※(n,m) ※(m,1)
- 6. - 6 - 演習3.7
- 7. - 7 - 演習3.7
- 8. - 8 - ? モデルパラメータwの推定(続き) 平均(3.50):? ? = ? ? ? ? ?1 ?0 + βΦ ? ? 分散共分散(3.51):S ? ?1 = ?0 ?1 + βΦ ? Φ ? 事前分布を単一の精度パラメータαとし、期待値=0のガウスを考 える(αとβは既知)。 事前分布(3.52):p(w|α) = ? ? 0, α?1 ? 事後分布(3.49):p w t ∝ p(t|X, w, β)P w|α = ?(?|? ?, ? ?) ただし、 平均(3.53):? ? = β? ?Φ ? ? 分散共分散(3.54):S ? ?1 = α? + βΦ ?Φ ? 事後分布の対数を取ったものをwに関して最大化すればwの推定 が可能 事後分布(3.55):ln p w t = ? β 2 σ ?=1 ? {? ? ? ? ? φ(? ?)}2 ? α 2 ? ? ? + 定数 3.3.1 パラメータの分布 二乗和誤差 正則化項
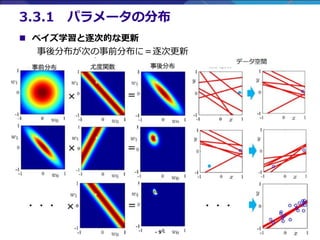
- 9. - 9 - ? ベイズ学習と逐次的な更新 事後分布が次の事前分布に=逐次更新 3.3.1 パラメータの分布
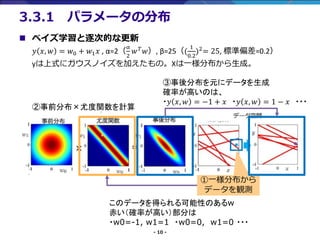
- 10. - 10 - 3.3.1 パラメータの分布 ①一様分布から データを観測 このデータを得られる可能性のあるw 赤い(確率が高い)部分は ?w0=-1, w1=1 ?w0=0, w1=0 ??? ③事後分布を元にデータを生成 確率が高いのは、 ?? ?, ? = ?1 + ? ?? ?, ? = 1 ? ? ??? ②事前分布×尤度関数を計算 ? ベイズ学習と逐次的な更新 ? ?, ? = ?0 + ?1 ? , α=2( α 2 ? ? ?), β=25(( 1 0.2 )2 = 25, 標準偏差=0.2) yは上式にガウスノイズを加えたもの。Xは一様分布から生成。
- 11. - 11 - ? 新たなデータ ? に対応する ? の予測 ? 3.3.1では?の分布を求めたが、実際は ? の予測を行いたい。 予測分布(3.57):p(t|?, ?, ?, α, β) = ??? ? ? ?, ?, β ? ? ?, ?, α, β ?? ? 予測分布(3.58):p t ?, ?, ?, α, β = ? ? ? ? ? φ ? , σ ? 2 ? ただし、 分散(3.59):σ ? 2 ? = 1 β + φ(?)?1 ? ?φ(x) 平均(3.53):? ? = β? ?Φ ? ? 分散共分散(3.54):S ? ?1 = α? + βΦ ? Φ ? (3.59)式の第1項はデータに含まれるノイズ、第2項は?の不確かさ(分散 が大きい=データが散らばっており、 ?の推定値が不確か)を表す。 ? 新しいデータを観測すると事後分布は必ず狭くなる。 ? N→∞で分散(第2項) が0に収束するため予測分布の分散はβのみに依存。 3.3.2 予測分布 求めたwの確率と 新しいxでtの確率を算出 教師データ(X,T)及び既知の α,βでwの確率を算出
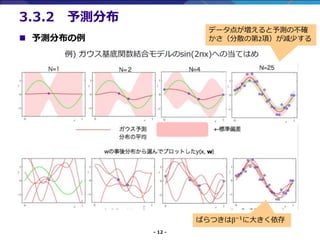
- 12. - 12 - ? 予測分布の例 3.3.2 予測分布 データ点が増えると予測の不確 かさ(分散の第2項)が減少する ばらつきはβ?1 に大きく依存
- 13. - 13 - ? カーネル法の導入 ? 式の導出 (3.3)式に(3.53)式を代入 予測分布の平均(3.60):? ?, ? ? = ? ? ? φ ? = βφ(?) ? ? ?Φ ? ? = σ ?=1 ? βφ ? ? ? ?φ(? ?)? ? ここで、 等価カーネル※(3.62) :? ?, ?′ = βφ ? ? ? ?φ(?′) とおくと、以下の形になる。 予測分布の平均(3.60):? ?, ? ? = σ ?=1 ? ? ?, ? ? ? ? ただし、 予測分布(3.3):y(x, w) = σ ?=1 ??1 ??φ ? ? = ? ? φ(?) 平均(3.53) :? ? = β? ?Φ ? ? 分散共分散(3.54):S ? ?1 = α? + βΦ ? Φ 3.3.3 等価カーネル ※(1,m)(m,m)(m,1)=(1,1) ※平滑化行列とも呼ぶ 予測したいデータのx 訓練データ 計算結果が(1,1)になれば良い。 ? ?Φ ? ? = (?, 1)なので、 φ(?) ? = (1, ?)を前に置けば (1,1)になる。
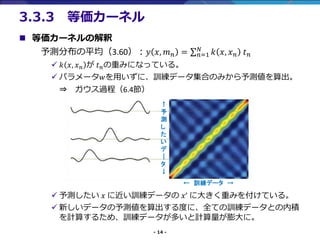
- 14. - 14 - ? 等価カーネルの解釈 予測分布の平均(3.60):? ?, ? ? = σ ?=1 ? ? ?, ? ? ? ? ? ? ?, ? ? が ? ?の重みになっている。 ? パラメータ?を用いずに、訓練データ集合のみから予測値を算出。 ? ガウス過程(6.4節) ? 予測したい ? に近い訓練データの ?’ に大きく重みを付けている。 ? 新しいデータの予測値を算出する度に、全ての訓練データとの内積 を計算するため、訓練データが多いと計算量が膨大に。 3.3.3 等価カーネル ← 訓練データ → ↑ 予 測 し た い デ | タ ↓
- 15. - 15 - ? 本節のモチベーション ? モデル選択をベイズ的に行いたい。 ? モデルの不確かさを表すために確率を用いる。 教師データは何らかのモデルから生成されているとする。 ただし、どのモデルから生成されたかは分からない。 ? 最も教師データを生成したと考えられるモデル (多項式?ガウス?)を推定する。 ? ベイズモデル比較 事前分布:? ?? 尤度関数(3.68):? ? ?? = ??? ? ? ?, ?? ? ? ?? ?? 事後分布(3.66): p ??|? ∝ ? ?? ? ? ?? ? 事前分布は各々のモデルに対する好みを表す(好きなモデルに高い 確率を???)。ここでは事前確率は等しいと考える。 ? 尤度関数をモデルエビデンスと呼び、データから見たモデルの好み を表す。 3.4 ベイズモデル比較
- 16. - 16 - ? 予測分布 予測分布(3.67):? ? ?, ? = σ?=1 ? ? ? ?, ??, ? ?(??|?) ? 混合分布の一種(全てのモデルの総和を取るので、各モデルの予測 値を元に一つの t を算出する)。 ? モデルエビデンス( ? ? ?? ) ? あるモデル?? から教師データD が生成される確率。 ? ベイズの定理でパラメータwの事後確率を計算するときの分母に モデルエビデンスが出現する。 ? モデルエビデンスはwを周辺化した尤度関数(周辺尤度) wの事後分布(3.69): ? ? ?, ?? = ?(?|?,? ?)?(?|? ?) ?(?|? ?) ? ある二つのモデルエビデンスの比はベイズ因子と呼ばれる。 ベイズ因子: ?(?|??) ?(?|? ?) 3.4 ベイズモデル比較
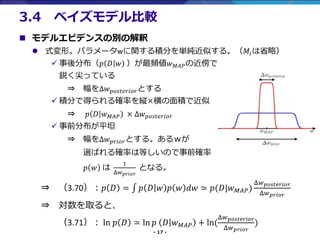
- 17. - 17 - ? モデルエビデンスの別の解釈 ? 式変形。パラメータwに関する積分を単純近似する。(??は省略) ? 事後分布(? ? ? )が最頻値? ???の近傍で 鋭く尖っている ? 幅をΔ? ?????????とする ? 積分で得られる確率を縦×横の面積で近似 ? ? ? ? ??? × Δ? ????????? ? 事前分布が平坦 ? 幅をΔ? ?????とする。あるwが 選ばれる確率は等しいので事前確率 ? ? は 1 Δ? ????? となる。 ? (3.70):? ? = ??? ? ? ? ? ? ?? ? ?(?|? ???) Δ? ????????? Δ? ????? ? 対数を取ると、 (3.71): ln ? ? ? ln ? ? ? ??? + ln( Δ? ????????? Δ? ????? ) 3.4 ベイズモデル比較
- 18. - 18 - ? モデルエビデンスの別の解釈(続き) (3.71): ln ? ? ? ln ? ? ? ??? + ln( Δ? ????????? Δ? ????? ) ? Δ? ????????? < Δ? ????? なので、ペナルティ項は常に負。 Δ? ????? に対して Δ? ????????? が小さい(幅が狭く)なると ペナルティが強くなる(負の値が大きくなる)。 ? 幅がせまい=過学習(モデルが複雑)の可能性がある。 ? モデルがM個のパラメータを含む場合 (3.72): ln ? ? ? ln ? ? ? ??? + ? ln( Δ? ????????? Δ? ????? ) ? パラメータが多いとペナルティ大。 ? バランスの良いモデルが選択される。 3.4 ベイズモデル比較 データへのフィッティング度 ペナルティ項 AIC:あるモデルを選択した時に、説明変数の数にペナルティ BIC:あるモデルを選択した時に、訓練データ数にペナルティ モデルエビデンス:いくつかのモデルがあった時に、そのモデルの複雑さにペナルティ
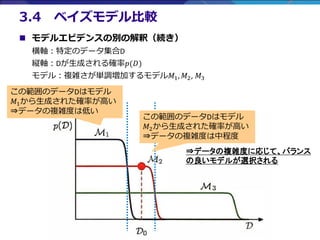
- 19. - 19 - ? モデルエビデンスの別の解釈(続き) 横軸:特定のデータ集合D 縦軸:Dが生成される確率?(?) モデル:複雑さが単調増加するモデル?1, ?2, ?3 3.4 ベイズモデル比較 この範囲のデータDはモデル ?1から生成された確率が高い ?データの複雑度は低い この範囲のデータDはモデル ?2から生成された確率が高い ?データの複雑度は中程度 ?データの複雑度に応じて、バランス の良いモデルが選択される
- 20. - 20 - ? 正しいモデルを選択 ? ベイズモデル比較では、考えているモデル集合の中にデータが生成される 真の分布が含まれていることを暗に仮定。 ? この仮定が正しければ、ベイズモデル比較によって平均的に 正しいモデルが選択される。(正しいモデルが選択される確率高) ? 2つのモデル(?1, ?2)のうち、?1が正しいモデルだと仮定する。 ? ベイズ因子の期待値を計算。 期待ベイズ因子 (3.73):??? ? ? ?1 ln ?(?|?1) ?(?|?2) ?? (?1が選択された時のデータDが生成される確率× ?1に関するベイズ因子 における全データの積分値) ? この式はKLダイバージェンスと同じ KLダイバージェンス:??(?| ? ? ??? ? ? ln ?(?) ?(?) ?? ? KLダイバージェンスは常に正。 つまり、常に?(?|?1)> ?(?|?2)であることが期待できる。 3.4 ベイズモデル比較 ※KL???????????:Kullback–Leibler divergence


![- 3 -
3.3 ベイズ線形回帰
? 今までの内容で分かったこと(最尤推定の場合)
? 基底関数の数によって決まるモデルの複雑さをデータサイズに応じて
決定する必要性
? 正則化項(Lasso, Ridge etc)を追加することによって、モデルの複雑さ
を調整可能(基底関数の数と形を選ぶことは正則化を付けても重要)
? 解こうとしている問題に合わせてモデルの複雑さを決める必要
? 尤度最大化では、常に複雑なモデルを選択する危険性(過学習)
? 過学習への対処
? クロスバリデーション
学習、評価、テストの3つに分割するのが一般的。以下手順。
①[学習, 評価]の組み合わせをkに分割し、
k-1個のデータで学習、1個で評価。入れ替えながらハイパラ探索。
②ベスパラで[学習, 評価]データ全てを学習し、1つのモデルを作成。
③テストデータで性能評価。
? これを複数モデルで実施して、テストデータでの評価結果を比較
(計算量が多い)。手元にある一部のデータを学習に使えない。](https://image.slidesharecdn.com/prml33-191218152147/85/PRML-3-_3-3-3-4-3-320.jpg)