![参考書籍
? Farrell, S., & Lewandowsky, S.
(2018). Computational
Modeling of Cognition and
Behavior. Cambridge
University Press. [LINK]
? Robert, C. (2017). Statistical
Rethinking. CRC Press.
[LINK]
? Watanabe, S.
(2018). Mathematical theory of
Bayesian statistics. CRC
Press. [LINK]
61](https://image.slidesharecdn.com/bayesjuku0630b-180630144427/85/-61-320.jpg)
これからの仮説検証?モデル评価
- 2. はじめに 名前：北條大樹 所属：東京大学 教育学研究科 教育心理学コース D1 研究室：心理統計学研究室（指導教員：岡田 謙介） 研究関心：ベイズ統計学?心理統計学?数理心理学 HP : https://dastatis.github.io/index.html OSF : osf.io/7d9zw Github : https://github.com/dastatis Twitter : @dastatis 2
- 3. 本日の流れ ?心理学者におけるベイズ統計について ? 事後分布が出てくるまで ? 事前分布について ? どうやってデータ生成メカニズムを考えるのか？ ?事後分布の取り扱い方 ? 事後分布の点要約 ? 事後分布の区間要約 ?これからの仮説検証?モデル评価 ? 我々はどちらに興味があるのか？ ? 周辺尤度＋α ? 事後予測チェックについて ? 情報量規準について 3
- 5. Big Picture for Bayesian inference 5 Watanabe (2018) P.4 Figure1.1より引用 (公式： https://www.taylorfrancis.com/books/9781482238082 )
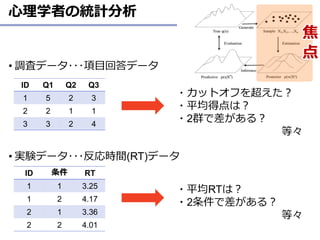
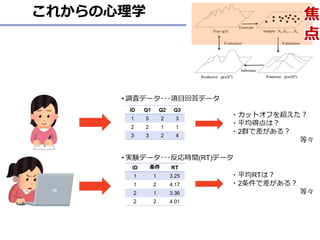
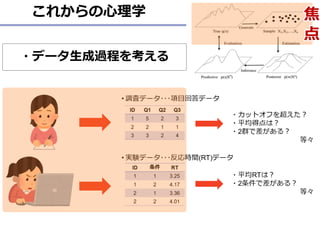
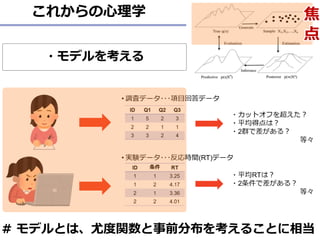
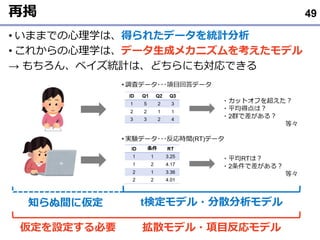
- 6. 心理学者の統計分析 ? 調査データ???項目回答データ ? 実験データ???反応時間(RT)データ 6 ID 条件 RT 1 1 3.25 1 2 4.17 2 1 3.36 2 2 4.01 ID Q1 Q2 Q3 1 5 2 3 2 2 1 1 3 3 2 4 ?カットオフを超えた？ ?平均得点は？ ?2群で差がある？ 等々 ?平均RTは？ ?2条件で差がある？ 等々 焦 点
- 7. これからの心理学 焦 点
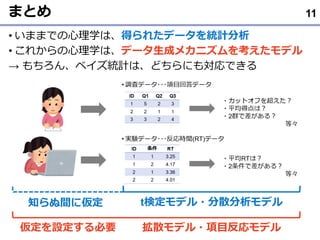
- 11. まとめ ? いままでの心理学は、得られたデータを統計分析 ? これからの心理学は、データ生成メカニズムを考えたモデル → もちろん、ベイズ統計は、どちらにも対応できる 11 t検定モデル?分散分析モデル 拡散モデル?項目反応モデル 知らぬ間に仮定 仮定を設定する必要
- 12. 事後分布がでてくるまで ? パラメータ推定の文脈で?我々の興味のあるパラメータθの不 確かさを観測データyから求めるとき ? ? ? = ? ? ? ?(?) ?(?) と表す ? しかし、実際はMCMC等で事後分布を導出するので ? ? ? ∝ ? ? ? ?(?) 必要なのは、尤度と事前分布のみ 12 事前分布尤度事後分布 周辺尤度 事前分布尤度事後分布 * ∝…は比例を表す Next 事前分布をどうやって選ぶ? ?
- 13. 事前分布選びかたの一例 ? 得られたデータの生成メカニズムを考えるならば、○○という仮定を置 くことにしよう ? 論文ではこれを客観的に説明する。 ex) 成人男性の身長の事前分布 × 0－∞(限りなく広い正)の範囲の一様分布 ○ 1.65m(成人男性の平均身長)を平均とする正規分布 ? データ生成メカニズムを考えたモデルのパラメータ推定がうまくいかな いため、推定可能となるような事前分布を設定する ? 論文では、モデルの仮定の一つとして上記の事前分布を置いたことを 説明し、モデルの挙動を正確に記述する。また、分析を再現可能な形と して論文とともに提出し、査読を受ける。論文化される場合、分析コー ドを公開する。現段階でモデルの最善を尽くした結果、このような仮定 （事前分布）のモデルになった ? これによって、別の研究者がそのコードに基づいて再現、改良を加え ることができる、もしくは、計算技術の向上等で、より自然な仮定のモ デルが誕生。当該領域の研究の発展につながる 13 ＃ 研究目的に応じて、適切に使い分けるべき
- 14. まとめ ? 事後分布を導出するためには、尤度と事前分布が必要 ? 事前分布の設定をどうすべきか？ ? あなたの研究目的は？何が知りたい？ ? 事後分布を導出するためには(再掲) ? ? ? ∝ ? ? ? ?(?) Next データ生成(尤度の部分)をどうやって考えていく? ? 得られたデータを統計分析 ? 既にモデルが定まっていることが多い ? データ生成メカニズムを考えたモデル ? 既存のモデルをベースを元に自分組み立てて行く 14 事前分布尤度事後分布
- 16. モデリングで大事なことをあげるなら ? データ生成メカニズムを考えたモデルのために何を？ ? データをあらゆる視点から眺める ? 眺めるとは、単純な可視化?記述統計?相関を算出すること データがどのような形状(分布)なのか？(属性別?個人別にも出してみる) ? データがどのような環境?背景?人物?時間で取れたのか ? 他に使えそうなデータを捨ててしまった or 取りこぼしていないか？ 実験デザイン?調査デザイン全体を通したデータが得られるまでの過程 を隅々まで追求する 16 ヒストグラム?散布図を描く 本来、統計分析は事前にやることがたくさん これからの仮説検証?モデル评価には これらが非常に重要になってくる *ベイズか否かは、ここではあまり関係ない
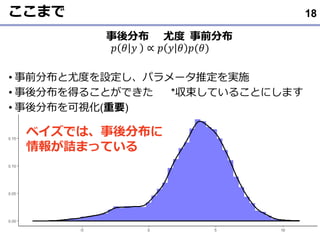
- 18. ここまで ? ? ? ∝ ? ? ? ?(?) ? 事前分布と尤度を設定し、パラメータ推定を実施 ? 事後分布を得ることができた *収束していることにします ? 事後分布を可視化(重要) 18 事前分布尤度事後分布 ベイズでは、事後分布に 情報が詰まっている
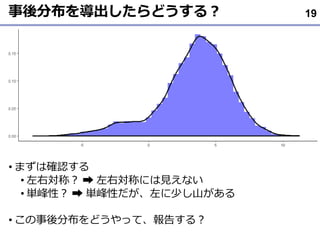
- 19. 事後分布を導出したらどうする？ ? まずは確認する ? 左右対称？ ? 左右対称には見えない ? 単峰性？ ? 単峰性だが、左に少し山がある ? この事後分布をどうやって、報告する？ 19
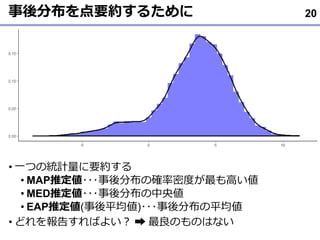
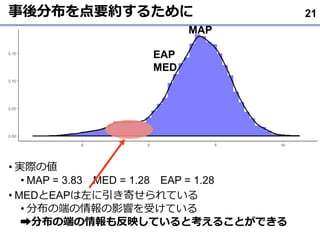
- 20. 事後分布を点要約するために ? 一つの統計量に要約する ? MAP推定値???事後分布の確率密度が最も高い値 ? MED推定値???事後分布の中央値 ? EAP推定値(事後平均値)???事後分布の平均値 ? どれを報告すればよい？ ? 最良のものはない 20
- 21. 事後分布を点要約するために ? 実際の値 ? MAP = 3.83 MED = 1.28 EAP = 1.28 ? MEDとEAPは左に引き寄せられている ? 分布の端の情報の影響を受けている ?分布の端の情報も反映していると考えることができる 21 MAP EAP MED
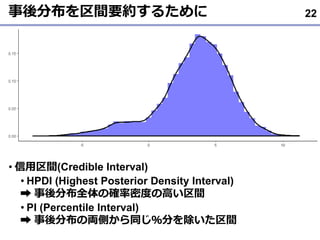
- 22. 事後分布を区間要約するために ? 信用区間(Credible Interval) ? HPDI (Highest Posterior Density Interval) ? 事後分布全体の確率密度の高い区間 ? PI (Percentile Interval) ? 事後分布の両側から同じ％分を除いた区間 22
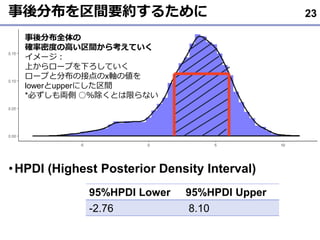
- 23. 事後分布を区間要約するために ?HPDI (Highest Posterior Density Interval) 23 事後分布全体の 確率密度の高い区間から考えていく イメージ： 上からロープを下ろしていく ロープと分布の接点のx軸の値を lowerとupperにした区間 *必ずしも両側 ○％除くとは限らない 95%HPDI Lower 95%HPDI Upper -2.76 8.10
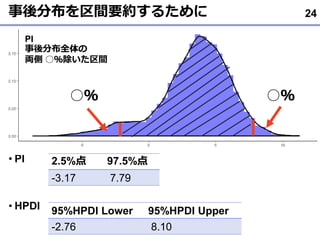
- 24. 事後分布を区間要約するために ? PI ? HPDI 24 PI 事後分布全体の 両側 ○％除いた区間 2.5%点 97.5%点 -3.17 7.79 95%HPDI Lower 95%HPDI Upper -2.76 8.10 ○％ ○％
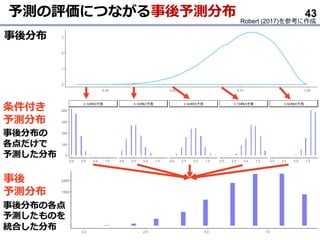
- 25. まとめ ? 事後分布を点?区間要約するには？ ? 点であれば、MAP/MED/EAP推定値というまとめ方がある ? MED/EAPは、分布が左右非対称の場合、分布の端の情報を 反映させることができる ? 報告の際に、余裕があるのであれば全て報告した方が良い？ ? 大体一致しているならば、その旨を書いても良いかも ? 区間であれば、同じ信用区間という呼び名でも2種類 （ HPDIとPI ）ある ? 報告の際は、どちらの信用区間なのか記述すべき ? もし、二つの区間幅の違いが大きいようであれば、そもそも 区間要約は適切ではないかもしれない(Robert, 2017) 25 要約は便利でわかりやすいが、 事後分布の大事な情報を削りすぎないよう注意が必要 可能な限り事後分布を報告 (付録や補足資料としてOSF等にUP)
- 30. ベイジアンは事後分布で終了ではない 30 Watanabe (2018) P.4 Figure1.1より引用 (公式： https://www.taylorfrancis.com/books/9781482238082 )
- 31. ベイジアンは予測評価までで一連の枠組み 31 Watanabe (2018) P.4 Figure1.1のみ引用 (公式： https://www.taylorfrancis.com/books/9781482238082 )
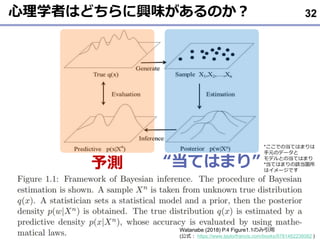
- 32. 心理学者はどちらに興味があるのか？ 32 Watanabe (2018) P.4 Figure1.1のみ引用 (公式： https://www.taylorfrancis.com/books/9781482238082 ) 予測 “当てはまり” *ここでの当てはまりは 手元のデータと モデルとの当てはまり *当てはまりの該当箇所 はイメージです
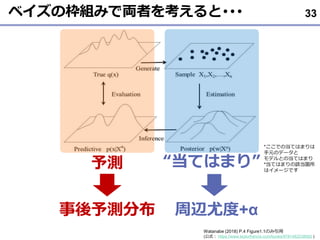
- 33. ベイズの枠組みで両者を考えると??? 33 Watanabe (2018) P.4 Figure1.1のみ引用 (公式： https://www.taylorfrancis.com/books/9781482238082 ) 予測 “当てはまり” 事後予測分布 周辺尤度+α *ここでの当てはまりは 手元のデータと モデルとの当てはまり *当てはまりの該当箇所 はイメージです
- 34. 当てはまり評価につながる周辺尤度+α ? 周辺尤度って何？ ? ? ? = ? ? ? ?(?) ?(?) = ? ? ? ? ? ∫ ? ? ? ?(?)?? ? ベイズの定理の分母の部分 ? MCMC等での事後分布の導出には、尤度と事前分布があればよかった ので使ってなかった ? 現在のデータとモデルの当てはまりを表す周辺尤度+αとは？ 自由エネルギーのこと ? 周辺尤度から計算できる *自由エネルギーって何？ ?これは、いろいろ端折ると真の分布と確率モデルの近さを表す ? 複数のモデルにおける自由エネルギーを比較することで 現在のデータとモデルの当てはまりを評価できる ? 心理学現象の解釈につながる 34 事前分布尤度 事後分布 周辺尤度 事前分布尤度 周辺尤度 ここら辺の 詳しい話は 清水先生の資料へ
- 35. 自由エネルギーを算出した ? 3つのモデルの自由エネルギーをそれぞれ算出した ? 自由エネルギーは相対指標なので、いくつ以下になるとOKみ たいなものはない！ ? 上に示しているのは例であり、これより大きくなることも小さくなるこ とも当然ある ? 論文にするならば、以下のように解釈できる ? ３つのモデルの自由エネルギーを比較するとモデル３が最も 低いので、ほかの２つよりも、現在のデータから得られたモ デルと真のモデルが近いと解釈できる 35 モデル1 モデル2 モデル3 自由エネルギー -500 -600 -10000
- 36. もっと、良いモデルがあるかもしれない？？ ? 今回は３つのモデルを比較した ? 検討していない第４のモデルの自由エネルギーを算出したら -100000000かもしれない ? モデルは常に間違っていると前提しておく ? 今のモデルが正しいことをチェックするのではなく，観測 データをどれだけ記述できていないかを考える(Robert, 2017) ? Next 周辺尤度とベイズファクターについて ? ? 二つのモデルを比較するならば… 36 モデル1 モデル2 モデル3 自由エネルギー -500 -600 -10000
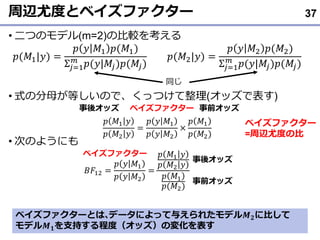
- 37. 周辺尤度とベイズファクター ? 二つのモデル(m=2)の比較を考える ? 式の分母が等しいので、くっつけて整理(オッズで表す) ? 次のようにも 37 ?(?1|?) = ? ? ?1 ?(?1) Σ?=1 ? ?(?|??)?(??) ?(?2|?) = ? ? ?2 ?(?2) Σ?=1 ? ?(?|??)?(??) 同じ ? ?1 ? ? ?2 ? = ? ? ?1 ? ? ?2 × ? ?1 ?(?2) 事後オッズ 事前オッズベイズファクター ??12 = ? ? ?1 ? ? ?2 = ? ?1 ? ? ?2 ? ? ?1 ?(?2) ベイズファクター 事後オッズ 事前オッズ ベイズファクターとは?データによって与えられたモデル? ?に比して モデル? ?を支持する程度（オッズ）の変化を表す ベイズファクター =周辺尤度の比
- 38. ベイズファクターを求める ? モデル(仮説)１とモデル(仮説) ２を用意して、比較を行った ? すると??12 = 3と求まった。これはどういう意味だ ? 現在得られたデータはモデル2より、モデル１のほうが3倍 上手に表現できる（あってる？） ? このように、2つのモデル比較を事前オッズと事後オッズ比で 考えることができる ? Nullモデルを用意して、検定っぽく比較することもあります ? これに関連して、詳細を知りたい人はSavage-Dickey法な どと併せて、検索してみてください(怖い人本等)へ ? ただ、ベイズファクターは比なので、片方のモデルがおかし いと、とても大きな影響を受ける ?事前分布等の影響を大きく受ける(後述) 38
- 39. 実際の手順 ? 周辺尤度を算出する ? 自由エネルギー or ベイズファクターをもとめる ? じゃあ、なんでこんなに便利なのに今まで使われなかったの か？ ? 周辺尤度を算出するのが大変だった（心理学者は特に） ? 心理学で事前分布に関する議論が（あまり）行われなかった 39
- 40. これまでの周辺尤度事情 ? 周辺尤度を計算できないケースが多かった どんなケースで計算が難しかったのか? ? 非線形モデル ? パラメータ数が多い場合(特に階層モデル) ? しかし、近年、周辺尤度を計算できない時代は終わりを告げ ようとしている 1. Naive Monte Carlo Estimator 2. Importance Sampling Estimator 3. Generalized Harmonic Mean Estimator 4. Bridge Sampling 5. WARP-III bridge sampling or WARP-U bridge sampling 40 詳しい話は、ここ
- 41. 周辺尤度の弱点をどうするか ? 周辺尤度は事前分布の影響を大きく受ける ? 事前分布の選択がとても重要になる ? 清水(2018)は、心理学者も真剣に事前分布を考える時だ と提言 ? Farrell & Lewandowsky (2018)では、心理学者がベイズ ファクター使用する際の事前分布をどうすべきか解説 ?曖昧な事前分布はかえって、ベイズファクターに悪影響 ?ベイズファクターがすべてのモデル比較を解決するわ けではない ?ベイズファクターの基準を決めて判断するのはナンセン ス 41
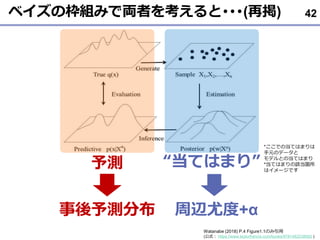
- 42. ベイズの枠組みで両者を考えると???(再掲) 42 Watanabe (2018) P.4 Figure1.1のみ引用 (公式： https://www.taylorfrancis.com/books/9781482238082 ) 予測 “当てはまり” 事後予測分布 周辺尤度+α *ここでの当てはまりは 手元のデータと モデルとの当てはまり *当てはまりの該当箇所 はイメージです
- 44. 事後予測分布の扱い方 ? 事後予測分布と実際のデータの分布を比較してみる ? 大きな相違がなければ、今回のベイズモデルの予測がきちん とできていることを表す Next 事後予測分布以外の予測について検討する方法 情報量規準の話? 44
- 45. 情報量規準(AIC?DIC?WAIC / LOO ) ? WAICやLOOという情報量規準によって、将来予測の観点から モデルを評価することができる。 ? WAICって何？ ? とても省略して書くと、AICの改良の改良版 ? AICは、複雑すぎるモデルが”良い”モデルとされないために罰則を付加 ?しかし、この計算には最尤推定値が用いられている ? ベイズでいうと、MAP推定値が用いられていることを指す ? ここで、事後分布の点要約の話を思い出そう ? MAP推定値は事後確率密度の高いところ表現する代わりに、ゆがんだ 分布だと分布の端の情報を考慮できない ?では、計算に事後平均値(EAP)を使ってやろう！ってのがDIC しかし、ベイズの本質を改めて思い出してほしい ベイズでは、事後分布に全ての情報が込められている ?事後分布の各点の値を用いて、計算を行おう！ってのがWAIC 45 *注：DICもWAICも 罰則項も変化している
- 46. 情報量規準つづき ? LOOって何？(LOOは、PSIS-LOO,LOO-CVとも呼ばれる) ? 正式名称は ? やっていることは、PSISというすごいアルゴリズムに基づ いて、データを1つとって、それを残りのデータで予測でき るかをすべての組み合わせで繰り返す ? WAICとLOOは近い値になる。そういう性質がある 46 Pareto Smooth Importance Sampling – Leave One Out – Cross Validation
- 47. まとめ ? 予測に興味がある？当てはまりに興味がある？ ? 当てはまりなら、周辺尤度を考えることが非常に重要になっ てくる ? 自由エネルギーやベイズファクターとお友達になろう ? 適切な事前分布の選択が必要になる ? 予測なら、事後予測分布を書いてみるのが大事 ? また、別の方法として情報量規準による方法もある ? 基本的にこれらの指標は相対的な指標である ? どんなモデルチェックやモデル比較にも有効な手段は存在し ない。状況に応じて方法を変える必要あり ? そのために引き出しを増やそう 47 モデル比較で決めるよりも試行錯誤を繰り返して “素晴らしい”モデルを作ろう
- 49. 再掲 ? いままでの心理学は、得られたデータを統計分析 ? これからの心理学は、データ生成メカニズムを考えたモデル → もちろん、ベイズ統計は、どちらにも対応できる 49 t検定モデル?分散分析モデル 拡散モデル?項目反応モデル 知らぬ間に仮定 仮定を設定する必要
- 50. どっちから始める？ ? いままでの心理学は、得られたデータを統計分析 ? こちらから始めるのが楽 ? これからの心理学は、データ生成メカニズムを考えたモデル ? ベイズの雰囲気がわかってきたらこっち/別に初めからでも ? どう始める？ ? 得られたデータを統計分析 ? JASP ? 最後にこのお話と実践 ? データ生成メカニズムを考えたモデル ? brms / JAGS / Stan ? こちらを学びたい人は、関連書籍や午後の話を参考にしてね 50
- 51. 51
- 52. JASPとは？ ? JASPは、統計解析を行うための新たな”方法”(ソフト)である。 ? 完全無料 ? オープンソース ? クロスプラットフォーム ? 見やすい画面、そして、ドラッグ&ドロップ操作で簡単に統計 分析できる ? JASPは、ANOVAや回帰分析のような古典的分析だけでなく、 それらのベイズ統計分析も実施することができる ?モデリングはできない ? まだ誕生したばかり?開発が盛ん(すぎて資料作りに困った) https://jasp-stats.org/releases/DISCOVER_JASP_2017.pdf より 52
- 53. なぜJASPを使うのか？ ? 多くの利点 ? SPSSのような商用パッケージと比較して、JASPは無料で、オープン ソースで、開発が盛ん、そして、パラメータ推定法としてベイズ法を使 える。 ? Rのようなフリーパッケージと比較しても、ドラッグ&ドロップで簡単 に操作できる。プログラミング能力を必要としない。 ? その他の全てのパッケージと比べて、JASPは基本となる分析を古典的 かつベイズ的に実行することができる。 ? Windows/Mac/Linux の全てで使用することが可能である。 https://jasp-stats.org/releases/DISCOVER_JASP_2017.pdf より 53
- 54. JASPの詳細 ? JASPって何の略？ ? Jeffereys’s Amazing Statistics Program ? Bayesian pioneer Sir Harold Jeffreysが驚愕の統計プログラム ? JASPって何のプログラミング言語で書かれているの？ ? アプリケーション自体はC++で書かれている。 ? 分析は、RとC++のどちらもで書かれている(R packageも導入済)。 ? その他、ソフト外観でjavascriptも使用されている。 ? どのライセンスでJASPは公開されているのか？ ? The GNU Affero General Public License, Version 3 54 https://jasp-stats.org/faq/ より
- 56. JASP起動時 56
- 57. 分析時の画面 57
- 58. 実際に操作をお見せします 58
- 60. もっともっと使えるようになりたい？ ? 日本心理学会 第82回大会＠仙台にて ワークショップ 「心理学者のためのJASP統計解析入門」 開催します(通ってればｗ) 興味があればご検討ください 60
- 61. 参考書籍 ? Farrell, S., & Lewandowsky, S. (2018). Computational Modeling of Cognition and Behavior. Cambridge University Press. [LINK] ? Robert, C. (2017). Statistical Rethinking. CRC Press. [LINK] ? Watanabe, S. (2018). Mathematical theory of Bayesian statistics. CRC Press. [LINK] 61