More Related Content What's hot (20)
SSII2021 [OS2-01] 転移学習の基礎:異なるタスクの知識を利用するための機械学習の方法 SSII2021 [OS2-01] 転移学習の基礎:異なるタスクの知識を利用するための機械学習の方法
SSII ?
SSII2021 [OS2-01] 転移学習の基礎:異なるタスクの知識を利用するための機械学習の方法
6月10日 (木) 11:00 - 12:30 メイン会場(vimeo + sli.do)
登壇者:松井 孝太 氏(名古屋大学)
概要:転移学習とは、解きたいタスクに対して、それと異なるが似ている他のタスクからの知識(データ、特徴、モデルなど)を利用するための方法を与える機械学習のフレームワークです。深層モデルの学習方法として広く普及している事前学習モデルの利用は、この広義の転移学習の一つの実現形態とみなせます。本発表では、まず何をいつ転移するのか (what/when to transfer) といった転移学習の基本概念と定式化を説明し、具体的な転移学習の主要なアプローチとしてドメイン適応、メタ学習について解説します。
Similar to 演習発表 Sari v.1.1 (20)
NLP2012 NLP2012
Yuki Nakayama ?
試しにアップロード。
NLP2012で発表(pdf版)。
修士論文執筆の傍らでやってた趣味的研究。
あわよくば,発展させて論文化できたらいいな( ??`)
More from Lutfiana Ariestien (6) 1. [論文紹介]
A Subsequence Matching with Gaps-Range-
Tolerances Framework:
A Query-By-Humming Application
システム情報科学府?情報学専攻
修士1年?池田研究室
ルトフィアナ?サリ?アリスティン
2012 年 12 月 18 日 (火)
情報演習発表
1
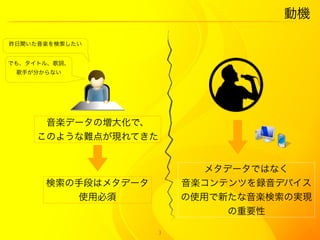
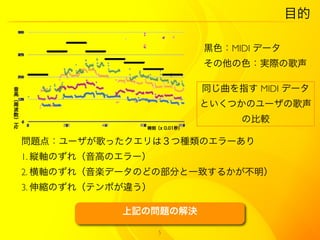
5. 目的
黒色:MIDI データ
その他の色:実際の歌声
同じ曲を指す MIDI データ
といくつかのユーザの歌声
の比較
問題点:ユーザが歌ったクエリは3つ種類のエラーあり
1. 縦軸のずれ(音高のエラー)
2. 横軸のずれ(音楽データのどの部分と一致するかが不明)
3. 伸縮のずれ(テンポが違う)
上記の問題の解決
5
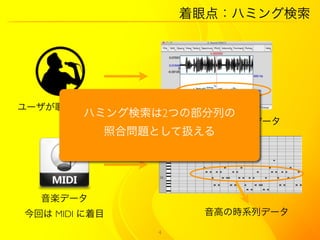
6. 論文紹介
[タイトル]
A Subsequence Matching with Gaps-Range-Tolerances
Framework: A Query-By-Humming Application
[著者]
Alexios Kotsifakos, Panagiotis Papapetrou, Jaakko Hollmén,
Dimitrios Gunopulos
[書誌情報]
Proceeding of the VLDB Endowment, Vol. 4, No. 11 2011
[概要]
データ処理の観点からハミング検索の問題を解決する.ユーザが
歌ったクエリと音楽データを完全一致させるのではなく、許容範
囲内を設定することで一致条件をあげる.
6
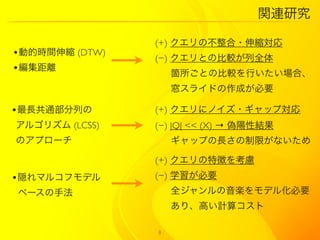
8. 関连研究
(+) クエリの不整合?伸縮対応
?動的時間伸縮 (DTW) (?) クエリとの比較が列全体
?編集距離 箇所ごとの比較を行いたい場合、
窓スライドの作成が必要
?最長共通部分列の (+) クエリにノイズ?ギャップ対応
アルゴリズム (LCSS) (?) |Q| << (X) → 偽陽性結果
のアプローチ ギャップの長さの制限がないため
(+) クエリの特徴を考慮
?隠れマルコフモデル (?) 学習が必要
ベースの手法 全ジャンルの音楽をモデル化必要
あり、高い計算コスト
8
11. 問題定式化のための定義
音楽データ: X = {x1 , ..., xn }
クエリは音楽データと同様
音楽データの長さ :|X|
p Q = {q1 , ..., qm }
xj =< x j , xr
j >∈ X p r
|Q|, qi =< qi , qi >∈ X
DB = {X1 , ..., XN }
Q[ts : te] = {qts , ..., qte }
X[ts : te] = {xts , ..., xte }
定義 1
p
qi ≈f xj とは = {f , f } という許容の条件下で
p r f (i) = fp (qi )
p
qi ∈ Q と xj ∈ X が一致するとする f (i, j) = fr (qi , xr )
p
r
j
定義 2
同じ長さの Q[ts1 : te1 ] と X[ts2 : te2 ] に対し、 i ≈f xj
q ?πi ∈ GQ
SM BGT (Q, X) ? te2 ? ts2 ≤ r は下記を満たす: ?γj ∈ GX
f
qi ≈ xj ∧ πi+1 ? πi ? 1 ≤ β, γj+1 ? γj ? 1 ≤ α i = 1, ..., |GQ |
11
12. 问题定式化のための定义(例)
Q = {6, 3, 10, 5, 3, 2, 9}, X = {1, 1, 3, 4, 6, 9, 2, 3, 1}
Q[2 : 6] ∧ GQ = {2, 4, 5, 6} ? {3, 5, 3, 2}
X[3 : 8] ∧ GX = {3, 4, 7, 8} ? {3, 4, 2, 3}
次のパラメータを設定する: = 1, α = 2, β = 1, r = 6
{3, 5, 3, 2} vs {3, 4, 2, 3}
α = 2 → {3, , , 2}
{Q[2 : 6], X[3 : 8]} は SM BGT (Q, X)
β = 1 → {3, , 2, }
問題の定式
|SM BGT (Q, Xi [ts : te])| ≥ δ の条件下で
トップ K の S = {Xi [ts : te]|Xi ∈ DB} 見つける
δ は正の整数
12
13. 提案手法:SMBGT
input : Q, X, α, β, f
, r, パラメータ K
入力と出力
output: プライオリティキュー S
begin
S=null
for t ← 1 to |DB| do
bestvalue = 0
行列 |Xj | × |Q| として動的に比較される
beststart = 0
for j ← 1 to |Xt | do
for i ← 1 to |Q| do
if qi ≈f xj then 一致しない場合、伝搬という意味の関
curi .value = previ?1 .value + 1
curi .start = previ .start 数を動かす
end ターゲットからの伝搬: j ? Aprev (i) ≤ α
start
else prev
クエリからの伝搬:i ? Bstart (i ? 1) ≤ β
curi = propagation(i, j, Astart , Bstart )
end
end 1つ SMBGT を見つけた後、r の条件
best = U pdate(j, cur)
を違反しないかチェック
cur = ResetB (j, cur, Astart , Bstart )
end
qi = xj の場合、行列 |Xj | × |Q| をリセット
U pdatequeue (S, best, K)
end
end 13
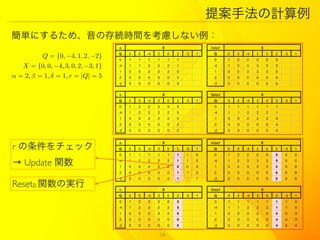
14. 提案手法の計算例
簡単にするため、音の存続時間を考慮しない例:
a X Astart X
Q 0 0 -4 3 0 2 -3 1 Q 0 0 -4 3 0 2 -3 1
Q = {0, ?4, 1, 2, ?2} 0 1 1 1 1 1 1 0 1 2 2 2 5 5
X = {0, 0, ?4, 3, 0, 2, ?3, 1} -4 1 1 2 2 2 1 -4 1 2 3 3 3 5
1 0 0 2 2 2 0 1 0 0 3 3 3 0
α = 2, β = 1, δ = 1, r = |Q| = 5 2 0 0 0 0 0 3 2 0 0 0 0 0 6
-2 0 0 0 0 0 3 -2 0 0 0 0 0 6
s X Bstart X
Q 0 0 -4 3 0 2 -3 1 Q 0 0 -4 3 0 2 -3 1
0 1 2 2 2 5 5 0 1 1 1 1 1 1
-4 1 2 2 2 2 5 -4 1 1 2 2 2 1
1 0 0 2 2 2 0 1 0 0 2 2 2 0
2 0 0 0 0 0 2 2 0 0 0 0 0 4
-2 0 0 0 0 0 2 -2 0 0 0 0 0 4
a X Astart X
r の条件をチェック Q 0 0 -4 3 0 2 -3 1 Q 0 0 -4 3 0 2 -3 1
0 1 1 1 1 1 1 1 0 0 1 2 2 2 5 5 5 0
→ Update 関数 -4
1
1
0
1
0
2
2
2
2
2
2
1
0
1
0
0
2
-4
1
1
0
2
0
3
3
3
3
3
3
5
0
5
0
0
8
2 0 0 0 0 0 1 1 2 2 0 0 0 0 0 6 6 8
-2 0 0 0 0 0 1 1 1 -2 0 0 0 0 0 6 6 6
ResetB 関数の実行 s X Bstart X
Q 0 0 -4 3 0 2 -3 1 Q 0 0 -4 3 0 2 -3 1
0 1 2 2 2 5 5 0 1 1 1 1 1 1 1 0
-4 1 2 2 2 2 5 -4 1 1 2 2 2 1 1 0
1 0 0 2 2 2 0 1 0 0 2 2 2 0 0 3
2 0 0 0 0 0 6 2 0 0 0 0 0 4 4 3
-2 0 0 0 0 0 6 -2 0 0 0 0 0 4 4 4
14
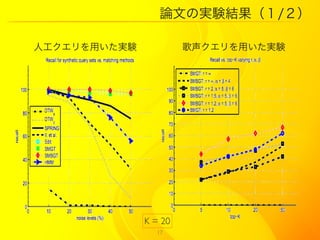
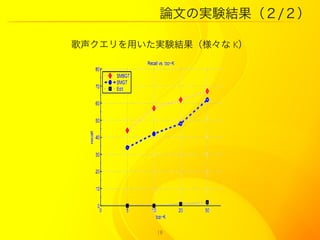
15. 論文の実験
音楽データ:5643 MIDI ファイル(様々なジャンル)
人工クエリ:音楽データの一部をとったもの 6 セット
(1セット = 100 個)、任意の長さ
歌声のクエリ:100個の歌声、任意の長さ
Q0 , Q.10 , Q.20 , Q.30 , Q.40 , Q.50
Qx ? x × noise
|Q|min = 13, |Q|max = 137
|Qhum |min = 14, |Qhum |max = 76
手法?:SMBGT (Subsequence Matching with Bounded Gaps and
Tolerances
15
16. 音高の表现
周波数 (frequency) は音高を表すが
人間が聞いた2倍高い音高 ≠ 周波数が2倍
人間が聞いた2倍高い音高 = 周波数の対数が2倍
MIDI データにおいて、音高?→?semitone
f requency
semitone = 12 × log2 + 69
440
人間が聞いた2倍の音高 = 2倍の semitone
実験では音高を semitone に変換
16
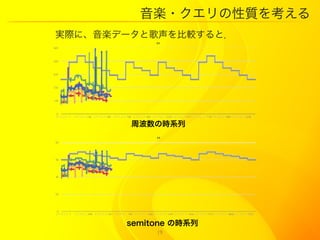
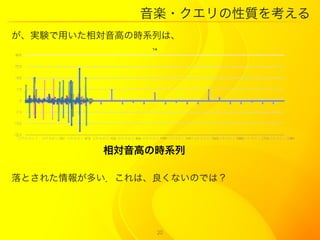
21. 音楽?クエリの性質を考える
平均値との差 元々の時系列の要素をその
列の平均値や中央値と差を
とり、一致させたもの
グレイ:対応する音楽
データの列
中央値との差 その他:対応する音楽
データと同じも
のを歌ったいく
つかの歌声
21
23. 発表者の実験
評価方法
再現率:何%のクエリの正解結果がトップ K 個に入ったか
MRR (Mean Reciprocal Rank):ランクの平均逆数
N
1
1
M RR =
N n=1 rankn
様々な前処理で行った結果
1.000
0.875
0.750
0.625
0.500
0.375
0.250
0.125
0
最低音との差 [ED] 最低音との差 [DTW] Vocaloid [ED] Vocaloid [DTW] 平均値との差 [ED] 平均値との差 [DTW] 中央値との差 [ED] 中央値との差 [DTW]
MRR K=10 の再現率
平均値との差で、編集距離も DTW も K=10 で 0.9098 の再現率
→前処理が重要なのではないか
23
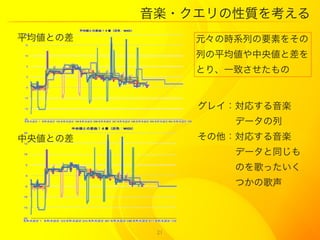
24. 発表者の実験
同じ音楽データの部分の歌声はどの程度違うか?
クエリのデータセット→ 50% ターゲットとし、50% 検索クエリとした
様々な前処理で行った歌声-歌声の結果
1.000
0.875
0.750
0.625
0.500
0.375
0.250
0.125
0
最低音との差 [ED] 最低音との差 [DTW] 平均値との差 [ED] 平均値との差 [DTW] 中央値との差 [ED] 中央値との差 [DTW]
MRR K=10 の再現率
平均値との差、K=10 で、編集距離は 0.9874 の再現率
→ 同じ音楽データの部分の歌声はそれほど違わないのではないか
24

![[論文紹介]
A Subsequence Matching with Gaps-Range-
Tolerances Framework:
A Query-By-Humming Application
システム情報科学府?情報学専攻
修士1年?池田研究室
ルトフィアナ?サリ?アリスティン
2012 年 12 月 18 日 (火)
情報演習発表
1](https://image.slidesharecdn.com/sari-121210064855-phpapp02/85/Sari-v-1-1-1-320.jpg)

![論文紹介
[タイトル]
A Subsequence Matching with Gaps-Range-Tolerances
Framework: A Query-By-Humming Application
[著者]
Alexios Kotsifakos, Panagiotis Papapetrou, Jaakko Hollmén,
Dimitrios Gunopulos
[書誌情報]
Proceeding of the VLDB Endowment, Vol. 4, No. 11 2011
[概要]
データ処理の観点からハミング検索の問題を解決する.ユーザが
歌ったクエリと音楽データを完全一致させるのではなく、許容範
囲内を設定することで一致条件をあげる.
6](https://image.slidesharecdn.com/sari-121210064855-phpapp02/85/Sari-v-1-1-6-320.jpg)

![問題定式化のための定義
音楽データ: X = {x1 , ..., xn }
クエリは音楽データと同様
音楽データの長さ :|X|
p Q = {q1 , ..., qm }
xj =< x j , xr
j >∈ X p r
|Q|, qi =< qi , qi >∈ X
DB = {X1 , ..., XN }
Q[ts : te] = {qts , ..., qte }
X[ts : te] = {xts , ..., xte }
定義 1
p
qi ≈f xj とは = {f , f } という許容の条件下で
p r f (i) = fp (qi )
p
qi ∈ Q と xj ∈ X が一致するとする f (i, j) = fr (qi , xr )
p
r
j
定義 2
同じ長さの Q[ts1 : te1 ] と X[ts2 : te2 ] に対し、 i ≈f xj
q ?πi ∈ GQ
SM BGT (Q, X) ? te2 ? ts2 ≤ r は下記を満たす: ?γj ∈ GX
f
qi ≈ xj ∧ πi+1 ? πi ? 1 ≤ β, γj+1 ? γj ? 1 ≤ α i = 1, ..., |GQ |
11](https://image.slidesharecdn.com/sari-121210064855-phpapp02/85/Sari-v-1-1-11-320.jpg)
![问题定式化のための定义(例)
Q = {6, 3, 10, 5, 3, 2, 9}, X = {1, 1, 3, 4, 6, 9, 2, 3, 1}
Q[2 : 6] ∧ GQ = {2, 4, 5, 6} ? {3, 5, 3, 2}
X[3 : 8] ∧ GX = {3, 4, 7, 8} ? {3, 4, 2, 3}
次のパラメータを設定する: = 1, α = 2, β = 1, r = 6
{3, 5, 3, 2} vs {3, 4, 2, 3}
α = 2 → {3, , , 2}
{Q[2 : 6], X[3 : 8]} は SM BGT (Q, X)
β = 1 → {3, , 2, }
問題の定式
|SM BGT (Q, Xi [ts : te])| ≥ δ の条件下で
トップ K の S = {Xi [ts : te]|Xi ∈ DB} 見つける
δ は正の整数
12](https://image.slidesharecdn.com/sari-121210064855-phpapp02/85/Sari-v-1-1-12-320.jpg)




![発表者の実験
評価方法
再現率:何%のクエリの正解結果がトップ K 個に入ったか
MRR (Mean Reciprocal Rank):ランクの平均逆数
N
1
1
M RR =
N n=1 rankn
様々な前処理で行った結果
1.000
0.875
0.750
0.625
0.500
0.375
0.250
0.125
0
最低音との差 [ED] 最低音との差 [DTW] Vocaloid [ED] Vocaloid [DTW] 平均値との差 [ED] 平均値との差 [DTW] 中央値との差 [ED] 中央値との差 [DTW]
MRR K=10 の再現率
平均値との差で、編集距離も DTW も K=10 で 0.9098 の再現率
→前処理が重要なのではないか
23](https://image.slidesharecdn.com/sari-121210064855-phpapp02/85/Sari-v-1-1-23-320.jpg)
![発表者の実験
同じ音楽データの部分の歌声はどの程度違うか?
クエリのデータセット→ 50% ターゲットとし、50% 検索クエリとした
様々な前処理で行った歌声-歌声の結果
1.000
0.875
0.750
0.625
0.500
0.375
0.250
0.125
0
最低音との差 [ED] 最低音との差 [DTW] 平均値との差 [ED] 平均値との差 [DTW] 中央値との差 [ED] 中央値との差 [DTW]
MRR K=10 の再現率
平均値との差、K=10 で、編集距離は 0.9874 の再現率
→ 同じ音楽データの部分の歌声はそれほど違わないのではないか
24](https://image.slidesharecdn.com/sari-121210064855-phpapp02/85/Sari-v-1-1-24-320.jpg)

