�ݺ�ߣ

Suatu anggapan yang mungkin benar dan
sering digunakan sebagai dasar pembuatan
keputusan/ pemecahan masalah atau untuk
dasar penelitian lebih lanjut.
Suatu Hipotesis bisa juga salah untuk itu
harus diuji terlebih dahulu dengan
menggunakan data-data observasi

HIPOTESIS
• HIPOTESIS ADALAH PERNYATAAN YANG MASIH LEMAH
TINGKAT KEBENARANNYA SEHINGGA MASIH HARUS DIUJI
MENGGUNAKAN TEKNIK TERTENTU
• HIPOTESIS DIRUMUSKAN BERDASARKAN TEORI, DUGAAN,• HIPOTESIS DIRUMUSKAN BERDASARKAN TEORI, DUGAAN,
PENGALAMAN PRIBADI/ORANG LAIN, KESAN UMUM,
KESIMPULAN YANG MASIH SANGAT SEMENTARA
• HIPOTESIS ADALAH JAWABAN TEORITIK ATAU DEDUKTIF
DAN BERSIFAT SEMENTARA

HIPOTESIS ADALAH PERNYATAAN KEADAAN
POPULASI YANG AKAN DIUJI
KEBENARANNYA MENGGUNAKAN
DATA/INFORMASI YANG DIKUMPULKAN
MELALUI SAMPELMELALUI SAMPEL
JIKA PERNYATAAN DIBUAT UNTUK
MENJELASKAN NILAI PARAMETER POPULASI,
MAKA DISEBUT HIPOTESIS STATISTIK

RUMUSAN HIPOTESIS SEBENARNYA SUDAH DAPAT
DIBACA DARI URAIAN MASALAH, TUJUAN
PENELITIAN, KAJIAN TEORITIK, DAN KERANGKA
PIKIR SEHINGGA RUMUSANNYA HARUS SEJALAN
RUMUSAN HIPOTESIS SEBAGAI PETUNJUK ARAH
DALAM RANCANGAN PENELITIAN, TEKNIK
PENGUMPULAN DAN ANALISIS DATA SERTA
PENYIMPULAN

DINYATAKAN SEBAGAI KALIMAT PERNYATAAN
(DEKLARATIF)
MELIBATKAN MINIMAL DUA VARIABEL PENELITIANMELIBATKAN MINIMAL DUA VARIABEL PENELITIAN
MENGANDUNG SUATU PREDIKSI
HARUS DAPAT DIUJI (TESTABLE)

HIPOTESIS KORELATIF YAITU PERNYATAAN
TENTANG ADA ATAU TIDAK ADANYA HUBUNGAN
ANTARA DUA VARIABEL ATAU LEBIH
HIPOTESIS KOMPARATIF YAITU PERNYATAAN
TENTANG ADA ATAU TIDAK ADANYA PERBEDAAN
ANTARA DUA KELOMPOK ATAU LEBIH

HIPOTESIS NIHIL/NOL (H0) YAITU HIPOTESIS YANG
MENYATAKAN TIDAK ADANYA HUBUNGAN
ANTARA DUA VARIABEL ATAU LEBIH ATAU TIDAK
ADANYA PERBEDAAN ANTARA DUA KELOMPOK
ATAU LEBIHATAU LEBIH
HIPOTESIS ALTERNATIF (H1) YAITU HIPOTESIS
YANG MENYATAKAN ADANYA HUBUNGAN
ANTARA DUA VARIABEL ATAU LEBIH ATAU
ADANYA PERBEDAAN ANTARA DUA KELOMPOK
ATAU LEBIH

KESIMPULANKESIMPULAN HIPOTESISHIPOTESIS
BENARBENAR
HIPOTESISHIPOTESIS
SALAHSALAH
TERIMATERIMA
HIPOTESISHIPOTESIS
KEKELIRUANKEKELIRUAN
MACAM II (MACAM II (ββ))HIPOTESISHIPOTESIS MACAM II (MACAM II (ββ))
(kuasa uji = 1(kuasa uji = 1 –– ββ))
TOLAKTOLAK
HIPOTESISHIPOTESIS
KEKELIRUANKEKELIRUAN
MACAM IMACAM I
(taraf(taraf signifikansisignifikansi αα))

Pembuat keputusan berusaha agar
kedua jenis kesalahan tersebut ditekan
sampai sekecil-kecilnya, hal ni dapat
terjadi jika n meningkat
(sampel makin besar). Kelemahannya
memperbesar sampel berarti
menambah biaya

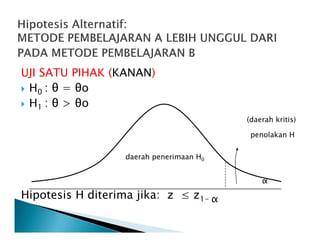
UJI SATU PIHAK (KANAN)
H0 : θ = θo
H1 : θ > θo
(daerah kritis)(daerah kritis)
penolakan H
daerah penerimaan H0
α
Hipotesis H diterima jika: z ≤ z1- α

UJI SATU PIHAK (KIRI)
H0 : θ = θo
H1 : θ < θo
(daerah kritis)
penolakan Hpenolakan H
α
Hipotesis H diterima jika: z ≥ z1- α

UJI DUA PIHAK
H0 : θ = θo
H1 : θ ≠ θo
penolakan H0 penolakan H
½ α ½ α
Hipotesis H diterima jika: -z1/2(1- α) < z < z1/2(1- α)

Pengujian Hipotesis
tentang Rata-rata
Seringkali seorang pembuat keputusan mempunyai
pendapat mengenai nilai rata-rata µ, anggapan
/pendapat yang merupakan hipotesis, apabila akan
dipergunakan untuk membuat keputusan harus diujidipergunakan untuk membuat keputusan harus diuji
terlebih dahulu
Urutan dalam pengujian hipotesis tentang satu rata-rata:
• Rumuskan Hipotesis
• Tentukan nilai
• Hitung Z0
• Pengujian hipotesis dan penarikan kesimpulan
α

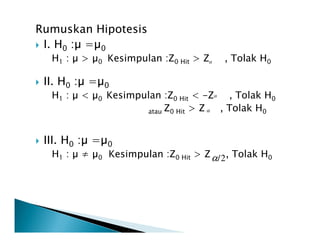
Rumuskan Hipotesis
I. H0 : = 0
H1 : > 0 Kesimpulan :Z0 Hit > Z , Tolak H0
II. H0 : = 0
H1 : < 0 Kesimpulan :Z0 Hit < -Z , Tolak H0
atau Z0 Hit > Z , Tolak H0
α
α
α
III. H0 : = 0
H1 : ≠ 0 Kesimpulan :Z0 Hit > Z , Tolak H02/α

Sampel Besar : n > 30
Menggunakan Uji Z, Varian/ragam diketahui,
dimana
Z hitung =
Sampel Kecil : n < 30
Menggunakan Uji t, varian/ragam diketahui
t hitung =
n
X
X /
0
σ
µ−
ns
X
/
0µ−

Contoh Pengujian Hipotesis satu Rata-rata
• Sebuah penelitian terhadap nilai mata pelajaran
Bahasa Inggris di kelas 8 SMP menunjukkan rata-rata
awal nilai siswa adalah 60 dengan standar deviasi
sebesar 7. Sesudah berselang 3 bulan, guru
meragukan hipotesis ttg rata-rata nilaibahasa Inggris
di atas. Untuk meyakinkan keabsahan hipotesis,di atas. Untuk meyakinkan keabsahan hipotesis,
sebuah sampel diambil secara acak sebesar 40 siswa
dari populasi dan hasilnya ternyata sebesar 73, dan
standar deviasi tidak berubah. Ujilah rata-rata nilai
mata pelajaran bahasa Ingrris siswa tsb memang
lebih besar dari 60?

Dik :H0 : µX = 60
H1 : µX > 60
= 0,05
Z tabel = 1,645
Dit : Ujilah hipotesis tersebut?
Penyelesaian :
Z hitung =
α
X 0
σ
µ−Z hitung =
= 11,8
Karena Z hitung > Z tabel maka Tolak H0
Artinya :Memang benar bahwa hasil sampel dengan hipotesis
menunjukkan bahwa lebih dari 60
nX /σ

Secara hipotesis, mesin stensil ‘Stavo’ dapat
menstensil 6500 helai kertas per jam.
Sebuah perusahaan stensil ingin
membuktikan keabsahan hipotesis di atas.
Perusahaan mengadakan observasi secara
empiris dengan menggunakan 12 mesin
‘Stavo’ dan hasil observasi sbb:
6000 5900 6200 6200 50006000 5900 6200 6200 5000
6100 5800 6400 6500 5400
6200 6700
Apakah hipotesis tersebut dapat dipercaya
atau tidak ?

Diketahui :
H0 : X = 6500
H1 : X ≠ 6500
= 0,05
t hitung =
= 6033, s = 384,06
t tabel = ( , n-1)
α
ns
X
/
0µ−
x
t tabel = ( , n-1)
Penyelesaian:
t hitung =
= -4,13
t tabel = (0,025 , 11)= 2,201
Dengan demikian thitung < t tabel maka terima
H0 Artinya = kemampuan mesin stensil ‘Stavo’
menstensil kertas perjam sama dengan 6500
12/06,384
65006033 −
2/α

�ݺ�ߣ

Uji hipotesis dan uji hipotesis 1_ratarata

Recommended

More Related Content

What's hot (20)

Viewers also liked (11)

Similar to Uji hipotesis dan uji hipotesis 1_ratarata (20)

More from ratuilma (8)

Uji hipotesis dan uji hipotesis 1_ratarata