骋础搁颁贬厂碍モデルを用いた条件付き固有モーメントの実証分析
- 2. 【1】 研究の背景?目的 【2】 先行研究の整理 【3】 分析手法 (GARCHSK Model) 【4】 実証分析 【5】 まとめ アウトライン
- 4. 平均 分散 歪度 尖度 固有平均 固有分散 固有歪度 固有尖度 条件なし 条件付き 【1】 研究の目的 ?日本株式市場を対象に各次数の無条件/条件付きモーメントおよび 固有モーメントと、将来のパフォーマンスとの関係について包括的に分析、 整理する。 将来パフォーマンスとの関係 正比例?反比例?無関係 ???
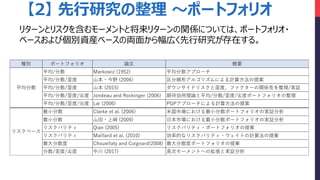
- 5. 【2】 先行研究の整理 ~ポートフォリオ リターンとリスクを含むモーメントと将来リターンの関係については、ポートフォリオ? ベースおよび個別資産ベースの両面から幅広く先行研究が存在する。 種別 ポートフォリオ 論文 概要 平均/分散 Markowiz (1952) 平均分散アプローチ 平均/分散/歪度 山本?今野 (2006) 区分線形アルゴリズムによる計算方法の提案 平均/分散/歪度 山本 (2015) ダウンサイドリスクと歪度、ファクターの関係性を整理/実証 平均/分散/歪度/尖度 Jondeau and Rockinger (2006) 期待効用理論と平均/分散/歪度/尖度ポートフォリオの整理 平均/分散/歪度/尖度 Lai (2006) PGPアプローチによる計算方法の提案 最小分散 Clarke et al. (2006) 米国市場における最小分散ポートフォリオの実証分析 最小分散 山田?上崎 (2009) 日本市場における最小分散ポートフォリオの実証分析 リスクパリティ Qian (2005) リスクパリティ?ポートフォリオの提案 リスクパリティ Maillard et al. (2010) 効率的なリスクパリティ?ウェイトの計算法の提案 最大分散度 Choueifaty and Coignard(2008) 最大分散度ポートフォリオの提案 分散/歪度/尖度 中川 (2017) 高次モーメントへの拡張と実証分析 平均分散 リスクベース
- 6. 【2】 先行研究の整理 ~個別資産 期待効用理論によると、リスク回避的な投資家は奇数次のモーメントは正、偶数次 のモーメントは負の効用。Scott and Horvath (1980) ? ? ? ≈ ? ? ? ? 1 2! ? 2 ? ? ??? ? + 1 3! ? 3 ? ? ???? ? ? 1 4! ? 4 ? ? ???? ? + ? 過去のデータから求めたモーメントが将来の良い推定値(期待値)であるなら 次の関係が成立するはずである。 モーメント 効用関数の符号(選好) 将来リターンとの関係 ボラティリティ 負(大→プレミアムを要求) 大きいほうが高リターン(正比例) 歪度 正(小→プレミアムを要求) 小さいほうが高リターン(反比例) 尖度 負(大→プレミアムを要求) 大きいほうが高リターン(正比例)
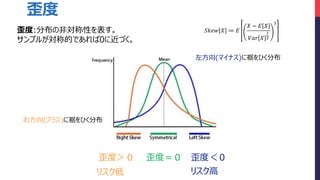
- 7. 左方向(マイナス)に裾をひく分布 右方向(プラス)に裾をひく分布 ???? ? ? ? ? ? ? ? ??? ? 1 2 3 歪度 歪度>0 歪度<0歪度=0 歪度:分布の非対称性を表す。 サンプルが対称的であれば0に近づく。 リスク低 リスク高
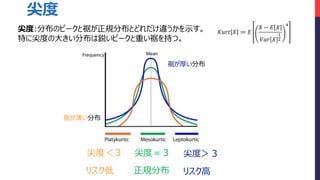
- 8. ???? ? ? ? ? ? ? ? ??? ? 1 2 4 尖度 尖度<3 尖度>3尖度=3 尖度:分布のピークと裾が正規分布とどれだけ違うかを示す。 特に尖度の大きい分布は鋭いピークと重い裾を持つ。 リスク低 リスク高 裾が厚い分布 裾が薄い分布 正規分布
- 9. 【2】 先行研究の整理 ~平均 ①トータルリターン ?長期リバーサル(60カ月):長期的にリターンの低い銘柄のパフォーマンスが良い(反比例) Gutierrez and Pirinsky (2007) ?中期モメンタム(12-1カ月):中期的にリターンの高い銘柄のパフォーマンスが良い(正比例) Jegadeesh and Titman (1993) ?短期リバーサル(1カ月):短期的にリターンの低い銘柄のパフォーマンスが良い(反比例) Lehmann (1990) ②固有リターン???CAPM、APTを前提とするなら無関係 ?中期モメンタム:FF3ファクターによる固有リターンの正比例関係 Blitz et al.(2011) ?短期リバーサル: FF3ファクターを用いた固有リターンの反比例関係 Blitz et al.(2013) ??,? ? ??,? = ?? + ??,??? ? ???,? ? ??,? + ??,??? ????,? + ??,??? ? ???,? + ??,?① ②
- 10. 【2】 先行研究の整理 ~分散 ①ボラティリティ???ハイリスク?ハイリターン(正比例) ?ボラティリティの低い銘柄でも収益率は変わらないという低ボラティリティ効果が報告(反比例) Blitz and van Vliet (2007)、山田?上崎(2009) ?ボラティリティと将来リターンには明確な関係がない(無関係) Amaya et al. (2011) ②固有ボラティリティ???Merton(1987)の枠組みだとハイリスク?ハイリターン(正比例) ?固有ボラティリティが高い銘柄ほど将来リターンが低い固有低ボラティリティ効果(反比例) Ang et al.(2006)、Ang et al.(2009) ?ボラティリティの計測を条件付きモデルのEGARCHモデルにすると効果は消える。(正比例) Fu (2009)、Huang et al.(2010) ?長期リバーサル効果を調整すると有意ではなくなる。 廣瀬?岩永(2011)
- 11. 【2】 先行研究の整理 ~歪度 ①歪度???低歪度?高リターン(反比例) ?歪度と将来リターンに負の相関関係があることを報告(反比例)。 Zhang(2005)、Amaya et al. (2011)、岩澤?内山(2013) ②固有歪度 ?固有歪度と将来リターンに負の相関関係があることを報告(反比例)。 Boyer et al. (2011)、吉野他(2012)
- 12. 【2】 先行研究の整理 ~尖度 ①尖度???高尖度?高リターン(正比例) ?尖度とリターンに正の関係があることを確認した(正比例)。 Amaya et al. (2011) ②固有尖度 ?CAPMによる固有尖度とリターンに負の相関関係があることを確認した(反比例)。 Blau and Whitby (2017)
- 13. 【2】 先行研究の整理 ?本研究では、日本株式市場を対象に すべてモーメント、固有モーメントと将来リター ンの関係を検証。 ?特に、Fu(2009)やHuang et al.(2010) と同様にモーメントの推定手法が与える影 響を見るために、条件付きモデルを用いた計 測も行う。条件付きモデルにはGARCHSKモ デルを適用。 モーメント 無条件 条件付き 平均 Gutierrez and Pirinsky (2007) Jegadeesh and Titman (1993) Lehmann (1990) - 分散 Blitz and van Vliet (2007) 山田?上崎 (2009) 廣瀬?岩永 (2011) - 歪度 Zhang (2005) Amaya et al. (2011) 岩澤?内山 (2013) - 尖度 Amaya et al. (2011) - 固有平均 Blitz et al. (2011) Blitz et al. (2013) - 固有分散 Ang et al. (2006) Ang et al. (2009) 廣瀬?岩永 (2011) 岩澤?内山 (2013) Fu (2009) Huang et al. (2009) 固有歪度 Boyer et al. (2009) 吉野他(2012) - 固有尖度 Blau and Whitby (2017) -
- 14. 【3】 分析手法 ~GARCHSK Model (1) GARCHSKモデルの提案 ? Harvey and Siddique(1999)は、歪度に関するパラメータは安定性に欠け るため、平均、分散、歪度を同時に推定するGARCHSモデルを提案。さらにLeon et al. (2005) はGARCHSモデルを、条件付き尖度の変動も明示的に、同時に 捉えることができるように拡張を行った。 ?条件付き歪度、条件付き尖度の変動はGARCH構造と似たわかりやすい構造をも つ。かつ、推定は容易。 ?Gram-Charlier展開を用いてGARCHSKモデルが従う分布を導出。 (2) GARCHSKモデルによる実際の資産価格変動の実証分析 ?株や為替等で条件付き歪度、条件付き尖度の存在が確認された。 Leon et al. (2005)により提案された条件付きモーメントの変動を記述するモデル
- 15. ?? = ln?? ? ln???1 ?? = ????1 + ?? ? ? = ?0 + ?1 ???1 2 + ?2? ??1 ??|???1~?(0, ? ?) GARCHモデルはBollerslev(1986)によって提案された。 資産リターン??の条件付き分散を過去の収益率のショック???1の2乗に、過去の分散 ? ??1の線形和で表現。時点?の資産価格を??として次のように定式化される。 ? ?? ???1 = 1 2?? ? ? ? ? ? 2 ? ? ? < 1 0 < ?0, ?1, ?2 ?1 + ?2 < 1 定常性を満たすための条件 ?1:ショックに対する反応 ?2:ボラティリティの継続性 GARCH Model
- 16. ?? = ln?? ? ln???1 ?? = ????1 + ?? ? ? = ?0 + ?1 ???1 2 + ?2? ??1 ??|???1~?(0, ? ?) ??? ?? ???1 ? ? ?? ? ? ?? ???1 2 ???1 ? ?? ???1 = ????1 + ? ?? ???1 = ????1 GARCHモデルに従う資産リターン??の条件付き分散が? ?であることを確認する。 はじめに資産リターンの条件付き平均? ?? ???1 を求める。 次に資産リターンの条件付き分散??? ?? ???1 を求める。 = ??? ?? ???1 = ? ? = ? ?? ? ????1 ? ? ?? ???1 2 ???1 = ? (???? ?? ???1 )2 ???1 ∴ ??|???1~?(????1, ? ?) GARCH Model
- 17. ?? = ?0 + ?1 ? ??1 3 + ?2 ???1 ? ? = ?0 + ?1 ? ??1 4 + ?2 ? ??1 ? ? = ? ? ? 1 2 ?? ? ?|???1~????(0,1, ??, ? ?) こういう分布があればOK ?? = ln?? ? ln???1 ?? = ????1 + ?? ? ? = ?0 + ?1 ???1 2 + ?2? ??1 Leon et al. (2005)ではGARCHモデルに対して、条件付き歪度??、条件付き尖 度? ?にGARCH構造を加えたモデル(GARCHSKモデル)を提案した。次のように定式 化される。 定常性を満たすための条件 ??|???1~????(0, ? ?, ??, ? ?) ? , ?1 + ?2 < 1 0 < ?0, ?1, ?2, ?0, ?1, ?2 ?1 + ?2, ?1 + ?2 < 1 【3】 分析手法 ~GARCHSK Model
- 18. ??? ?? ???1 = ??? ?? ???1 = ? ? ???? ?? ???1 ? ? ?? ? ? ?? ???1 ??? ?? ???1 1 2 3 ???1 = ? ?? ? ? ?? ???1 ??? ?? ???1 1 2 3 ???1 ? ?? ???1 = ????1 + ? ?? ???1 = ????1 ?? = ????1 + ?? ? ? = ? ? ? 1 2 ?? ? ?|???1~????(0,1, ??, ? ?) ??|???1~????(0, ? ?, ??, ? ?) GARCHSKモデルに従う資産リターン??の条件付き歪度がs ?であることを確認する。 = ? ? ? ? ? ? ? ???1 1 3 ???1 = ? ? ? ? ? ? ? ???1 ??? ? ? ???1 1 2 3 ???1 = ???? ? ? ???1 = ?? ??? ?? ???1 = ? ?より ? ?で割る 【3】 分析手法 ~GARCHSK Model
- 19. ???? ?? ???1 ? ? ?? ? ? ?? ???1 ??? ?? ???1 1 2 4 ???1 = ? ? ? ? ? ?? ???1 ??? ?? ???1 1 2 4 ???1 = ? ? ? ? ? ? ? ???1 1 4 ???1 = ? ? ? ? ? ? ? ???1 ??? ? ? ???1 1 2 4 ???1 = ???? ? ? ???1 = ? ? ??? ?? ???1 = ? ?より ? ?で割る ∴ ??|???1~????(????1, ? ?, ??, ? ?) ??? ?? ???1 = ??? ?? ???1 = ? ? ? ?? ???1 = ????1 + ? ?? ???1 = ????1 ?? = ????1 + ?? ? ? = ? ? ? 1 2 ?? ? ?|???1~????(0,1, ??, ? ?) ??|???1~????(0, ? ?, ??, ? ?) 【3】 分析手法 ~GARCHSK Model GARCHSKモデルに従う資産リターン??の条件付き尖度が? ?であることを確認する。
- 20. ? ? ? ???1 = ? ? ? ?2 ? ? ?? ?? = 1 + ?? 2 3! + ? ? ? 3 2 4! ? ? ? = 1 + ?? 3! ? ? 3 ? 3? ? + ? ? ? 3 4! (? ? 4 ? 6? ? 2 + 3) Chebyshev-Hermite 多項式を用いた Gram-Charlier展開によってGARCHSKモデルの 確率密度関数 ? ? ? ???1 が従う次のような分布を導出した。 ? ? = ? ? ? 1 2 ??より、??のpdfは? ?? ???1 = ? ? 1/2 ? ? ? ???1 、 ? ? ? は標準正規分布の密度関数 定数項を省いた対数尤度関数? ?は次のようにかける。 ? ? = ? 1 2 ln? ? ? 1 2 ? ? 2 + ln ?2 ? ? ? ln?? max ? ? = ?=1 ? ? ? 各パラメータは最尤法により求めることができる。 【3】 分析手法 ~GARCHSK Model
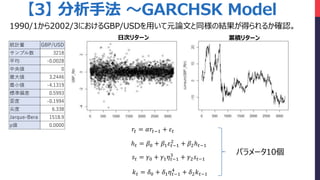
- 21. 統計量 GBP/USD サンプル数 3218 平均 -0.0028 中央値 0 最大値 3.2446 最小値 -4.1319 標準偏差 0.5993 歪度 -0.1994 尖度 6.338 Jarque-Bera 1518.9 p値 0.0000 ?? = ?0 + ?1 ? ??1 3 + ?2 ???1 ? ? = ?0 + ?1 ? ??1 4 + ?2 ? ??1 ?? = ????1 + ?? ? ? = ?0 + ?1 ???1 2 + ?2? ??1 1990/1から2002/3におけるGBP/USDを用いて元論文と同様の結果が得られるか確認。 【3】 分析手法 ~GARCHSK Model 日次リターン 累積リターン パラメータ10個
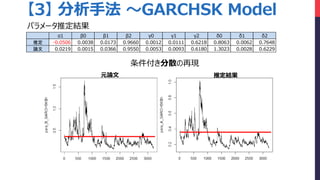
- 22. α1 β0 β1 β2 γ0 γ1 γ2 δ0 δ1 δ2 推定 -0.0506 0.0038 0.0173 0.9660 0.0012 0.0111 0.6218 0.8063 0.0062 0.7648 論文 0.0219 0.0015 0.0366 0.9550 0.0053 0.0093 0.6180 1.3023 0.0028 0.6229 元論文 推定結果 【3】 分析手法 ~GARCHSK Model パラメータ推定結果 条件付き分散の再現
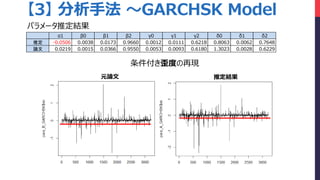
- 23. 元論文 推定結果 【3】 分析手法 ~GARCHSK Model 条件付き歪度の再現 α1 β0 β1 β2 γ0 γ1 γ2 δ0 δ1 δ2 推定 -0.0506 0.0038 0.0173 0.9660 0.0012 0.0111 0.6218 0.8063 0.0062 0.7648 論文 0.0219 0.0015 0.0366 0.9550 0.0053 0.0093 0.6180 1.3023 0.0028 0.6229 パラメータ推定結果
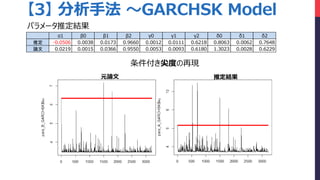
- 24. 元論文 推定結果 【3】 分析手法 ~GARCHSK Model 条件付き尖度の再現 α1 β0 β1 β2 γ0 γ1 γ2 δ0 δ1 δ2 推定 -0.0506 0.0038 0.0173 0.9660 0.0012 0.0111 0.6218 0.8063 0.0062 0.7648 論文 0.0219 0.0015 0.0366 0.9550 0.0053 0.0093 0.6180 1.3023 0.0028 0.6229 パラメータ推定結果
- 25. 【4】 実証分析 TOPIX構成銘柄を対象に各次数の無条件/条件付きモーメントと、将来のパフォーマ ンスの関係を分析。分析対象期間は 1995/6 から 2018/2 までの 273 か月。 無条件 条件付き 無条件 条件付き ① 1 2 5 6 ② 3 4 7 8 各次数のモーメントの計測 リターンの計測 ① ② ?モーメントの計測、リターンの計測の方法により各モーメント8パターンの検証を行う。 ??,? ? ??,? = ?? + ??,??? ? ???,? ? ??,? + ??,??? ????,? + ??,??? ? ???,? + ??,?① ② ?固有モーメント、残差リターンによる計測には、先行研究と整合性をとるため Fama-Franchの3ファクター(FF3)を用いる。
- 26. 1. 毎月末時点のTOPIX 構成銘柄をユニバースとする。 2. 各銘柄の60か月の月次リターンとFF3ファクターの残差リターンから各次数の条件 なしモーメントを計算する。 3. 同時に、60か月の月次リターンとFF3ファクターの残差リターンからGARCHSKモデ ルを推定し、条件付きモーメントを計算する。 4. 無条件、条件付きのそれぞれのモーメントと固有モーメントについて 5 分位ポート フォリオを作成。 5. 各分位ポートフォリオの翌月のリターンは等ウェイトでトータルリターン、FF3 ファク ターの残差リターンを用いて計算する。第 1 分位が特性値 (モーメント) が低い 分位で、第 5 分位が高い分位である。 【4】 実証分析 TOPIX構成銘柄を対象に各次数の無条件/条件付きモーメントと、将来のパフォーマ ンスの関係を分析。分析対象期間は 1995/6 から 2018/2 までの 273 か月。
- 27. ? 評価については、第 1 分位と第 5 分位のリターンの差、絶対リスクの比、シャー プレシオの差を検定する。 ? リターンの差の検定には、等分散性が満たされないことから Welch 法を、絶対リス クの比は F 検定を用いる。 ? 2つのシャープレシオに関する帰無仮説 SR1 = ??2 の両側 ? 値は次のようになる。 2Φ ? |??1 ? ??2| ?? ?? = 1/?(2 1 ? ? + 1/2(??1 + ??2 ? ??1 ??2 ?2)) ここで、 ?はサンプル数、 ???はポートフォリオ ? のシャープレシオ、 ?はポートフォリオのリター ン間の相関係数である。また、 Φ(·) は標準正規分布の累積分布関数を表す。 【4】 実証分析
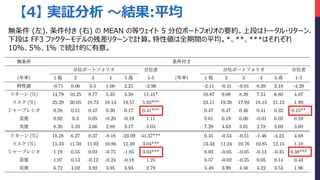
- 28. 【4】 実証分析 ~結果:平均 無条件 (左)、条件付き (右) の MEAN の等ウェイト 5 分位ポートフォリオの要約。上段はトータル?リターン、 下段は FF3 ファクターモデルの残差リターンで計算。特性値は全期間の平均。*、**、***はそれぞれ 10%、5%、1% で統計的に有意。
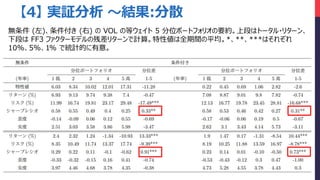
- 29. 【4】 実証分析 ~結果:分散 無条件 (左)、条件付き (右) の VOL の等ウェイト 5 分位ポートフォリオの要約。上段はトータル?リターン、 下段は FF3 ファクターモデルの残差リターンで計算。特性値は全期間の平均。*、**、***はそれぞれ 10%、5%、1% で統計的に有意。
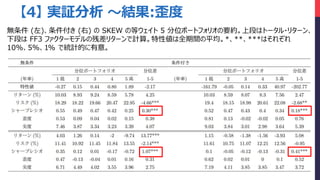
- 30. 【4】 実証分析 ~結果:歪度 無条件 (左)、条件付き (右) の SKEW の等ウェイト 5 分位ポートフォリオの要約。上段はトータル?リターン、 下段は FF3 ファクターモデルの残差リターンで計算。特性値は全期間の平均。*、**、***はそれぞれ 10%、5%、1% で統計的に有意。
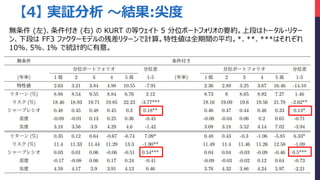
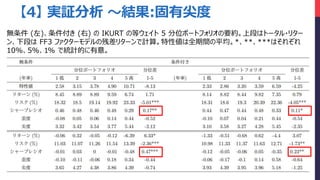
- 31. 【4】 実証分析 ~結果:尖度 無条件 (左)、条件付き (右) の KURT の等ウェイト 5 分位ポートフォリオの要約。上段はトータル?リター ン、下段は FF3 ファクターモデルの残差リターンで計算。特性値は全期間の平均。*、**、***はそれぞれ 10%、5%、1% で統計的に有意。
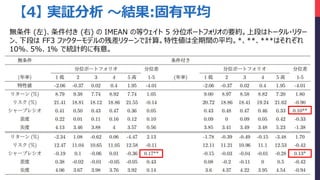
- 32. 【4】 実証分析 ~結果:固有平均 無条件 (左)、条件付き (右) の IMEAN の等ウェイト 5 分位ポートフォリオの要約。上段はトータル?リター ン、下段は FF3 ファクターモデルの残差リターンで計算。特性値は全期間の平均。*、**、***はそれぞれ 10%、5%、1% で統計的に有意。
- 33. 【4】 実証分析 ~結果:固有分散 無条件 (左)、条件付き (右) の IVOL の等ウェイト 5 分位ポートフォリオの要約。上段はトータル?リター ン、下段は FF3 ファクターモデルの残差リターンで計算。特性値は全期間の平均。*、**、***はそれぞ れ 10%、5%、1% で統計的に有意。
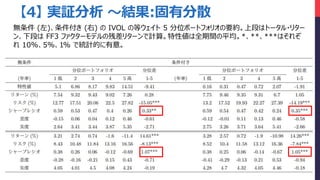
- 34. 【4】 実証分析 ~結果:固有歪度 無条件 (左)、条件付き (右) の ISKEW の等ウェイト 5 分位ポートフォリオの要約。上段はトータル?リター ン、下段は FF3 ファクターモデルの残差リターンで計算。特性値は全期間の平均。*、**、***はそれぞれ 10%、5%、1% で統計的に有意。
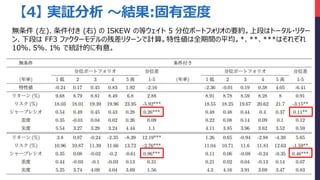
- 35. 無条件 (左)、条件付き (右) の IKURT の等ウェイト 5 分位ポートフォリオの要約。上段はトータル?リター ン、下段は FF3 ファクターモデルの残差リターンで計算。特性値は全期間の平均。*、**、***はそれぞれ 10%、5%、1% で統計的に有意。 【4】 実証分析 ~結果:固有尖度
- 36. ?条件付きで計測すると条件なしの場合に比べて傾向は弱くなるものの、 Fu(2009) 等と異なり依然として反比例関係が成立している。 ?FF3 ファクターの残差リターンで分位ポートフォリオのリターンを計測すると、 さらにその反比例の傾向が強まった。 【5】 まとめ 将来パフォーマンスとの関係 平均 分散 歪度 尖度 固有平均 固有分散 固有歪度 固有尖度 条件なし 反比例 反比例 反比例 反比例 無関係 反比例 反比例 反比例 条件付き 反比例 反比例 反比例 反比例 反比例 反比例 反比例 反比例 ?日本株式市場を対象に各次数の無条件/条件付きモーメントおよび 固有モーメントと、将来のパフォーマンスとの関係について包括的に分析、 整理する。
- 37. 【5】 まとめ ? Fama-MacBeth (1973) のクロスセクション回帰により、どの次 数のモーメント、固有モーメントが有意であるのかを確認する。 ?グローバルな株式市場での検証。