Lecture 3: Unsupervised Learning
- 1. Unsupervised Learning (+ regularization) Sang Jun Lee Ph.D. candidate, POSTECH Email: lsj4u0208@postech.ac.kr EECE695J ņĀäņ×ÉņĀäĻĖ░Ļ│ĄĒĢÖĒŖ╣ļĪĀJ(ļöźļ¤¼ļŗØĻĖ░ņ┤łļ░Åņ▓ĀĻ░ĢĻ│ĄņĀĢņŚÉņØśĒÖ£ņÜ®) ŌĆō LECTURE 3 (2017. 9. 14)
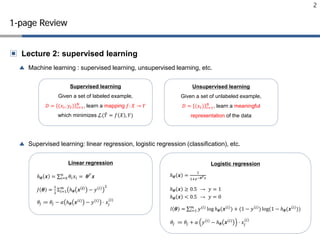
- 2. 2 Ō¢Ż Lecture 2: supervised learning Ō¢▓ Machine learning : supervised learning, unsupervised learning, etc. Ō¢▓ Supervised learning: linear regression, logistic regression (classification), etc. 1-page Review Supervised learning Given a set of labeled example, ØÉĘØÉĘ = (ØæźØæźØæĪØæĪ, Øæ”Øæ”ØæĪØæĪ) ØæĪØæĪ=1 ØæüØæü , learn a mapping ØæōØæō: ØæŗØæŗ ŌåÆ ØæīØæī which minimizes L(’┐ĮØæīØæī = ØæōØæō ØæŗØæŗ , ØæīØæī) Unsupervised learning Given a set of unlabeled example, ØÉĘØÉĘ = (ØæźØæźØæĪØæĪ) ØæĪØæĪ=1 ØæüØæü , learn a meaningful representation of the data Linear regression ŌäÄØ£ĮØ£Į ØÆÖØÆÖ = ŌłæØæ¢Øæ¢=0 ØæøØæø Ø£āØ£āØæ¢Øæ¢ ØæźØæźØæ¢Øæ¢ = Ø£ĮØ£ĮØæćØæć ØÆÖØÆÖ ØÉĮØÉĮ Ø£ĮØ£Į = 1 2 ╬ŻØæ¢Øæ¢=1 ØæÜØæÜ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ ØÆŖØÆŖ ŌłÆ Øæ”Øæ” Øæ¢Øæ¢ 2 Ø£āØ£āØæŚØæŚ Ōēö Ø£āØ£āØæŚØæŚ ŌłÆ Øø╝Øø╝ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ Øæ¢Øæ¢ ŌłÆ Øæ”Øæ” Øæ¢Øæ¢ Ōŗģ ØæźØæźØæŚØæŚ (Øæ¢Øæ¢) ŌäÄØ£ĮØ£Į ØÆÖØÆÖ = 1 1+ØæÆØæÆŌłÆØ£ĮØ£Į ØæćØæć ØÆÖØÆÖ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ Ōēź 0.5 ŌåÆ Øæ”Øæ” = 1 ŌäÄØ£ĮØ£Į ØÆÖØÆÖ < 0.5 ŌåÆ Øæ”Øæ” = 0 ØæÖØæÖ Ø£ĮØ£Į = ŌłæØæ¢Øæ¢=1 ØæÜØæÜ Øæ”Øæ”(Øæ¢Øæ¢) log ŌäÄØ£ĮØ£Į(ØÆÖØÆÖ Øæ¢Øæ¢ ) + (1 ŌłÆ Øæ”Øæ” Øæ¢Øæ¢ ) log(1 ŌłÆ ŌäÄØ£ĮØ£Į(ØÆÖØÆÖ Øæ¢Øæ¢ )) Ø£āØ£āØæŚØæŚ Ōēö Ø£āØ£āØæŚØæŚ + Øø╝Øø╝ Øæ”Øæ” Øæ¢Øæ¢ ŌłÆ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ Øæ¢Øæ¢ Ōŗģ ØæźØæźØæŚØæŚ Øæ¢Øæ¢ Logistic regression
- 3. Ō¢Ż Overfitting? Training dataņŚÉ ņ¦Ćļéśņ╣śĻ▓ī(over) fit ļÉśņ¢┤ ņØ╝ļ░śņĀüņØĖ ņČöņäĖļź╝ Ēæ£ĒśäĒĢśņ¦Ć ļ¬╗ĒĢśļŖö ļ¼ĖņĀ£ ņØ╝ļ░śņĀüņ£╝ļĪ£ ĒĢÖņŖĄļŹ░ņØ┤Ēä░ņŚÉ ņ¦Ćļéśņ╣śĻ▓ī ĒÄĖĒ¢źļÉ£ ļ│Ąņ×ĪĒĢ£ ļ¬©ļŹĖ(ļČłĒĢäņÜöĒĢ£ curve)ļĪ£ ņØĖĒĢśņŚ¼ ļ░£ņāØ Ō¢Ż OverfittingņØä ņżäņØ┤ĻĖ░ ņ£äĒĢ£ ļ░®ļ▓Ģ Ō¢▓ Reduce the number of parameters (ļŹ░ņØ┤Ēä░ļź╝ Ēæ£ĒśäĒĢśļŖö feature vectorļź╝ ĒÜ©Ļ│╝ņĀüņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢ©ņ£╝ļĪ£ņŹ© dataņØś dimension ņČĢņåī) Ō¢▓ Regularization (cost function) 3 The problem of overfitting ņĀüņĀłĒĢ£ hypothesis functionņØĆ ļŗ©ņł£ĒĢĀ ĒĢ©ņłśņØ╝ Ļ▓āņØ┤ļØ╝ļŖö Ļ░ĆņĀĢ
- 4. Ō¢Ż Regularization ParameterņØś Ļ░£ņłśļź╝ ņ£Āņ¦ĆĒĢśļÉś Ēü¼ĻĖ░ļź╝ Ļ░Éņåīņŗ£Ēé┤ņ£╝ļĪ£ņŹ© overfittingņØä Ēö╝ĒĢśļŖö ļ░®ļ▓Ģ Housing price prediction ļ¼ĖņĀ£ņŚÉņä£ņØś hypothesis function: ŌäÄØ£ĮØ£Į ØÆÖØÆÖ = Ø£āØ£ā0 + Ø£āØ£ā1 ØæźØæź1 + Ø£āØ£ā2 ØæźØæź2 ļ¬©ļŹĖņŚÉ ļö░ļØ╝ under-fitting (high bias) ļśÉļŖö overfitting (high variance)ņØś ļ¼ĖņĀ£Ļ░Ć ļ░£ņāØĒĢĀ ņłś ņ׳ļŗż! 4 The problem of overfitting
- 5. Ō¢Ż Regularization Linear regressionņŚÉņä£ņØś cost function: ØÉĮØÉĮ Ø£ĮØ£Į = 1 2ØæÜØæÜ ’┐Į Øæ¢Øæ¢=1 ØæÜØæÜ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ ØÆŖØÆŖ ŌłÆ Øæ”Øæ” Øæ¢Øæ¢ 2 ņ£ä ņŗØņŚÉņä£ parameter Ø£ĮØ£Į ņØś Ēü¼ĻĖ░ļź╝ ņżäņØ┤ļŖö regularization parameter Ø£åØ£åņØś ļÅäņ×ģ Gradient descentņŚÉņä£ update rule: 5 The problem of overfitting ØÉĮØÉĮ Ø£ĮØ£Į = 1 2ØæÜØæÜ ’┐Į Øæ¢Øæ¢=1 ØæÜØæÜ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ ØÆŖØÆŖ ŌłÆ Øæ”Øæ” Øæ¢Øæ¢ 2 + Ø£åØ£å Ōŗģ ’┐Į ØæŚØæŚ=1 ØæøØæø Ø£āØ£āØæŚØæŚ 2 Ø£āØ£ā0 Ōēö Ø£āØ£ā0 ŌłÆ Øø╝Øø╝ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ Øæ¢Øæ¢ ŌłÆ Øæ”Øæ” Øæ¢Øæ¢ Ōŗģ ØæźØæź0 (Øæ¢Øæ¢) Ø£āØ£āØæŚØæŚ Ōēö Ø£āØ£āØæŚØæŚ 1 ŌłÆ Øø╝Øø╝ Ø£åØ£å ØæÜØæÜ ŌłÆ Øø╝Øø╝ 1 ØæÜØæÜ ’┐Į Øæ¢Øæ¢=1 ØæÜØæÜ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ Øæ¢Øæ¢ ŌłÆ Øæ”Øæ” Øæ¢Øæ¢ Ōŗģ ØæźØæźØæŚØæŚ Øæ¢Øæ¢ Ø£āØ£ā0ņØĆ regularize ĒĢśņ¦Ć ņĢŖņØī Update ĒĢĀ ļĢī parameterņØś Ēü¼ĻĖ░ļź╝ Ļ░Éņåīņŗ£ĒéżļŖö ĒÜ©Ļ│╝!
- 6. Ō¢Ż Normal equationņØś ļ│ĆĒÖö Linear regressionņŚÉņä£ņØś normal equation : , where ØæŗØæŗ = ŌłÆØÆÖØÆÖ Ø¤ÅؤŠØæćØæć ŌłÆ Ōŗ« ŌłÆØÆÖØÆÖ ØÆÄØÆÄ ØæćØæć ŌłÆ , Ø£ĮØ£Į = Ø£āØ£ā0 Ōŗ« Ø£āØ£āØæøØæø , and ØÆÜØÆÜ = Øæ”Øæ”(1) Ōŗ« Øæ”Øæ”(ØæÜØæÜ) Regularization parameterļź╝ ļÅäņ×ģĒĢśļ®┤ ņ░ĖĻ│Ā: ØæŗØæŗ ØæćØæć ØæŗØæŗ + Ø£åØ£å Ōŗģ ØÉ╝ØÉ╝ņØś ņŚŁĒ¢ēļĀ¼ņØĆ ĒĢŁņāü ņĪ┤ņ×¼ (Ø£åØ£å > 0) 6 Regularization Positive semi-definiter (if ØæÜØæÜ Ōēż ØæøØæø, ØæŗØæŗ ØæćØæć ØæŗØæŗ is not invertiable) Positive definite
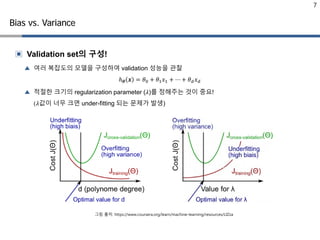
- 7. Ō¢Ż Validation setņØś ĻĄ¼ņä▒! Ō¢▓ ņŚ¼ļ¤¼ ļ│Ąņ×ĪļÅäņØś ļ¬©ļŹĖņØä ĻĄ¼ņä▒ĒĢśņŚ¼ validation ņä▒ļŖźņØä Ļ┤Ćņ░░ ŌäÄØ£ĮØ£Į ØÆÖØÆÖ = Ø£āØ£ā0 + Ø£āØ£ā1 ØæźØæź1 + Ōŗ» + Ø£āØ£āØææØææ ØæźØæźØææØææ Ō¢▓ ņĀüņĀłĒĢ£ Ēü¼ĻĖ░ņØś regularization parameter (Ø£åØ£å)ļź╝ ņĀĢĒĢ┤ņŻ╝ļŖö Ļ▓āņØ┤ ņżæņÜö! (Ø£åØ£åĻ░ÆņØ┤ ļäłļ¼┤ Ēü¼ļ®┤ under-fitting ļÉśļŖö ļ¼ĖņĀ£Ļ░Ć ļ░£ņāØ) 7 Bias vs. Variance ĻĘĖļ”╝ ņČ£ņ▓ś: https://www.coursera.org/learn/machine-learning/resources/LIZza
- 8. 8 Ō¢Ż Clustering ļ╣äņŖĘĒĢ£ ĒŖ╣ņä▒ņØś ļŹ░ņØ┤Ēä░ļōżņØä ļ¼ČļŖö ņĢīĻ│Āļ”¼ņ”ś Ō¢▓ K-means algorithm Ō¢▓ Spectral clustering Ō¢Ż Anomaly detection Ō¢▓ Density estimation Unsupervised learning EECE695J (2017) Sang Jun Lee (POSTECH) K-means ClusterņØś centerļĪ£ļČĆĒä░ņØś Ļ▒░ļ”¼ļź╝ ĻĖ░ņżĆņ£╝ļĪ£ clustering Spectral clustering ØÉ║ØÉ║(ØæēØæē, ØÉĖØÉĖ): vertices and edges ņ¢╝ļ¦łļéś ņĀüņØĆ ļ╣äņÜ®ņ£╝ļĪ£ ĻĘĖļל Ēöäļź╝ partitioning ĒĢĀ Ļ▓āņØĖĻ░Ć
- 9. 9 ņŻ╝ņ¢┤ņ¦ä ØæüØæüĻ░£ņØś ļŹ░ņØ┤Ēä░( ØÆÖØÆÖØÆĢØÆĢ Ōłł ŌäØØÉĘØÉĘ ØæĪØæĪ=1 ØæüØæü )ļź╝ ļīĆĒæ£ĒĢśļŖö ØæśØæśĻ░£ņØś center ØØüØØüØÆŗØÆŗ (ØæŚØæŚ = 1, Ōŗ» , ØÉŠØÉŠ)ļź╝ ņ░ŠļŖö ļ¼ĖņĀ£ ŌåÆ ļŹ░ņØ┤Ēä░ļōżņØä ØæśØæśĻ░£ņØś ĻĘĖļŻ╣ņ£╝ļĪ£ partitioning Initialize ØØüØØüØÆŗØÆŗ (ØæŚØæŚ = 1, Ōŗ» , ØÉŠØÉŠ) Repeat until convergence! K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) Assignment step Assign all data points to the cluster for which ØÆÖØÆÖØÆĢØÆĢ ŌłÆ ØØüØØüØÆŗØÆŗ 2 is smallest Update step Compute new means for every cluster ØØüØØüØÆŗØÆŗ ØÆÅØÆÅØÆÅØÆÅØÆÅØÆÅ = 1 ØæüØæüØæŚØæŚ ╬ŻØæĪØæĪŌłłØÉČØÉČØæŚØæŚ ØÆÖØÆÖØÆĢØÆĢ ņ░ŠņĢäņĢ╝ĒĢśļŖöĻ▓ī optimal clusterņÖĆ optimal meanņØĖļŹ░.. meanņØä Ļ│ĀņĀĢĒĢśņŚ¼ optimal clusterļź╝ ļ©╝ņĀĆ ņ░ŠĻ│Ā ņ░ŠņØĆ optimal cluster ņĢłņŚÉņä£ ņāłļĪ£ņÜ┤ optimal mean Ļ│äņé░ Not optimal solution!
- 10. 10 K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) Initialize
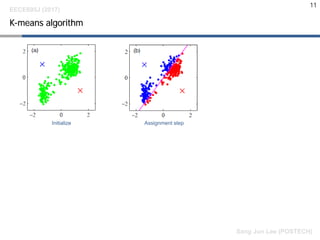
- 11. 11 K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) Initialize Assignment step
- 12. 12 K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) Initialize Assignment step Update step
- 13. 13 K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) Initialize Assignment step Update step Assignment step
- 14. 14 K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) Initialize Assignment step Update step Assignment step Update step
- 15. 15 K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) Initialize Assignment step Update step Assignment step Update step Assignment step
- 16. 16 K-means algorithm in TensorFlow EECE695J (2017) Sang Jun Lee (POSTECH) ipythonņØś ņø╣ņāüņŚÉņä£ ĻĘĖļ”╝ņØä ĻĘĖļ”¼ĻĖ░ ņ£äĒĢ£ ļ¬ģļĀ╣ņ¢┤ ļæÉ Ļ░£ņØś normal distributionņ£╝ļĪ£ sample data ĻĄ¼ņä▒ vectors_set : 2000x2
- 17. 17 K-means algorithm in TensorFlow EECE695J (2017) Sang Jun Lee (POSTECH)
- 18. 18 K-means algorithm in TensorFlow EECE695J (2017) Sang Jun Lee (POSTECH) 2000Ļ░£ņØś ņāśĒöī ņżæ kĻ░£ļź╝ ņ×äņØśļĪ£ ņäĀ ĒāØĒĢśņŚ¼ initial mean Ļ░Æņ£╝ļĪ£ ĒÖ£ņÜ® expanded_vectors: (tensor) 1x2000x2 expanded_centroids: (tensor) 4x1x2
- 19. 19 K-means algorithm in TensorFlow EECE695J (2017) Sang Jun Lee (POSTECH) Assignment Ļ│╝ņĀĢļÅä Ļ░ÆņØ┤ ļōżņ¢┤Ļ░ĆļŖö Ļ▓āņØ┤ ņĢäļŗłļØ╝ ņØ╝ņóģņØś operationņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö graph
- 20. 20 K-means algorithm in TensorFlow EECE695J (2017) Sang Jun Lee (POSTECH) ņŗżņĀ£ ĒĢÖņŖĄĻ│╝ņĀĢ (100ĒÜī ļ░śļ│Ą) K=4 K=2
- 21. 21 Ō¢Ż K-means algorithmņØś ņżæņÜöĒĢ£ ļæÉ Ļ░Ćņ¦Ć ņØ┤ņŖł Ō¢▓ MeanņØś initializationņØä ņ¢┤ļ¢╗Ļ▓ī ĒĢĀ Ļ▓āņØĖĻ░Ć? Random initialization: ŌĆó NĻ░£ņØś ņāśĒöī ņżæ kĻ░£ļź╝ ļ¼┤ņ×æņ£äļĪ£ ļĮæņĢä ņ┤łĻĖ░Ļ░Æņ£╝ļĪ£ ņé¼ņÜ® ŌĆó ņ┤łĻĖ░Ļ░ÆņŚÉ ļö░ļØ╝ clusteringņØś Ļ▓░Ļ│╝Ļ░Ć ņĢłņóŗņØä ņłś ņ׳ņØī ŌĆó Random initialization Ļ│╝ņĀĢņØä ņŚ¼ļ¤¼ ļ▓ł ņłśĒ¢ē Ō¢▓ ClusterņØś Ļ░£ņłś kņØś Ļ▓░ņĀĢ ņØ╝ļ░śņĀüņ£╝ļĪ£ clusterņØś Ļ░£ņłśļź╝ ļŹ░ņØ┤Ēä░ņØś ļČäĒżņŚÉ ļö░ļØ╝ ņé¼ļ×īņØ┤ Ļ▓░ņĀĢĒĢśļŖöļŹ░.. K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) ĻĘĖļ”╝ ņČ£ņ▓ś: https://wikidocs.net/4693
- 22. 22 Ō¢Ż K-means algorithmņØś ņżæņÜöĒĢ£ ļæÉ Ļ░Ćņ¦Ć ņØ┤ņŖł Ō¢▓ ClusterņØś Ļ░£ņłś kņØś Ļ▓░ņĀĢ Elbow method: ŌĆó kĻ░ÆņŚÉ ļö░ļźĖ cost functionņŚÉ ļīĆĒĢ£ ĒĢ©ņłśļź╝ ĻĘĖļĀĖņØä ļĢī, ĒŖ╣ņĀĢ k ņØ┤Ēøä costĻ░Ć ļ│ĆĒÖöĻ░Ć ņĀüņØĆ elbow pointļź╝ kĻ░Æņ£╝ļĪ£ Ļ▓░ņĀĢ ŌĆó kĻ░ÆņŚÉ ļö░ļźĖ cost functionņØś ļ│ĆĒÖöĻ░Ć smooth ĒĢĀ Ļ▓ĮņÜ░ elbow pointļź╝ ņ░ŠĻĖ░ Ēלļōż ņłś ņ׳ļŗż. K-means algorithm EECE695J (2017) Sang Jun Lee (POSTECH) ĻĘĖļ”╝ ņČ£ņ▓ś: https://wikidocs.net/4693
- 23. 23 Ō¢Ż Clustering criteria: Ō¢▓ The affinities of data within the same cluster should be high Ō¢▓ The affinities of data between different clusters should be low Spectral clustering EECE695J (2017) ĻĘĖļ”╝ ņ░ĖņĪ░: POSTECH CSED441 lecture13 ļŹ░ņØ┤Ēä░ ņāśĒöī ņé¼ņØ┤ņØś Ļ┤ĆļĀ©ņä▒
- 24. 24 Optimization objective: AffinityņØś ņ┤Ø ĒĢ®ņØ┤ ņĄ£ļīĆĻ░Ć ļÉśļŖö clusterļź╝ ņ░ŠļŖö Ļ▓āņØ┤ ļ¬®ņĀü (ØÆÖØÆÖ : ļŹ░ņØ┤Ēä░ņØś cluster ņĀĢļ│┤ļź╝ ļéśĒāĆļé┤ļŖö vector) Convert the discrete optimization problem to continuous domain (+ ØæźØæźņØś lengthļĪ£ normalize) Spectral clustering EECE695J (2017) Discrete optimization problem Maximum eigenvalue problem
- 25. 25 Spectral clusteringņØś ļśÉ ļŗżļźĖ ņØ┤ĒĢ┤ Minimum-cut algorithm Spectral clustering EECE695J (2017)
- 26. 26 Minimum-cut algorithm Gaussian similarity function Spectral clustering EECE695J (2017) ØæżØæżØæ¢Øæ¢Øæ¢Øæ¢ = exp{ŌłÆ ØæŻØæŻØæ¢Øæ¢ ŌłÆ ØæŻØæŻØæŚØæŚ 2 2Ø£ÄØ£Ä2 } Diagonal = 1 Off-diagonal Ōēż 1 Affinity matrix ØæøØæø ؤÉØ¤É ├Ś ØæøØæø ؤÉØ¤É matrix
- 27. 27 Objective function: Spectral clustering EECE695J (2017) Reference: POSTECH CSED441 lecture13
- 28. 28 ņ£äņØś ņĄ£ņĀüĒÖö ļ¼ĖņĀ£ļŖö Ļ▓░ĻĄŁ ņĢäļלņÖĆ Ļ░ÖņØĆ eigenvalue problemņ£╝ļĪ£ ļ░öļĆīļŖöļŹ░.. (Unnormalized) graph Laplacian: ŌĆó For every vector ØÆÖØÆÖ Ōłł ŌäØØæøØæø , ØÆÖØÆÖØæćØæć ØÉ┐ØÉ┐ØÆÖØÆÖ = 1 2 ŌłæØæ¢Øæ¢=1 ØæøØæø ŌłæØæŚØæŚ=1 ØæøØæø ØæżØæżØæ¢Øæ¢Øæ¢Øæ¢ ØæźØæźØæ¢Øæ¢ ŌłÆ ØæźØæźØæŚØæŚ 2 Ōēź 0 (positive semi-definite) ŌĆó ØÉ┐ØÉ┐ņØĆ ļŗ© 1Ļ░£ņØś Ø£åØ£å = 0ņØä ļ¦īņĪ▒ĒĢśļŖö eigenvalueļź╝ Ļ░Ćņ¦Ćļ®░, ĻĘĖ ļĢīņØś eigenvectorļŖö ØÆÖØÆÖ = ؤÅؤŠņØ┤ļŗż. ŌĆó ļ¬©ļōĀ ļŹ░ņØ┤Ēä░Ļ░Ć ĒĢśļéśņØś clusterļĪ£ ļ¼ČņØ┤ļŖö Ļ▓āņØĆ ņØśļ»ĖĻ░Ć ņŚåņ£╝ļ»ĆļĪ£.. Minimum-cut algorithmņØś solutionņØĆ second minimum eigenvalueņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö eigenvector Spectral clustering EECE695J (2017) ØÉ┐ØÉ┐ = ØÉĘØÉĘ ŌłÆ ØæŖØæŖ
- 29. 29 Minimum-cut algorithm: ŌĆó Find the second minimum eigenvector of ØÉ┐ØÉ┐ = ØÉĘØÉĘ ŌłÆ ØæŖØæŖ ŌĆó Partition the second minimum eigenvector ņ░ĖĻ│Ā: Two moon dataņŚÉņä£ņØś second minimum eigenvector ņ░ĖĻ│Ā: Minimum-cut algorithmņØĆ optimal solutionņØä ņ░ŠļŖö Ļ▓āņØ┤ ņĢäļŗłļØ╝ optimal solutionņØś approximationņØä ņ░ŠļŖöļŗż Spectral clustering EECE695J (2017) Second smallest eigenvector
- 30. 30 K-means ŌĆó ņĢīĻ│Āļ”¼ņ”śņØ┤ Ļ░äļŗ©! ŌĆó ņ┤łĻĖ░Ļ░ÆņŚÉ ļö░ļźĖ ņĢīĻ│Āļ”¼ņ”ś Ļ▓░Ļ│╝ņØś ļ│ĆļÅÖņä▒ Spectral clustering ŌĆó Ļ│äņé░ļ¤ēņØ┤ ļ¦ÄņØī ŌĆó ļŹ░ņØ┤Ēä░ņØś clusterĻ░Ć highly non-convexņØ╝ ļĢī ĒÜ©Ļ│╝ņĀü! ŌĆó ļÅÖņØ╝ ļŹ░ņØ┤Ēä░ņŚÉ ļīĆĒĢśņŚ¼ ļ╣äņŖĘĒĢ£ Ļ▓░Ļ│╝ ļÅäņČ£ K-means vs. spectral clustering EECE695J (2017) Reference: POSTECH Machine Learning lecture8 K-means Spectral clustering
- 31. 31 ņØ╝ļ░śņĀüņØĖ ļŹ░ņØ┤Ēä░Ļ░Ć Ēīīļ×ĆņāēĻ│╝ Ļ░ÖņØĆ ļČäĒżļź╝ Ļ░Ćņ¦ł ļĢī, (ļ╣©Ļ░äņāē ņĀÉļōżĻ│╝ Ļ░ÖņØ┤) ņØ┤ņāüĒĢ£ ļŹ░ņØ┤Ēä░ļōżņØä Ļ▓ĆņČ£ĒĢ┤ļé┤ļŖö ļ░®ļ▓Ģ? Anomaly detection EECE695J (2017)
- 32. 32 ņØ╝ļ░śņĀüņØĖ ļŹ░ņØ┤Ēä░Ļ░Ć Ēīīļ×ĆņāēĻ│╝ Ļ░ÖņØĆ ļČäĒżļź╝ Ļ░Ćņ¦ł ļĢī, (ļ╣©Ļ░äņāē ņĀÉļōżĻ│╝ Ļ░ÖņØ┤) ņØ┤ņāüĒĢ£ ļŹ░ņØ┤Ēä░ļōżņØä Ļ▓ĆņČ£ĒĢ┤ļé┤ļŖö ļ░®ļ▓Ģ? Density estimation using multivariate Gaussian distribution Anomaly detection EECE695J (2017)
- 33. 33 Density estimation using multivariate Gaussian distribution Parameter fitting: Given training set {ØæźØæź Øæ¢Øæ¢ Ōłł ŌäØØæøØæø : Øæ¢Øæ¢ = 1, Ōŗ» , ØæÜØæÜ} Ø£ćØ£ć = 1 ØæÜØæÜ ’┐Į Øæ¢Øæ¢=1 ØæÜØæÜ ØæźØæź(Øæ¢Øæ¢) ╬Ż = 1 ØæÜØæÜ ’┐Į Øæ¢Øæ¢=1 ØæÜØæÜ ØæźØæź Øæ¢Øæ¢ ŌłÆ Ø£ćØ£ć ØæźØæź Øæ¢Øæ¢ ŌłÆ Ø£ćØ£ć ØæćØæć Anomaly if ØæØØæØ ØæźØæź; Ø£ćØ£ć, ╬Ż < Ø£¢Ø£¢ for given Ø£¢Ø£¢ Anomaly detection EECE695J (2017)
- 34. 34 Density estimation using multivariate Gaussian distribution Anomaly detection EECE695J (2017)
- 35. 35 Ō¢▓ Regularization for preventing overfitting Ō¢▓ Unsupervised learning ŌĆó Clustering: k-means, spectral clustering ŌĆó Anomaly detection (density estimation) Summary
- 36. 36 Date: 2017. 9. 21 (Thur) Time: 14:00-15:15 Ō¢Ż Introduction to neural networks Ō¢▓ Basic structure of neural networks: linear transformation, activation functions Ō¢▓ Implementation of neural network in Python and TensorFlow Preview (Lecture 4)







































![[ĻĖ░ņ┤łĻ░£ļģÉ] Graph Convolutional Network (GCN)](https://cdn.slidesharecdn.com/ss_thumbnails/agistdkimgcn190507-190507153736-thumbnail.jpg?width=560&fit=bounds)












![[ĒĢ£ĻĖĆ] Tutorial: Sparse variational dropout](https://cdn.slidesharecdn.com/ss_thumbnails/tutorialsparsevariationaldropout-190728122300-thumbnail.jpg?width=560&fit=bounds)














![[SOPT] ļŹ░ņØ┤Ēä░ ĻĄ¼ņĪ░ ļ░Å ņĢīĻ│Āļ”¼ņ”ś ņŖżĒä░ļöö - #01 : Ļ░£ņÜö, ņĀÉĻĘ╝ņĀü ļ│Ąņ×ĪļÅä, ļ░░ņŚ┤, ņŚ░Ļ▓░ļ”¼ņŖżĒŖĖ](https://cdn.slidesharecdn.com/ss_thumbnails/1-150824001021-lva1-app6892-thumbnail.jpg?width=560&fit=bounds)









![[Probability for machine learning]](https://cdn.slidesharecdn.com/ss_thumbnails/probabilityformachinelearning-180726131331-thumbnail.jpg?width=560&fit=bounds)



