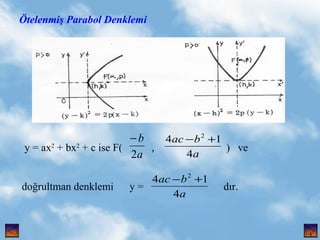
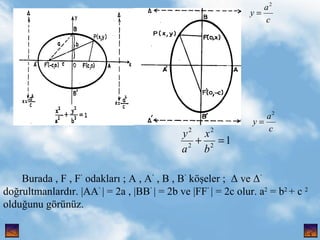
2. KON?KLER Tan?m: Sabit bir noktas? F ve sabit bir do?rusu Δ olan bir Π düzleminin (P) = {P:|PF| = |PH| , Δ , F , P Π } noktalar?n?n kümesine parabol denir. Burada F odak,O tepe(k??e), Δ do?rultman,2p parametre ve parabolün simetrik oldu?u do?ru da eksen ad?n? al?r.Ekseni X ve Y,k??esi ba?lang?? noktas? olan parabolleri g?rüyorsunuz. ,
4. Parabol Ve Do?ru y 2 = 2px parabolü ile y = m.x + n do?rusu kesi?ti?inde ( m.x + n ) 2 = 2px denkleminden kesim noktalar?n?n apsisleri bulunur.Burada : p - 2mn < 0 durumunda do?ru parabolü kesmez. P - 2mn > 0 durumunda do?ru parabolü farkl? 2 noktada keser. P - 2mn = 0 durumunda do?ru parabole te?et olur(de?me ko?ulu). De?me Noktas? ( ) olur. Parabole Bir Noktadan ?izilen Te?et Denklemi Parabol ve (x 0 , y 0 ) noktas? verilsin.Bu noktadaki te?et denklemi : ,
5. y 2 = 2px i?in yy 0 = p( x + x 0 ) x 2 = 2py i?in xx 0 = p( y + y 0 ) d?r. Parabolün K??egeni E?imleri ayn? olan kiri?lerin orta noktalar?n?n kümesine k??egen denir. y 2 = 2px parabolünün e?imi m olan kiri?lerinin orta noktalar?n? kümesi y=p / m olur. y = p / m do?rusu ,e?imi m olan te?etin de?me noktas?ndan ge?er. y = p / m do?rusuna ve e?imi m olan kiri?lere birbirinin e?leni?i denir. EL?PS Tan?m: π düzleminin farkl? ve sabit iki noktas? F , F ’ ; de?i?en bir noktas? P ise düzlemin P noktalar?n?n (E) = {P,|PF| + |PF ’ | = 2a , F , F ’ , p π , a > c > 0 , |FF ’ | = 2c} kümesine elips denir. ,
6. Burada , F , F ’ odaklar? ; A , A ’ , B , B ’ k??eler ; Δ ve Δ ’ do?rultmanlard?r. |AA ’ | = 2a , |BB ’ | = 2b ve |FF ’ | = 2c olur. a 2 = b 2 + c 2 oldu?unu g?rünüz. ,
7. Elips Ve Do?ru elipsi ile y = m.x + n do?rusunun kesi?meleri durumu : a 2 m 2 + b 2 - n 2 > 0 ise iki farkl? noktada kesi?irler. a 2 m 2 + b 2 - n 2 < 0 ise kesi?mezler. a 2 m 2 + b 2 - n 2 = 0 ise bir noktada keser, te?et olur(de?me ko?ulu). De?me noktas? ise d?r. Elipse Bir Noktas?ndan ?izilen Te?et Denklemi Elips merkezinden ge?en kiri?lere elipsin k??egeni denir. ,
8. E?imleri aras?nda m 1 . m 2 = ba??nt?s? bulunan iki k??egene e?lenik k??egenler ad? verilir., y = m.x k??egeninin e?leni?i olur. Elipsin Parametresi Elipsin odaklar?ndan birinden eksene ?izilen dik kiri? uzunlu?una parametre denir. Parametre = 2p = d?r. Elipsin D??merkezli?i Elipste d??merkezlik oran?na verilen add?r. e < 1 d?r. Elipsi Alan? elipsinin alan? πab d?r. ,
9. H?PERBOL Tan?m: π düzleminin sabit iki noktas? F , F ’ ve herhangi bir noktas? P ise P noktalar?n?n ; ( H ) = { P : [|PF | - |PF ’ | = 2a , |FF ’ | = 2c , a < c , F , F ’ , F π } kümesine hiperbol denir. Burada ; F , F ’ odaklar ; A , A ’ , B , B ’ k??eler ; Δ ve Δ do?rultmanlard?r. a 2 = a 2 + b 2 oldu?unu g?rüyorsunuz. ,
11. n 2 + b 2 - a 2 m 2 > 0 ise do?ru hiperbolü iki noktada keser. n 2 + b 2 - a 2 m 2 <0 ise do?ru hiperbolü kesmez. n 2 + b 2 - a 2 m 2 = 0 ise do?ru hiperbole te?et olur (de?me ko?ulu) De?me noktas? da d?r. Hiperbole Bir Noktas?ndan ?izilen Te?et Denklemi Hiperbol ve P ( x 0 , y 0 ) noktas? verilsin.Bu noktadaki te?et denklemi : i?in i?in d?r. ,
12. Hiperbolün K??egeni Hiperbolün merkezinden ge?en do?rulara k??egen denir.E?imleri aras?nda m 1 .m 2 = ba??nt?s? bulunan y = m.x ve y = . X k??elerine de e?lenik k??egenler ad? verilir. Hiperbolün Parametresi Hiperbolün bir oda??nda eksene dik olan kiri? uzunlu?una parametre denir. d?r. Hiperbolün D??merkezli?i oran?na d??merkezlik denir. e > 1 d?r. ,
13. Hiperbolün Asimptotlar? b 2 x 2 - a 2 y 2 = a 2 b 2 hiperbolünün asimptot denklemleri y = d?r. ?kizkenar Hiperbol a = b olan hiperbole ikizkenar hiperbol denir.denklemi x 2 - y 2 = a 2 olur. E?lenik Hiperboller Birinin asal k??eleri , di?erinin yedek k??eleri olan hiperbollere e?lenik hiperboller denir. ile e?lenik hiperbol denklemleridir. ,
14. MERKEZL? KON?KLER?N SINIFLANDIRILMASI Tan?m: R 2 uzay?n?n sabit bir Δ do?rusu ile bunun d???nda sabit bir F noktas? verilsin.F noktas?na olan uzakl???n Δ do?rusuna olan uzakl??a oran? sabit olan P ( x , y ) noktalar?n?n kümesine konik denir.Yani , ( K ) = { P : = e ve e > 0 } d?r. Konik ; e < 1 ise elips , e = 1 ise parabol ve e > 1 ise hiperbol olur. Bu koni?in genel denklemi Ax 2 + B.x.y + Cy 2 +D.x + Ey + F = 0 bi?imindedir. ------------ ---------- P ( x , y ) F ( m , n ) H a.x + b.y + c = 0 , |PF | |PH |
15. Koni?in merkezinin koordinatlar? ; f x = 0 2Ax + B.y + D = 0 f y = 0 B.x + 2C.y + E = 0 Sistemin ??zümü varsa , denklem , merkezli konik (elips,hiperbol) belirtir. δ = | | = 4AC - B 2 = 0 ise merkezli konik vard?r. Δ = diyelim. 1. 4AC - B 2 > 0 ya da B 2 - 4AC < 0 ise konik elips türündendir. a) δ = 4AC - B 2 > 0 ve A . Δ < 0 ise ger?el elips , b) δ > 0 ve A . Δ > 0 ise sanal elips , c) δ > 0 ve Δ = 0 ise nokta elips ( yozla?m?? elips ) olur. Sisteminin ??zümünden elde edilir. , 2A B B 2C A B/2 D/2 B/2 C E/2 D/2 E/2 F
16. 2. 4AC - B 2 < 0 ya da B 2 - 4AC > 0 ise konik hiperbol türündendir. a) δ = 4AC - B 2 < 0 ve Δ = 0 ise denklem hiperbol belirtir. b) δ < 0 ve Δ = 0 ise kesi?en do?ru ?ifti (yozla?m?? hiperbol) belirtir. Genel Konik Denkleminin Parabol Olmas? Durumu δ = 4AC - B 2 = 0 durumunu g?z ?nüne alal?m. i) ise a) D 2 - 4AF > 0 iken parabol bir ?ift paralel do?ru olur. b) D 2 - 4AF = 0 iken parabol ?ak???k iki do?ru olur. c) D 2 - 4AF < 0 ise parabol sanal bir ?ift do?ru g?sterir. i i) ise konik parabol g?sterir. ,
17. GENEL KON?K DENKLEM?N?N STANDART DURUMA D?N??T?R?LMES? Ax 2 + B.x.y + C.y + D.x +E.y +F = 0 denklemi ile verilen genel koni?in fx = 2Ax + B.y + D = 0 fy = B.x + 2C.y + E = 0 x = x ’ + h ve y = y ’ + k konularak x’li ve y’li terimler yok edilir.O zaman genel konik denklemi Ax ’2 + B.x ’ .y ’ + C.y ’2 + F ’ = 0 durumuna girer. x ‘ y ’ lü terimin yok edilebilmesi i?in eksenlerin d?ndürülmesi yap?l?r.Bunun i?in e?itli?ini ger?ekleyen D θ d?nme d?nü?ümü ; sisteminin ??zümünden merkez M(h,k) elde edilir. tan2θ , x ’ cosθ -sinθ x x ’ = x . cosθ - y . sinθ y ’ sinθ cosθ y y ’ = x . sinθ + y . cosθ [ ] = [ ][ ]
18. konularak uygulan?r.Denklem A 1 x 2 + C 1 y 2 + F ’ = 0 bi?imine gelir. A 1 , C 1 katsay?lar?n? θ a??s?na gerek kalmadan a?a??daki gibi bulabilirsiniz. 1) A 1 + C 1 = A + C d?r. 2) A 1 - C 1 = d?r.Karek?k ?nündeki i?aret B’ nin i?areti olarak al?n?r. 3) 4A 1 . C 1 = 4AC - B 2 olur. Bu ü? e?itlikten uygun bi?imde olanlar al?narak A 1 ve C 1 katsay?lar? elde edilir. BA?A D?N
19. ??Z?ML? TEST SORULARI 1. y 2 =4x parabolü i?in a?a??dakilerden hangisi yanl??t?r? A) Oda??n?n koordinatlar? (1, 0) d?r. B) Do?rultman denklemi x= -1 dir. C) (1, -2) noktas?ndaki te?etin denklemi y = -2x-2 dir. E) Tepesi (0, 0) noktas?d?r. CEVAP
20. ??Z?M: A) y 2 = 2px parabolünde odak ( ,0) d?r. 2p = 4 oldu?undan =1 Odak (1,0) olur. B) Do?rultman denklemi x = - = -1 dir. C) ( x 0 ,y 0 ) noktas?ndaki te?et denklemi y y 0 = p( x + x 0 ) dir. (1, -2) noktas?ndaki te?et ise y.(-2) = 2(x+1) den y = -x-1 olur. ( YANLI?) D) Bir do?rultuya paralel kiri?lerin e?leni?i olan ?ap (k??egen) y = dir. Burada y = 2x do?rusunun e?imi 2 dir. ?yleyse ?ap y = =1 olur. E) Tepesi (k??esi) (0,0) noktas?d?r. YANIT : C
21. CEVAP 2. + = 1 elipsi i?in a?a??dakilerden hangisi yanl??t?r? A) Odaklar?n koordinatlar? ( 4,0) d?r. B) D?? merkezli?i e = dir. C) Do?rultmanlar?n?n denklemleri y = dir. D) Parametresi 2p = dür. E) Alan? 15 л dir.
22. ??Z?M : + = 1 elipsinde m ve n den büyük olan? a ve eksen onun üzerindekidir. A) + =1 elipsinde a 2 = 25, b 2 = 9 ve a 2 =b 2 + c 2 den c 2 =16, c = 4 bulunur. Odaklar ( 4, 0) olur. B) D??merkezlik e = = dir. C) Asal eksen x ekseni oldu?undan do?rultmanlar x = x = olur. D) Parametresi 2p = 2 oldu?undan 2p = 2. = elde edilir. E) Alan л ab dir. A = л. 5 . 3 = 15 л olur. YANIT : C
23. CEVAP 3. y = 2px 2 parabollerinden (-1,2) noktas?ndan ge?eni a?a??daki- lerden hangisidir?_ A) y = 8x 2 B) y = 2x 2 C) y = 4x 2 D) y = -4x 2 E) y = -2x 2
24. ??Z?M : Parabol (-1,2) noktas?ndan ge?ece?inden, nokta denklemi sa?lar. 2 = 2p. (-1) 2 p = 1 ve parabol y = 2x 2 olur. YANIT : B
25. CEVAP 4. y 2 = 4x parabolünün ,üzerindeki, (1, -2) noktas?ndan ?izilen te?et denklemi nedir? A) y=x+1 B) y=x-1 C) y=-x-1 D) y=-x+1 E) y=-x+3
26. ??Z?M : y 2 = 2px parabolünün üzerindeki noktas?ndan ?izilen te?et denklemi yy 0 = p(x + x 0 ) idi. ?yleyse (1, -2) noktas?ndaki te?et y.(-2) = 2(x +1) ya da y = - x-1 olur. UYARI : (1,-2) noktas?ndaki te?etin e?imi, m = y` (x ) d?r. 2 y . y` = 4 m = = -1 olur. y - (-2) = -1(x-1) den y = -x-1 elde edilir. YANIT : C
27. CEVAP 5. y = 2x - 1 do?rusunun y = x 2 + kx + k parabolüne te?et olmas? i?in k n?n de?erler kümesi ne olmal?d?r? A) ? B) {- 1,2} C) {8} D) {0,8} E) {0,4}
28. ??Z?M : Do?runun parabole te?et olmas? i?in kesim noktalar?n?n bir tane olmas? gerekir. ?yleyse : 2 x - 1 = x 2 + kx + k dan x 2 + (k - 2) x + k + 1 = 0 denklemi elde edilir. Bu denklem kesim noktalar?n?n apsislerini veren denklemdir. ??züm kümesinin bir elemanl? olmas? i?in Δ = 0 olmal?d?r. Δ = (k -2) 2 - 4(k + 1) = k 2 - 8k elde edilir. Δ = 0 i?in k 2 - 8k = 0 k = 0 vk = 8 Demek ki küme {0,8} dir. YANIT : D
29. CEVAP 6. 4x 2 - 9y 2 = 36 hiperbolüne y = mx do?rusuna paralel iki te?et ?izilebilmesi i?in m ne olmal?d?r? A) B) m = 5 C) m = D) m>0 E) m< - v m>
30. ??Z?M : Hiperbole y = mx do?rusuna paralel ?izilebilecek te?etler asimptotlar? ge?ememelidir. ?yleyse, te?etin e?iminin mutlak de?eri asimptotlar?n e?iminden kü?ük ya da ona e?it olmal?d?r. 4x 2 - 9y 2 =36 ise - =1 ve a 2 =9, b 2 =4 olur. dan elde edilir. YANIT : A
31. CEVAP 7. y 2 =8x parabolünün 0x ekseni ile 135? lik a?? yapan te?eti- nin denklemi nedir? A) y = – x–2 B) y = – x–1 C) y = –x + 2 D) y = –x +1 E) y = x –1
32. ??Z?M : Te?et olacak do?ru y = mx + n olsun. m = tan = tan 135? = – 1 dir. y 2 = 2px parabolüne te?et olma ko?ulu ise p – 2mn = 0 idi. 2p = 8 p = 4 dür. 4– 2. (– 1).n = 0 dan n = – 2 elde edilir. ?yleyse te?et denklemi y = – x– 2 dir. YANIT : A
33. CEVAP 8. 2x 2 + 3y 2 =6 elipsinin d???ndaki P(3, 4) noktas?ndan ?izilen te?etlerinin de?me noktalar?n? birle?tiren kiri?in denklemi nedir? A) x + y =2 B) 2x + y =1 C) x – 2y =1 D) x + 2y =1 E) 2x + 3y =1
34. ??Z?M : + =1 elipsinin d???ndaki P( , ) noktas?ndan ?izilen te?etlerin de?me noktalar?ndan ge?en kiri? denklemi + = 1 dir. Buna g?re: + =1 elipsinde P(3, 4) noktas? i?in kiri? + =1 ya da x+ 2y =1 denklemi olur. YANIT : D
35. CEVAP 9. y 2 = 5x parabolünün hangi kiri?inin orta noktas? M( , –2) dir? A) x + y = – 3 = 0 B) 5x + 4y – 5 = 0 C) 5x + 4y + 13 = 0 D) 4x + 5y – 13 = 0 E) x + 2y – 5 = 0
36. ??Z?M : E?imi m olan kiri?lerinin orta noktalar?n?n kümesi, y = ?ap?d?r. – 2 = den m = bulunur. ?yleyse kiri? denklemi y – y 0 = m(x – x 0 ) dan y – ( – 2) = – (x – ) ya da 5x + 4y – 5 = 0 elde edilir. YANIT : B
37. CEVAP 10. x 2 + 8y = 0 parabolünün dik kesi?en te?etlerinin kesim nokta-lar?n?n kümesi a?a??dakilerden hangisidir? A) y = 2 B) x – 2 = 0 C) y + 2 = 0 D) x =1 E) y = 4
38. ??Z?M : Bir parabolde birbirine dik olan te?etlerin geometrik yeri do?rultmand?r. x 2 = – 8y ve 2p = – 8 dir. ?yleyse geometrik yerin denklemi y = – den y = + 2 olur. YANIT : A
39. CEVAP 11. 4x 2 + 9y 2 – 48x + 72y + 144 = 0 elipsinin merkezi a?a??daki- lerden hangisidir? A) (4, 6) B) (6, 4) C) (3, 4) D) (5, 3) E) (2, 6)
40. ??Z?M : Merkezli koniklerin (elips, hiperbol ) merkezi f x = 0 ve f y = 0 denklemlerinin ortak ??zümünden elde edilir. f x = 8x – 48 = 0 f y = 18y – 72 = 0 sisteminin ??zümünden x = 6, y = 4 elde edilir. UYARI : + = 1 durumuna d?nü?türerek de (h,k) merkezini bulabilirsiniz. YANIT : B TEST?N BA?INA D?N
41. TAMAMLAMALI TEST SORULARI 1. Merkezi elips merkezi ve yar??ap? yar? yedek eksen uzunlu?u olan ?embere .......... ,merkezi elips merkezi ve yar??ap? yar? büyük eksen olan ?embere .......... denir .(elipsin yedek ?emberi,elipsin asal ?emberi) 2. Elipsin bir oda?? merkez ve yar??ap? büyük eksen uzunlu?u olan ?embere .......... denir .(do?rultma ?emberi) 3. Bir elipsin oda??ndan ge?en en k?sa kiri? .......... kiri?tir. (oda?a dik olarak ?izilen) 4. Bir hiperbolün birbirine dik te?etlerinin kesim noktalar?n?n geometrik yeri (monj ?emberinin denklemi) .......... ve odaklar?ndan biri merkez,asal eksen uzunlu?u da yar??ap olan ?embere .......... denir. (x 2 + y 2 = a 2 - b 2 , do?rultman ?emberi ) 5. Bir elipsin yar??ap vekt?rlerinin uzunlu?u .......... ile .......... ve hiperbolün yar??ap vekt?rlerinin uzunluklar? .......... d?r. ( ?le ) 6. Bir ikizkenar hiperbolün odaklar uzunlu?u türünden denklemi .......... ya da x.y= .......... dür. ( )
42. 7. Bir hiperbolde de?i?ken bir te?etle,asimptotlar?n te?kil etti?i ü?genin alan? sabit ve .......... d?r. (a .b ) 8. Bir hiperbolde her te?etin asimptotlar üzerinde ay?rd??? par?alar?n ?arp?m? sabit ve .......... d?r. ( c 2 ) 9. Bir parabolde odaktan ge?en kiri?lerin u?lar?ndaki te?etlerin kesim noktalar?n?n geometrik yeri .......... d?r. ( do?rultman ) 10. Elipsin(ya da hiperbolün) odaklar?n?n herhangi bir te?etine olan uzakl?klar? ?arp?m? sabit ve ........... d?r. ( b 2 )
![GENEL KON?K DENKLEM?N?N STANDART DURUMA D?N??T?R?LMES? Ax 2 + B.x.y + C.y + D.x +E.y +F = 0 denklemi ile verilen genel koni?in fx = 2Ax + B.y + D = 0 fy = B.x + 2C.y + E = 0 x = x ’ + h ve y = y ’ + k konularak x’li ve y’li terimler yok edilir.O zaman genel konik denklemi Ax ’2 + B.x ’ .y ’ + C.y ’2 + F ’ = 0 durumuna girer. x ‘ y ’ lü terimin yok edilebilmesi i?in eksenlerin d?ndürülmesi yap?l?r.Bunun i?in e?itli?ini ger?ekleyen D θ d?nme d?nü?ümü ; sisteminin ??zümünden merkez M(h,k) elde edilir. tan2θ , x ’ cosθ -sinθ x x ’ = x . cosθ - y . sinθ y ’ sinθ cosθ y y ’ = x . sinθ + y . cosθ [ ] = [ ][ ]](https://image.slidesharecdn.com/parabolhiperbolelips-110218153207-phpapp01/85/Parabol-hiperbol-elips-17-320.jpg)
