PPT Hukum Newton
- 1. FISIKA DASAR 1 HUKUM NewTON DISUSUN OLEH; AHMAD FAISAL HARISH 14306144006 MUFIDA DZURIYATIN SYARIFAH 14306144007 SATRIO BAYU PRADHIPTA 14306144009
- 2. FISIKA DASAR 1 HUKUM 1 NEWTON Pada Gerak Lurus Beraturan (GLB) “Setiap benda akan terus dalam keadaan diam, atau akan terus dalam keadaan bergerak rata (uniform) menurut garis lurus, kecuali kalau keadaannya yang demikian itu dipaksa berubah oleh gaya yang bekerja terhadapnya”
- 3. FISIKA DASAR 1 HUKUM 2 NEWTON Pada Gerak Lurus Berubah Beraturan (GLBB) Hukum hanya berlaku untuk sistem dengan massa konstan, variabel massa dapat dikeluarkan dari operator deferensial
- 4. FISIKA DASAR 1 HUKUM 3 NEWTON Newton menggunakan hukum ketiga untuk menurunkan hukum kekekalan momentum ,namun dengan pengamatan yang lebih dalam, kekekalan momentum adalah ide yang lebih mendasar (diturunkan melalui teorema teother dari relativitas Galileo, dibandingkan hukum ketiga, dan tetap berlaku pada kasus yang membuat hukum ketiga newton seakan-akan tidak berlaku. Misalnya ketika medan gaya memiliki momentum, dan dalam mekanika kuantum Dengan, Fa,b adalah gaya- gaya yang berkerja pada A oleh B, dan Fb,a adalah gaya- gaya yang berkerja pada B oleh A
- 5. FISIKA DASAR 1 MOMENTUM Kalau sebuah partikel bermassa m bergerak dengan keceptan (nonrelativistik) dimana massa benda m kostan. Maka, berdasarkan hukum kedua Newton Kalau v1 adalah kecepatan ketika t=t1, dan v2 kecepatan ketika t=t2, maka akibatnya Bentuk integral di ruas kiri dinamakan implus gaya F dalam selang waktu t2-t1 dan merupakan besaran vektor Integral ini tentulah dapat dihitung hanya apabila gaya diketahui sebagai fungsi dari waktu. Akan tetapi bentuk integral di ruas kanan selalu memberikan hasil
- 6. FISIKA DASAR 1 Persamaan yang telah kita turunkan diatas menunjukkan bahwa laju perubahan momentum suatu benda sama dengan gaya total yang bekerja pada benda tersebut selama selang waktu tertentu. ATAU, HUKUM KEKEKALAN MOMENTUM p awal = p akhir
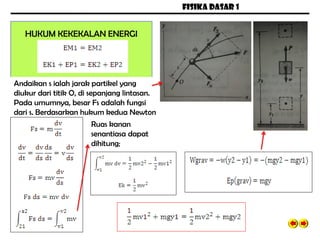
- 7. FISIKA DASAR 1 HUKUM KEKEKALAN ENERGI Andaikan s ialah jarak partikel yang diukur dari titik O, di sepanjang lintasan. Pada umumnya, besar Fs adalah fungsi dari s. Berdasarkan hukum kedua Newton Ruas kanan senantiasa dapat dihitung;
- 8. FISIKA DASAR 1 DAFTAR PUSTAKA Weston Sears, Francis.,W.Zemansky, Mark, Fisika untuk Universitas 1 Mekanika, Panas dan Bunyi. Binacipta, Jakarta, 1962. Vidia, Galih.,Mulyono,Bejo, Olimpiade Fisika SMA Teori Fisika Dasar, Soal-soal, dan Pembahasannya. ANDI, Yogyakarta, 2010. Markus, Setyadi, Maestro Fisika Jilid 1. YRAMA WIDYA, Bandung, 2009.