�ݺ�ߣ

PERSAMAAN LINEAR
• 2 jenis
• 1. Persamaan pada satah
– y=mx +c atau ax +by = c

• 2. Persamaan dalam ruang
– ax + by +cz = d

• Sistem persamaan linear
–
–
–
–
–

Lebih daripada satu persamaan
a1x + b1y = c1 dan a2x + b2y = c2
Atau
a1x + b1y + c1 z = d1 , a2x + b2y + c2 z= d2 ,
a3x + b3y + c3 z = d3

Penyelesaian sistem persamaan
linear

• Dapatkan nilai pembolehubah
• 3 kemungkinan

– Garis bersilang  penyelesaian unik

– Garis bertindih  penyelesaian tidak unik –
lebih daripada satu nilai
– Garis selari  tiada penyelesaian

Penyelesaian sistem persamaan
linear

•

Penyelesaian persamaan linear melibatkan
penyelesaian matriks
tukarkan sistem persamaan linear kpd bentuk matriks

•

 a1 b1   x1   c1 
 a b   x  = c 
 2 2 2  2

a1 x1 + b1 x2 = c1
a2 x1 + b2 x2 = c2
a1 x1 + b1 x 2 + c1 x3 = d1
a 2 x1 + b2 x 2 + c 2 x3 = d 2
a3 x1 + b3 x 2 + c3 x3 = d 3

•

 a1
a
 2
 a3


b1
b2
b3

c1   x1   d1 
c2   x2  =  d 2 
   
c3   x3   d 3 
   

Umumnya btk matriks Ax = B
–

A => matriks pekali , x => vektor penyelesaian dan b =>
vektor lajur

MATRIKS
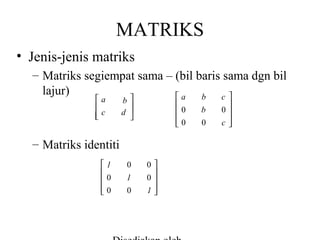
• Jenis-jenis matriks
– Matriks segiempat sama – (bil baris sama dgn bil
lajur)
a
b
c
a


c

b

d 



0
0


– Matriks identiti
1

0
0


0
1
0

0

0
1


b
0


0
c


MATRIKS
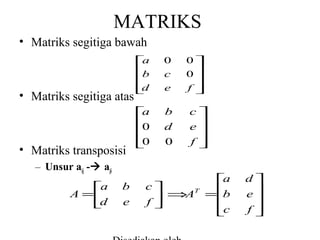
• Matriks segitiga bawah

• Matriks segitiga atas

• Matriks transposisi

a


b


d


0
c
e

a


0


0


b
d
0

0
0

f


c
e

f


– Unsur aij - aji
a
A =
d


b
e

c
⇒ T
A

f

a

=
b

c


d
e

f


MATRIKS
• Matriks simetri  A = AT
1

A = 
2

4


2
1
2

4
2
1


 ⇒ T
A




• Matriks songsangan A-1

1
= 
2


4


2
1
2

4
2
1







– AB = BA = I (matrik identiti)
– A ialah matriks songsangan bagi B dan B ialah
matrik songsangan bagi A
– Disimbolkan A-1 dan B -1
– A-1 A = I

MATRIKS
• Penentu (determinant) |A|
– A=

a


c

b

d 


– |A| = ad – bc

• Sistem persamaan linear mempunyai
penyelesaian unik jika
– Merupakan matriks segiempat sama
– Nilai |A|≠ 0
– Wujud Songsangan matriks A -1

MATRIKS
• Bagaimana menukarkan persamaan linear
ke bentuk matriks imbuhan?
a1 x1 + b1 x2 = c1
a2 x1 + b2 x2 = c2

 a1 b1  x1  c1 

  =  
a2 b2  x2  c2 

• Contoh
2 x1 + 2 x 2 + 1 x3 = 3
-1 x1 + -1 x 2 + 2 x3 = 1
1 x1 + -2 x 2 + 4 x3 = 2

a1 b1 c1 



a2 b2 c 2 

MATRIKS
• Operasi baris permulaan
– Mendarabkan sebarang baris matriks dgn satu
pemalar
– Menambahkan satu persamaan dgn persamaan
lain yang digandakan
– Saling tukarkan baris persamaan matriks

MATRIKS
• Contoh:
• Tukarkan matriks imbuhan berikut ke bentuk
matriks segitiga atas menggunakan operasi baris
permulaan
u11 u12 u13 d1
3 

2
2
1




1 
-1
-1
2

 0 u22 u23 d2 

1
-2
4
2 


 0 0 u33 d3 



MATRIKS

Penyelesaian:
2

 -1
1


2
-1
-2

3 

1
2
4

B3 = B3 + B2



1 
2 


2

 -1
0


2
-1
-3

1
2
6

3 



1 
3 


B2 = B2*2
2

0
0


B2

2
0
-3

1
5
6

3 

B2 = B2+B1


5 
3 


B3
2

0
0


2

1

3 

-3

6

0

5

3 
5 




2

 -2
0


2
-2
-3

1
4
6

3 



2 
3 


MATRIKS
• Bagaimana utk mendapatkan nilai pembolehubah?
2

0
0


2

1

3 

-3

6

0

5

3 
5 




2

0
0


2 x1 + 2 x 2 + 1 x3 = 3
-3 x 2 + 6 x3 = 3
5 x3 = 5
x3 = 1

x2 = 1

x1 = 0

2
-3
0

1 

6
5



 x1
 = 

 x2

 x3

 



3
5

3

Kaedah Penyelesaian Sistem
Persamaan Linear
1. Kaedah Langsung
1.1 Kaedah Penghapusan Gauss
1.2 Kaedah Penghapusan Gauss Jordan
1.3 Kaedah Pemfaktoran Doolittle
1.4 Kaedah Pemfaktoran Crout

2. Kaedah Lelaran (tak langsung)
2.1 Kaedah lelaran Jacobi
2.2 Kaedah Lelaran Gauss-Seidel

�ݺ�ߣ

Spl

Recommended

More Related Content

What's hot (17)

Similar to Spl (6)

More from Muhammad Martayuda (20)

Spl