Ў±ўКЎІЎґўКЎІЎ™ ЎІўДЎ™ЎІЎ≥Ўє
- 1. Ў®Ў≥ўЕ ЎІўДўДўЗ ЎІўДЎ±Ў≠ўЕўЖ ЎІўДЎ±Ў≠ўКўЕ ЎєўЕўД ЎІўДЎЈЎІўДЎ® : Ў®ЎіЎ± ЎµЎІўДЎ≠ Ў®Ў±ўГЎІЎ™ ЎІЎіЎ±ЎІўБ ЎІўДўЕЎєўДўЕ : ўЕЎєўКўЖ Ў®ўЖўК ўЗЎІўЖўК ЎІўДЎєўЖўИЎІўЖ Ў™ўДЎЃўКЎµ ЎѓЎ±ўИЎ≥ ЎІўДўИЎ≠ЎѓЎ© ЎІўДЎЂЎІўЖўКЎ© ЎІўДўЖЎ™ЎІЎђ : Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© ЎІўДЎ™Ў±Ў®ўКЎєўКЎ© Ў®Ў£ўГЎЂЎ± ўЕўЖ ЎЈЎ±ўКўВЎ© Ў™ЎЈЎ®ўКўВ ЎђўЕўКЎє ЎІўДЎЈЎ±ўВ ўИўБўЗўЕ ЎђўЕўКЎє ЎІўДЎЈўДЎІЎ® ўДўЗЎІ ЎІўДЎ™Ў≠ЎІўИЎ± Ў®ўКўЖ ЎІўДЎЈўДЎІЎ® ўИЎІўДўЕЎєўДўЕ ўДЎ≠ўД ЎІўДўЕЎєЎІЎѓўДЎІЎ™
- 2. ЎІўДЎІўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±Ў®ўКЎєўК ўИЎ™ўЕЎЂўКўДўЗ Ў®ўКЎІўЖўКЎІ ўГўЕЎІ Ў™ЎєўДўЕўЖЎІ Ў≥ЎІЎ®ўВЎІ ЎІўЖ ўЕЎєЎІЎѓўДЎ© ЎІўДЎІўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±ўКЎєўК = Ў£Ў≥ ¬≤ + Ў® Ў≥ + ЎђўА Ў≠ўКЎЂ ЎІўЖ Ў£ = ЎµўБЎ±ЎІ ўИўКЎ≥ўЕўЙ ЎђўА ЎІўДЎ≠Ўѓ ЎІўДўЕЎЈўДўВ ўИЎІўДўЕЎђЎІўД ўЗўИ ( Ў≠ ) ўИЎІўДўЕЎѓўЙ ўЕЎђўЕўИЎєЎ© ўВўКўЕ ( Ўµ ) ўЕЎ±ЎІЎђЎєЎ© : Ў£ўК ЎІўДЎІўВЎ™Ў±ЎІўЖЎІЎ™ ЎІўДЎІЎ™ўКЎ© Ў™Ў±Ў®ўКЎєўКЎ© 1) ўВ : ўВ ( Ў≥ ) =2 Ў≥ - Ў≥ ¬≤ 2) Ўє : Ўє ( Ў≥ ) =3-5 Ў≥ 3) ўЗўА : ўЗўА ( Ў≥ ) = Ў≥ ¬≤ + Ў≥ ¬≥ 4) ўД : ўД ( Ў≥ ) =5 Ў≥ ¬≤ ўИЎ≥ўЖЎЈЎ®ўВ ўБўК ўЗЎ∞ЎІ ЎІўДЎѓЎ±Ў≥ ўГўД ўЗЎ∞ЎІ
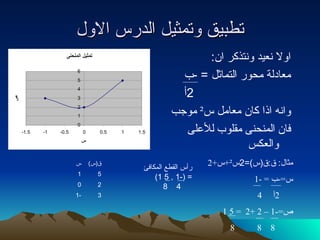
- 3. Ў™ЎЈЎ®ўКўВ ўИЎ™ўЕЎЂўКўД ЎІўДЎѓЎ±Ў≥ ЎІўДЎІўИўД ЎІўИўДЎІ ўЖЎєўКЎѓ ўИўЖЎ™Ў∞ўГЎ± ЎІўЖ : ўЕЎєЎІЎѓўДЎ© ўЕЎ≠ўИЎ± ЎІўДЎ™ўЕЎІЎЂўД = - Ў® 2 Ў£ ўИЎІўЖўЗ ЎІЎ∞ЎІ ўГЎІўЖ ўЕЎєЎІўЕўД Ў≥ ¬≤ ўЕўИЎђЎ® ўБЎІўЖ ЎІўДўЕўЖЎ≠ўЖўЙ ўЕўВўДўИЎ® ўДўДЎ£ЎєўДўЙ ўИЎІўДЎєўГЎ≥ ўЕЎЂЎІўД : ўВ : ўВ ( Ў≥ )=2 Ў≥ ¬≤ + Ў≥ +2 Ў≥ =- Ў® = -1 2 Ў£ 4 Ўµ =-1 вАУ 2 +2 = 5 1 8 8 8 Ў±Ў£Ў≥ ЎІўДўВЎЈЎє ЎІўДўЕўГЎІўБЎ¶ = (-1 , 5 1) 4 8 3 -1 2 0 5 1 ўВ ( Ў≥ ) Ў≥
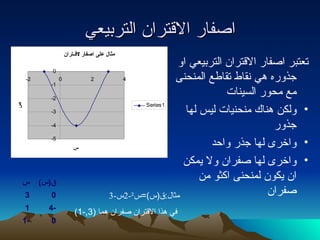
- 4. ЎІЎµўБЎІЎ± ЎІўДЎІўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±Ў®ўКЎєўК Ў™ЎєЎ™Ў®Ў± ЎІЎµўБЎІЎ± ЎІўДЎІўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±Ў®ўКЎєўК ЎІўИ ЎђЎ∞ўИЎ±ўЗ ўЗўК ўЖўВЎІЎЈ Ў™ўВЎІЎЈЎє ЎІўДўЕўЖЎ≠ўЖўЙ ўЕЎє ўЕЎ≠ўИЎ± ЎІўДЎ≥ўКўЖЎІЎ™ ўИўДўГўЖ ўЗўЖЎІўГ ўЕўЖЎ≠ўЖўКЎІЎ™ ўДўКЎ≥ ўДўЗЎІ ЎђЎ∞ўИЎ± ўИЎІЎЃЎ±ўЙ ўДўЗЎІ ЎђЎ∞Ў± ўИЎІЎ≠Ўѓ ўИЎІЎЃЎ±ўЙ ўДўЗЎІ ЎµўБЎ±ЎІўЖ ўИўДЎІ ўКўЕўГўЖ ЎІўЖ ўКўГўИўЖ ўДўЕўЖЎ≠ўЖўЙ ЎІўГЎЂўИ ўЕўЖ ЎµўБЎ±ЎІўЖ ўЕЎЂЎІўД : ўВ ( Ў≥ )= Ў≥ ¬≤ -2 Ў≥ -3 ўБўК ўЗЎ∞ЎІ ЎІўДЎІўВЎ™Ў±ЎІўЖ ЎµўБЎ±ЎІўЖ ўЗўЕЎІ (3,-1) 0 -1 -4 1 0 3 ўВ ( Ў≥ ) Ў≥
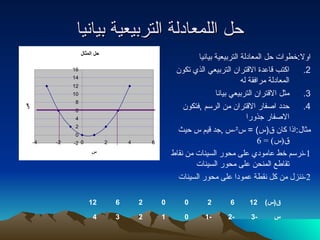
- 5. Ў≠ўД ЎІўДўДўЕЎєЎІЎѓўДЎ© ЎІўДЎ™Ў±Ў®ўКЎєўКЎ© Ў®ўКЎІўЖўКЎІ ЎІўИўДЎІ : ЎЃЎЈўИЎІЎ™ Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© ЎІўДЎ™Ў±Ў®ўКЎєўКЎ© Ў®ўКЎІўЖўКЎІ ЎІўГЎ™Ў® ўВЎІЎєЎѓЎ© ЎІўДЎІўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±Ў®ўКЎєўК ЎІўДЎ∞ўК Ў™ўГўИўЖ ЎІўДўЕЎєЎІЎѓўДЎ© ўЕЎ±ЎІўБўВЎ© ўДўЗ ўЕЎЂўД ЎІўДЎІўВЎ™Ў±ЎІўЖ ЎІўДЎ™Ў±Ў®ўКЎєўК Ў®ўКЎІўЖЎІ Ў≠ЎѓЎѓ ЎІЎµўБЎІЎ± ЎІўДЎІўВЎ™Ў±ЎІўЖ ўЕўЖ ЎІўДЎ±Ў≥ўЕ , ўБЎ™ўГўИўЖ ЎІўДЎІЎµўБЎІЎ± ЎђЎ∞ўИЎ±ЎІ ўЕЎЂЎІўД : ЎІЎ∞ЎІ ўГЎІўЖ ўВ ( Ў≥ ) = Ў≥ ¬≤ - Ў≥ , ЎђЎѓ ўВўКўЕ Ў≥ Ў≠ўКЎЂ ўВ ( Ў≥ ) = 6 1- ўЖЎ±Ў≥ўЕ ЎЃЎЈ ЎєЎІўЕўИЎѓўК ЎєўДўЙ ўЕЎ≠ўИЎ± ЎІўДЎ≥ўКўЖЎІЎ™ ўЕўЖ ўЖўВЎІЎЈ Ў™ўВЎІЎЈЎє ЎІўДўЕўЖЎ≠ўЖ ЎєўДўЙ ўЕЎ≠ўИЎ± ЎІўДЎ≥ўКўЖЎІЎ™ 2- ўЖўЖЎ≤ўД ўЕўЖ ўГўД ўЖўВЎЈЎ© ЎєўЕўИЎѓЎІ ЎєўДўЙ ўЕЎ≠ўИЎ± ЎІўДЎ≥ўКўЖЎІЎ™ Ў≥ -3 -2 -1 0 1 2 3 4 ўВ ( Ў≥ ) 12 6 2 0 0 2 6 12
- 6. Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© ЎІўДЎ™Ў±Ў®ЎєўКЎ© Ў®ЎЈЎ±ўКўВЎ© ЎІўДЎ™Ў≠ўДўКўД ЎІўДўЙ ЎІўДЎєўИЎІўЕўД ўЕЎєўДўИўЕЎ© ЎІЎ∞ЎІ ўГЎІўЖ Ў£ , Ў® ЎєЎѓЎѓўКўЖ Ў≠ўВўКўВўКўКўЖ ўИ ўГЎІўЖ Ў£ * Ў® =0 ўБЎІўЖ Ў£ =0 ЎІўИ Ў® =0 ЎІўИ ўГўДЎІўЗўЕЎІ = 0 ўДЎ≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© ЎІўДЎ™Ў±Ў®ўКЎєўКЎ© Ў≠ўД ЎІўДЎЈЎ±ўБ ЎІўДЎІўКўЕўЖ ўЕўЖ ЎІўДўЕЎєЎІЎѓўДЎ© ЎІЎ≥Ў™ЎЃЎѓўЕ ЎІўДўЕЎєўДўИўЕЎ© ўБўК ЎІўДЎІЎєўДўЙ ўДўДЎ≠ЎµўИўД ЎєўДўЙ ўЕЎєЎІЎѓўДЎ™ўКўЖ ЎЃЎЈўКЎ™ўКўЖ Ў≠ўД ўГўД ўЕўЖ ЎІўДўЕЎєЎІЎѓўДЎ™ўКўЖ ўИ ( ЎђЎѓ ўВўКўЕ Ў≥ ) ўИўДЎ≠ЎЄ ЎІўЖ ўВўКўЕ Ў≥ Ў™Ў≠ўВўВ ЎІўДўЕЎєЎІЎѓўДЎ© ЎІўДЎ™ўК Ў™Ў≠ўД ЎєўДўКўЗЎІ
- 7. ўЕЎЂЎІўД : ўКЎ≤ўКЎѓ ўЕЎЂўДЎІ ЎєЎ±Ўґ ўЕЎ≥Ў™ЎЈўКўД ЎєўЖ ЎЈўИўДўЗ Ў®ўЕўВЎѓЎІЎ± 6 Ў≥ўЕ , ЎІЎ∞ЎІ ЎєўДўЕЎ™ ЎІўЖ ўЕЎ≥ЎІЎ≠Ў™ўЗ 56 Ў≥ўЕ ¬≤ . ЎђЎѓ ўГўДЎІ ўЕўЖ ЎЈўИўДўЗ ўИЎєЎ±ЎґўЗ ЎІўДЎ≠ўД : ўЖўБЎ±Ўґ ЎІўЖ ЎІўДЎєЎ±Ўґ = Ў≥ ўБўЕЎЂўДЎІўЗ = 2 Ў≥ ўЖўБЎ±Ўґ ЎІўЖ ЎІўДЎЈўИўД = Ўµ ўБўКўГўИўЖ 2 Ў≥ -6 ЎІЎ∞ўЖ 56= Ў≥ (2 Ў≥ -6) Ў£ўК ЎІўЖ Ў≥ ¬≤ -6 Ў≥ -56=0 ўИЎ®ЎґЎ±Ў® ЎЈЎ±ўБўК ЎІўДўЕЎєЎІЎѓўДЎ© ўБўК 1 ўЖЎ≠ЎµўД ЎєўДўЙ Ў≥ ¬≤ -3 Ў≥ -28=0 ўИЎ®ЎІўДЎ™Ў≠ўДўКўД Ў™Ў≠ЎµўД ЎєўДўЙ : ( Ў≥ -7) ( Ў≥ +4)=0 ўЖЎ≥Ў™ўЖЎ™Ўђ ўЕўЖ ( Ў≥ -7)=0 ЎІўЖ Ў≥ =7 ўИўЕўЖ ( Ў≥ +4)=0 ЎІўЖ Ў≥ =-4 Ў™ўЗўЕўД ўДЎІўЖўЗ ўЕўЖ ЎІўДўЕЎ≥Ў™Ў≠ўКўД ЎІўЖ Ў™ўГўИўЖ ЎІЎЈўИЎІўД ўЕЎ≥Ў™ЎЈўКўД = Ў≥ЎІўДЎ®ЎІ ЎІЎ∞ўЖ ўКўГўИўЖ ЎІўДЎєЎ±Ўґ =7 Ў≥ўЕ , ўИ ЎІўДЎЈўИўД =7*2-6 = 14-6 =8 Ў≥ўЕ
- 8. Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© ЎІўДЎ™Ў±Ў®ўКЎєўКЎ© Ў®ЎІЎ≥Ў™ЎЃЎѓЎІўЕ ЎІўГўЕЎІўД ЎІўДўЕЎ±Ў®Ўє Ў™ўЕўЗўКЎѓ : ЎІўКўЕўЕЎІ ўКЎ£Ў™ўК ўЕЎ±Ў®ЎєЎІЎ™ ўГЎІўЕўДЎ© 1) Ў≥ ¬≤ -4 Ў≥ +4 2) Ў≥ ¬≤ -6 Ў≥ -9 3)4 Ў≥ ¬≤ +32 Ў≥ +64 ўЕЎєўДўИўЕЎ© : ЎІЎ∞ЎІ ўГЎІўЖ Ў≥ ¬≤ = Ў£ Ў≠ўКЎЂ Ў£ЎєЎѓЎѓ Ў≠ўВўКўВўК ўЕўИЎђЎ® ўБЎІўЖ Ў≥ = + Ў£ ўКЎ±ўЕЎ≤ ўДўДўЕЎђўЕўИЎєЎ© ЎІўДЎЃЎІўДўКЎ© Ў®Ў±ўЕЎ≤ O Ў£ўИ {} ЎІўДЎЃЎЈўИЎІЎ™ :1- ЎђЎєўД ўЕЎєЎІўЕўД Ў≥ ¬≤ =1 2- ўГЎ™ЎІЎ®Ў© ўЕЎєЎІўЕўДЎІ ЎІўДўЕЎєЎІЎѓўДЎ© 3- ўЖўВўД ЎІўДЎ≠Ўѓ ЎІўДЎЂЎІЎ®Ў™ ЎІўДўЙ ЎІўДЎЈЎ±ўБ ЎІўДЎІЎЃЎ± 4- ЎІЎґЎІўБЎ© ( ўЕЎєЎІўЕўД Ў≥ ) ¬≤ ЎІўДўЙ ЎЈЎ±ўБўК ЎІўДўЕЎєЎІЎѓўДЎ© 2 5- Ў™Ў≠ўДўКўД ЎІўДЎЈЎ±ўБ ЎІўДЎІўКўЕўЖ ўИўГЎ™ЎІЎ®Ў™ўЗ Ў®ЎµўИЎ±Ў© ўЕЎ±Ў®Ўє ўГЎІўЕўД 6- Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© ЎІўДўЖЎІЎ™ЎђЎ©
- 9. ўЕЎЂЎІўД : ЎІЎ≥Ў™ЎЃЎѓўЕ ЎЈЎ±ўКўВЎ© ЎІўГўЕЎІўД ЎІўДўЕЎ±Ў®Ўє ўБўК Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© Ў≥ ¬≤ -2 Ў≥ +4=0 ЎІўДЎ≠ўД : ўЖўВўД ЎІўДЎ≠Ўѓ ЎІўДЎЂЎІЎ®Ў™ ЎІўДўЙ ЎІўДЎЈЎ±ўБ ЎІўДЎІЎЃЎ± : Ў≥ ¬≤ _2 Ў≥ =-4 Ў® =-2 ЎІЎ∞ўЖ ,(-2) ¬≤ = (-1) ¬≤ =1 2 ўЖЎґўКўБўЗ ЎІўДўЙ ЎІўДЎЈЎ±ўБўКўЖ ўБўКЎµЎ®Ў≠ Ў≥ ¬≤ -2 Ў≥ +1=-4+1 Ў≥ ¬≤ -2 Ў≥ +1=-3 ўИўЕўЖўЗ ( Ў≥ -1) ¬≤ =-3 ўИЎ®ўЗЎ∞ЎІ ўЖЎ≥Ў™ўЖЎ™Ўђ ЎІўЖўЗ ўДЎІўКўЕўГўЖ ўИЎђўИЎѓ Ў≠ўДўИўД Ў≠ўВўКўВўКЎ© ўДўДўЕЎєЎІЎѓўДЎ© ўИЎєўДўКўЗ ўБЎІўЖ ўЕЎђўЕўИЎєўЗ ЎІўДЎ≠ўД = {}
- 10. Ў≠ўД ЎІўДўЕЎєЎІЎѓўДЎ© ( Ў≥ +3) ¬≤ =9 ЎІўДЎ≠ўД : Ў≥ +3=+ 3 ўИўЕўЖўЗ Ў≥ +3 = +3 Ў£ўК Ў≥ =0 ЎІўИ Ў≥ +3=-3, Ў£ўК Ў≥ =-6 Ў™ўЕ Ў®Ў≠ўЕЎѓ ЎІўДўДўЗ ЎєўЕўД ЎІўДўИЎ≠Ўі: Ў®ЎіЎ± Ў®Ў±ўГЎ™Ў© ЎІЎіЎ±ЎІўБ ЎІўДўЕЎєўДўЕ ЎІўДўБЎІЎґўД Ў£.ўЕЎєўКўЖ Ў®ўЖўК ўЗЎІўЖўК