การแปลงทาง�รྺาคณิต
- 1. รายวิชา หน่วยการเรียนรู้ที่ 4 ใบความรู้ท่ี 1 คณิตศาสตร์ การแปลงทาง�รྺาคณิต (ค 22101) ระดับชั้น มัธยมศึกษาปีที่ 2 การเล่ ือนขนาน การเลื่อนขนานบนระนาบเป็นการแปลงทาง�รྺาคณิตที่มีการเลื่อนจุด ทุกจุดไปบนระนาบตามแนวเส้นตรงในทิศทางเดียวกันและเป็นระยะทาง ที่เท่ากันตามที่กำาหนด ตัวอย่าง กำาหนดให้ ABC เป็นรูปต้นแบบ เมื่อเลื่อนขนาน ABC ไปในทิศทางและระยะทางตามที่กำาหนดดังรูป แล้วแ A′B ′C ′ เป็น ภาพที่ได้จากการเลื่อนขนาน A L S B P B′ P′ C C′ จากรูป จะเห็นว่า มีการเลื่อนจุด A ไปที่จุด A′ เลื่อนจุด B ไปที่จุด B′ และ เลื่อนจุด C ไปที่จุด C′ ในทิศทางเดียวกันและเป็นระยะเท่า กัน จะได้ว่า A′A′ , B ′B ′ และ C ′C ′ ขนานกันและยาวเท่ากัน 1
- 2. ถ้า P เป็นจุดใด ๆ บน ABC แล้วจะมี P′ บน A′B ′C ′ เป็น จุดที่สมนัยกันกับจุด P และ PP ′ จะขนานและยาวเท่ากันกับความยาว ของ AA′ , BB ′ และ CC ′ ด้วย ในการบอกทิศทางและระยทางของการเลื่อนขนาน จะได้เวก เตอร์ เป็นตัวกำาหนด จากตัวอย่างข้างต้นอาจใช้เวกเตอร์ MN เพื่อบอกทิศทางและระยะทาง A A′ ของการเลื่อนขนานดังรูป B P B′ P′ C C′ M N เวกเตอร์ MN อาจเขียนแทนด้วย MN ซึ่ง จะมีทิศทางจากจุด เริ่มต้น M ไปยังจุดสิ้นสุด N และมีขนาดเท่ากับความยาวของ จากตัวอย่างการเลื่อนขนานข้างต้นจะได้ว่า 1. A′ A′ , B ′B ′ , C ′C ′ และ P ′P ′ จะขนานกันกับ MN MN 2. AA′ = BB ′ = CC ′ = PP ′ จะขนานกันกับ MN การกำาหนดเวกเตอร์ของการเลื่อนขนานอาจให้จุดเริ่มต้นอยู่บนรูป ต้นแบบหรืออยู่นอกรูปต้นแบบก็ได้ ในการเลื่อนขนาน เมือกำาหนดเวกเตอร์ของการเลื่อนขนานรูป ่ ต้นแบบมาให้ เราต้องวิเคราะห์ว่าจะต้องเลื่อนรูปต้นแบบไปในทิศทาง ใด และเป็นระยะเท่าไร ถ้าเวกเตอร์ของการเลื่อนขนานที่กำาหนดให้ขนานกับแกน X หรือ แกน Y การเลื่อนขนานรูปต้นแบบก็จะกระทำาได้ง่าย แต่ถ้าเวกเตอร์ที่ 2
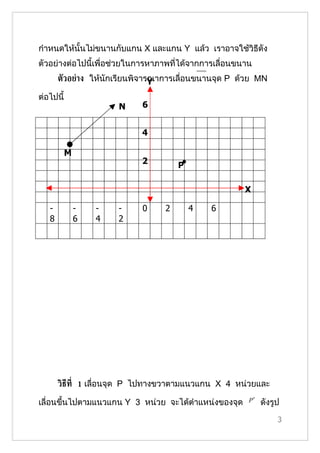
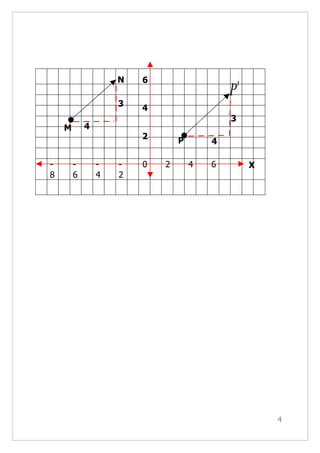
- 3. กำาหนดให้นั้นไม่ขนานกับแกน X และแกน Y แล้ว เราอาจใช้วิธีดัง ตัวอย่างต่อไปนี้เพื่อช่วยในการหาภาพที่ได้จากการเลื่อนขนาน ตัวอย่าง ให้นักเรียนพิจารณาการเลื่อนขนานจุด P ด้วย MN Y ต่อไปนี้ N 6 4 M 2 P• X - - - - 0 2 4 6 8 6 4 2 วิธีท่ี 1 เลื่อนจุด P ไปทางขวาตามแนวแกน X 4 หน่วยและ เลื่อนขึ้นไปตามแนวแกน Y 3 หน่วย จะได้ตำาแหน่งของจุด P′ ดังรูป 3
- 4. N 6 P′ 3 4 3 M 4 2 P 4 - - - - 0 2 4 6 X 8 6 4 2 4
- 5. รายวิชา หน่วยการเรียนรู้ที่ 4 แบบฝึ กพัฒนาการเรียน คณิตศาสตร์ การแปลงทาง�รྺาคณิต รูท่ี 1 ้ (ค 22101) ระดับชั้น มัธยมศึกษาปีที่ 2 การเล่ ือนขนาน กำำหนด DEF จงเขียนภำพทีได้จำกกำรเลื่อนขนำน ่ DEF ด้วย MN Y D M 6 4 F 2 N E - - - 0 2 4 X 6 6 4 2 5
- 6. ร้ปแบบการประ�มิน ดี พอใชู ควร ปรับปรุง ประเมินตนเอง ประเมินผลจากครู ประเมินผลจากผู้ปกครอง ชื่อ.......................................................................................ชั้น.... .............เลขที.............. ่ รายวิชา หน่วยการเรียนรู้ที่ 4 แบบทดสอบก่อนเรียน- คณิตศาสตร์ การแปลงทาง�รྺาคณิต หลังเรียนท่ี 1 (ค 22101) ระดับชั้น มัธยมศึกษาปีที่ 2 การเล่ ือนขนาน 1. จงหาพิกัึϾ�องจุด (3,-1) ที่เกิดจากการเลื่อนขนานเดียวกับการส่ง จุด B (-2,6) ไปยังจุด (6,2) ก. (11,-5) ข. (13-4) ค. (5,-5) ง. (0,-11) 2. จงหาพิกัึϾ�องจุด A (4,-2) ที่เกิดจากการเลื่อนขนานเดียวกันการ ส่งจุด B (-1,5) ไปยังจุด B′ (5,1) 6
- 7. ก. (0,-8) ข. (2,-2) ค. (10,-6) ง. (8,4) 3. ข้อใดจัดเป็นการเลื่อนขนาน ก. เข็มนาฬิกาที่กำาลังเดิน ข. เงาของต้นไม้ในลำาธาร ค. รถไฟที่แล่นตรงไป ง. ชิงช้าสวรรค์ 4. เลื่อนจุด (5,7) ไปทางซ้าย 6 หน่วย จะเป็นจุดใด ก. (5,13) ข. (11,7) ค. (-1,7) ง. (-5,1) 5. เลื่อนจุด (-8,3) ไปทางซ้าย 4 หน่วย จะเป็นจุดใด ก. (-8,7) ข. (-4,3) ค. (-12,3) ง. (-8,-1) ชื่อ.......................................................................................ชั้น.... .............เลขที.............. ่ รายวิชา หน่วยการเรียนรู้ที่ 4 ใบความรู้ท่ี 2 คณิตศาสตร์ การแปลงทาง�รྺาคณิต 7
- 8. (ค 22101) ระดับชั้น มัธยมศึกษาปีที่ 2 การสะทูอน การสะท้อนบนระนาบเป็นการแปลงทาง�รྺาคณิตที่มีเส้นตรง ที่ ตรึงเส้นหนึ่งเป็นเส้นสะท้อน แต่ละจุด P บนระนาบจะมีจุด P′ เป็นภาพ ที่ได้จากการสะท้อนจุด P โดยที่ 1. ถ้าจุด P ไม่อยู่บนเส้นตรง แล้วเส้นตรง จะแบ่งครึ่งและตั้งฉาก กับ PP ′ 2. ถ้าจุด P อยู่บนเส้นตรง แล้วจุด P และจุด P ′ เป็นจุดเดียวกัน ตัวอย่างการสะท้อนที่มีเส้นตรง เป็นเส้นสะท้อน A C C′ B B′ A′ รูปเรขาคณิตที่สามารถหารอยพับและพับรูปทั้งสองข้างของรอย พับให้ทับกันสนิทได้เรียกว่า รูปสมมาตรบนเส้น และเรียกรอยพับนั้นว่า D C P แกนสมมาตร รูปสมมาตรบนเส้นแต่ละรูปอาจมีจำานวนแกนสมมาตรไม่ เท่ากัน เช่น E F A Q B 8
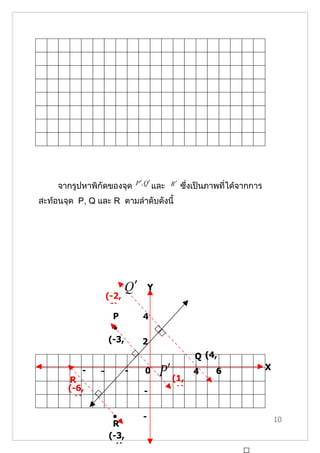
- 9. ABCD เป็นรูปสี่เหลี่ยมจัตุรัสและเป็นรูปสมมาตรบนเส้นที่มี แกนสมมาตร 4 เส้นได้แก่ AC , BD , EF และ PQ รูปสมมาตรบนเส้นเป็นรูปที่เกิดจากการสะท้อน โดยมีแกน สมมาตรเป็นเส้นสะท้อน ในกรณีที่กำาหนดเส้นสะท้อนเป็นเส้นตรงที่ไม่ใช่แกน X หรือแกน Y อาจหาพิกันของจุดที่เป็นภาพที่ได้จากการสะท้อนจุดที่กำาหนดให้ โดยพิจารณาดังนี้ ถ้าเส้นสะท้อนไม่ขนานกับแกน X และไม่ขนานกับแกน Y แต่ เป็นเส้นในแนวทแยง ให้ลากเส้นตรงผ่านจุดที่กำาหนดให้และตั้งฉากกับ เส้นสะท้อน ภาพของจุดที่กำาหนดให้จะอยู่บนเส้นตั้งฉากที่สร้างขึ้น และอยู่ห่างจากเส้นสะท้อนเป็นระยะเท่ากันกับที่จุดที่กำาหนดให้อยู่ห่าง Y จากเส้นสะท้อน เมื่อได้ภาพของจุดนั้นแล้วจึงหาพิกัด ตัวอย่าง กำาหนดจุด P( -٣,٣), Q(٤,٠) และ R (-٤-,٣) มีเส้นตรง P 4 ผ่านจุด (-٢- ,٤) และ (١,٣) ดังรูป • (1, • (-3, 2 3) -3) Q (4, • 0) X - - - 0 2 4 6 6 4 2 • (-4, - -2) 2 9 • - R 4 (-3,
- 10. P ′, Q ′ R′ จากรูปหาพิกัึϾ�องจุด และ ซึ่งเป็นภาพที่ได้จากการ สะท้อนจุด P, Q และ R ตามลำาดับดังนี้ Q′ Y (-2, 6) P 4 • (-3, 2 -3) Q (4, R 6 - - 4 - 2 0 P ′ (1, 4 0) 6 X (-6, - -1) -1) 2 • - 10 R 4 (-3, -4)
- 11. ١) ลากเส้นตรง m ١ ผ่านจุด P และให้ตั้งฉากกับเส้นสะท้อน ٢) หาจุด P′ บนเส้นตรง m ١ ที่ทำาให้จุด P และจุด P′ อยู่ห่าง จากเส้นตรง เท่ากัน ٣) จากรูป จะได้พิกัึϾ�องจุด P ′ เป็น (١-,١) ٤) ในทำานองเดียวกัน เมื่อลากเส้นตรง m ٢ ผ่านจุด Q และให้ Q′ Q′ ตั้งฉากกับเส้นสะท้อน แล้วหาจุด จะได้พิกัึϾ�องจุด เป็น (-٢,٦) ٥) ในทำานองเดียวกันเมื่อลากเส้นตรง m ٣ ผ่านจุด R และให้ตั้ง ฉากกับเส้นสะท้อน แล้วหาจุด R′ จะได้พิกัึϾ�องจุด R′ เป็น (-١- ,٦) 11
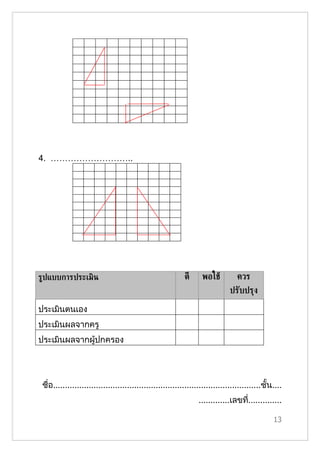
- 12. รายวิชา หน่วยการเรียนรู้ที่ 4 แบบฝึ กพัฒนาการเรียน คณิตศาสตร์ การแปลงทาง�รྺาคณิต รูท่ี 2 ้ (ค ٢٢١٠١) ระดับชั้น มัธยมศึกษาปีที่ ٢ การสะทูอน ให้นักเรียนพิจารณาว่าข้อใดเป็นรูปสะท้อน และข้อใดเป็นรูปการเลื่อน ขนาน 1. ……………………….. 2. ………………………. 3. ………………………. 12
- 13. 4. ……………………….. ร้ปแบบการประ�มิน ดี พอใชู ควร ปรับปรุง ประเมินตนเอง ประเมินผลจากครู ประเมินผลจากผู้ปกครอง ชื่อ.......................................................................................ชั้น.... .............เลขที.............. ่ 13
- 14. รายวิชา หน่วยการเรียนรู้ที่ 4 แบบทดสอบก่อนเรียน- คณิตศาสตร์ การแปลงทาง�รྺาคณิต หลังเรียนท่ี 2 (ค 22101) ระดับชั้น มัธยมศึกษาปีที่ 2 การสะทูอน ให้นักเรียนทำาเครื่องหมายกากบาท (X) ลงหน้าข้อที่เป็นคำาตอบถูก 1. ข้อใดจัดเป็นการสะท้อน ก. เงาของต้นไม้ในลำาธาร 14
- 15. ข. เข็มนาฬิกาที่กำาลังเดิน ค. ชิงช้าสวรรค์ ง. รถไฟที่แล่นตรงไป 2. ถ้ารูปต้นแบบคือ แล้วภาพของ A′ ที่เกิดจากการสะท้อนโดยมี แกน X เป็นเส้นสะท้อน คือข้อใด ก. ข. ค. ง. 3. กำาหนด AB โดยมีแกน X เป็นเส้นสะท้อน จุด A มีพิกัดเป็น (-3,4) และจุด B มีพิกัดเป็น (4,-2) จงหาพิกัึϾ�องจุด A′ และ B ′ ก. A′ (-3,-4), B ′ (4,2) ข. A′ (-3,4), B ′ (-4,2) ค. A′ (3,4), B ′ (-4,-2) ง. A′ (3,-4), B ′ (-4,2) 4 .ถ้ารูปหนึ่งเกิดจากการแปลงอีกรูปหนึ่ง โดยที่จุด P แปลงไปเป็นจุด Y จุด Q แปลงไปเป็นจุด X และจุด R แปลงไปเป็นจุด Z ดังรูป 15
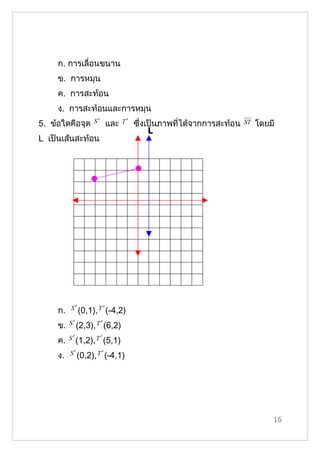
- 16. ก. การเลื่อนขนาน ข. การหมุน ค. การสะท้อน ง. การสะท้อนและการหมุน 5. ข้อใดคือจุด S′ และ T′ ซึ่งเป็นภาพที่ได้จากการสะท้อน ST โดยมี L L เป็นเส้นสะท้อน S ก. S ′ (0,1), T ′ (-4,2) ข. S ′ (2,3), T ′ (6,2) ค. S ′ (1,2), T ′ (5,1) ง. S ′ (0,2), T ′ (-4,1) 16
- 17. ชื่อ.......................................................................................ชั้น.... .............เลขที.............. ่ รายวิชา หน่วยการเรียนรู้ที่ 4 ใบความรู้ท่ี 3 คณิตศาสตร์ การแปลงทาง�รྺาคณิต (ค 22101) ระดับชั้น มัธยมศึกษาปีที่ 2 การหมุน การหมุนบนระนาบเป็นการแปลงทาง�รྺาคณิตที่มีจุด O ที่ตรึงจุดหนึ่ง เป็นจุดหมุนแต่ละจุด P บนระนาบ มีจด ุ P′ เป็นภาพที่ได้จากการหมุน จุด P รอบจุด O ตามทิศทางที่กำาหนดด้วยมุมที่มีขนาด k โดยที่ 1) ถ้าจุด P ไม่ใช่จุด O แล้ว OP = OP ′ และขนานของ ˆ POP ′ เท่ากับ k 2) ถ้าจุด P เป็นจุดเดียวกันกับ O แล้ว P เป็นจุดหมุน ตัวอย่าง จุดหมุน O อยู่บนรูปต้นแบบ 1) 17
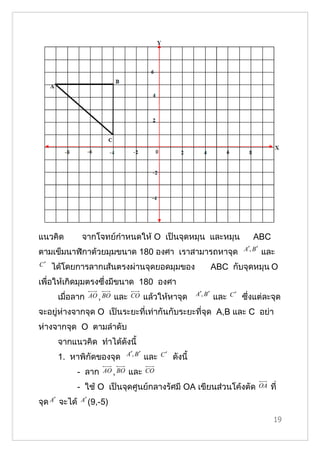
- 18. ตัวอย่างที่ 1 ถ้า A′B ′C ′ เป็นภาพที่ได้จากการหมุน ABC ที่ กำาหนดให้ รอบจุดกำาเนิด O ตามเข็มนาฬิกาด้วยมุมขนาด 180 องศา จงหา A′, B ′ C′ 1) พิกัึϾ�องจุด และ ซึ่งเป็นภาพที่ได้จากการหมุนจุด A,B และ C ตามลำาดับ 2) ∆ A′B ′C ′ ซึ่งเป็นภาพที่ได้จากการหมุน ABC 18
- 19. แนวคิด จากโจทย์กำาหนดให้ O เป็นจุดหมุน และหมุน ABC A′, B ′ ตามเข็มนาฬิกาด้วยมุมขนาด 180 องศา เราสามารถหาจุด และ C′ ได้โดยการลากเส้นตรงผ่านจุดยอดมุมของ ABC กับจุดหมุน O เพื่อให้เกิดมุมตรงซึ่งมีขนาด 180 องศา A′, B ′ C′ เมื่อลาก AO , BO และ CO แล้วให้หาจุด และ ซึ่งแต่ละจุด จะอยู่ห่างจากจุด O เป็นระยะที่เท่ากันกับระยะที่จุด A,B และ C อย่า ห่างจากจุด O ตามลำาดับ จากแนวคิด ทำาได้ดังนี้ A′, B ′ C′ 1. หาพิกัึϾ�องจุด และ ดังนี้ - ลาก AO , BO และ CO - ใช้ O เป็นจุดศูนย์กลางรัศมี OA เขียนส่วนโค้งตัด OA ที่ จุด A′ จะได้ A′ (9,-5) 19
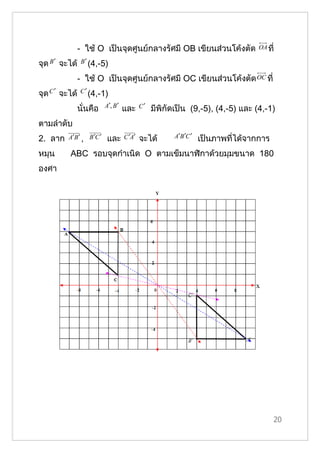
- 20. - ใช้ O เป็นจุดศูนย์กลางรัศมี OB เขียนส่วนโค้งตัด OA ที่ จุด B ′ จะได้ B ′ (4,-5) - ใช้ O เป็นจุดศูนย์กลางรัศมี OC เขียนส่วนโค้งตัด OC ที่ จุด C ′ จะได้ C ′ (4,-1) A′, B ′ C′ นั่นคือ และ มีพิกัดเป็น (9,-5), (4,-5) และ (4,-1) ตามลำาดับ 2. ลาก A′B ′ , B ′C ′ และ C ′A′ จะได้ A′B ′C ′ เป็นภาพที่ได้จากการ หมุน ABC รอบจุดกำาเนิด O ตามเข็มนาฬิกาด้วยมุมขนาด 180 องศา 20
- 21. รายวิชา หน่วยการเรียนรู้ที่ 4 แบบฝึ กพัฒนาการเรียน คณิตศาสตร์ การแปลงทาง�รྺาคณิต รูท่ี 3 ้ (ค 22101) ระดับชั้น มัธยมศึกษาปีที่ 2 การหมุน P ′Q ′R ′S ′ : เป็นภาพที่ได้จาการหมุน PQRS ทวนเข็มนาฬิกา ด้วยมุมที่มีขนาด 90 องศา 21
- 22. พิกัึϾ�องจุด P′ = (.....................) Q′ พิกัึϾ�องจุด = (.....................) พิกัึϾ�องจุด R′ = (.....................) พิกัึϾ�องจุด S′ = (.....................) ร้ปแบบการประ�มิน ดี พอใชู ควร ปรับปรุง ประเมินตนเอง ประเมินผลจากครู ประเมินผลจากผู้ปกครอง ชื่อ.......................................................................................ชั้น.... .............เลขที.............. ่ รายวิชา หน่วยการเรียนรู้ที่ 4 แบบทดสอบก่อนเรียน- คณิตศาสตร์ การแปลงทาง�รྺาคณิต หลังเรียนท่ี 3 (ค 22101) ระดับชั้น 22
- 23. มัธยมศึกษาปีที่ 2 การหมุน 1. ข้อใดคือภาพที่เกิดจากการหมุน รอบ จากรูปที่กำาหนดให้ 90° ทวนเข็มนาฬิกา ก. ข. ค. ง. 2. รูปสามเหลี่ยม ABC จุด A มีพิกัดเป็น (3,0) จุด B มีพิกัดเป็น (5,1) และจุด C มีพิกัดเป็น (2,3) จงหาพิกัึϾ�องจุด C บนภาพจากการหมุน รูปสามเหลี่ยม ABC โดยหมุนรอบจุดกำาเนิดด้วยมุม 180° ก. (2,3) ข. (2,-3) ค. (-2,3) ง. (-2,-3) 3. รูปสามเหลี่ยม DEF จุด D มีพิกัดเป็น (3,0) จุด E มีพิกัดเป็น (5,1) และ จุด F มีพิกัดเป็น (2,3) จงหาพิกัึϾ�องจุด E บนภาพจากการหมุน รูปสามเหลี่ยม DEF โดยหมุนรอบจุดกำาเนิดด้วย 180° ก. (5,-1)) ข. (-5,-1) ค. (5,1) ง. (-5,1) 23
- 24. 4. ข้อใดเป็นการหมุน ABC โดยการหมุนเข็มนาฬิกา และมีจุด P เป็นจุดหมุน เป็นมุม 90 องศา ก. ข. ค. ง. 5. ข้อใดจัดเป็นการหมุน ก. เงาของต้นไม้ในลำาธาร ข. เข็มนาฬิกาที่กำาลังเดิน ค. ชิงช้าสวรรค์ ง. รถไฟที่แล่นตรงไป ชื่อ.......................................................................................ชั้น.... .............เลขที.............. ่ 24
- 25. 25