トーナメントは运か実力か
?
0 likes?1,980 views
第７回日曜数学会の発表スライドです。 https://www.facebook.com/events/858311494303516/ 発表の様子はこちら http://www.nicovideo.jp/watch/sm29957704
トーナメントは运か実力か
- 2. 自己紹介 ? 福原和朗 @kazurof ? twitter, Qiita, github などやってます。 ? 所属 ? GMO リサーチ ? アンケートシステムの開発保守 2
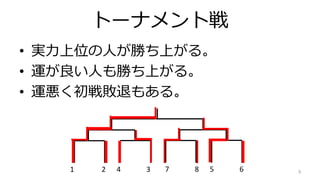
- 3. トーナメント戦 ? 実力上位の人が勝ち上がる。 ? 運が良い人も勝ち上がる。 ? 運悪く初戦敗退もある。 31 2 4 3 7 8 5 6
- 5. 前提条件 ? 参加者 2n (n = 1, 2, 3, … ) 人のトーナメ ントを考える。 ? 2, 4, 8, 16, … ? n 回勝ったら優勝という意味。 ? 各参加者は番号で区別 ? 1, 2, 3, … ? 試合結果は番号が小さいほうが勝つ。 ? それぞれの試合に運要素無し。 ? 右側左側は区別しない。 5 1 2
- 6. 手順 ? 調べ方 1. 全てのトーナメント組み合わせを列挙 2. トーナメント実行 3. 結果の順位の分布をとる ? 出したい結果 ? a 人中実力 b 位の人が c 回戦を勝つ確率 d % 6
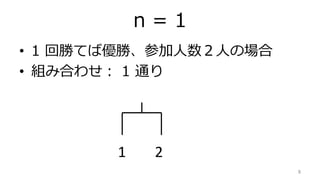
- 8. n = 1 ? 1 回勝てば優勝、参加人数２人の場合 ? 組み合わせ： 1 通り 8 1 2
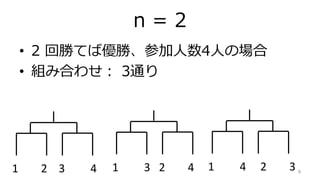
- 9. n = 2 ? 2 回勝てば優勝、参加人数4人の場合 ? 組み合わせ： 3通り 91 2 3 4 1 3 2 4 1 4 2 3
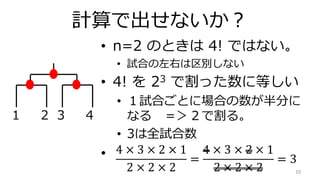
- 10. 計算で出せないか？ ? n=2 のときは 4! ではない。 ? 試合の左右は区別しない ? 4! を 23 で割った数に等しい ? １試合ごとに場合の数が半分に なる ＝＞２で割る。 ? 3は全試合数 ? 10 1 2 3 4 4 × 3 × 2 × 1 2 × 2 × 2 = 4 × 3 × 2 × 1 2 × 2 × 2 = 3
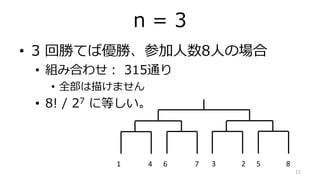
- 11. n = 3 ? 3 回勝てば優勝、参加人数8人の場合 ? 組み合わせ： 315通り ? 全部は描けません ? 8! / 27 に等しい。 11 1 4 6 7 3 2 5 8
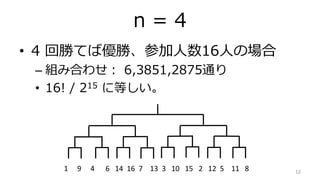
- 12. n = 4 ? 4 回勝てば優勝、参加人数16人の場合 – 組み合わせ： 6,3851,2875通り ? 16! / 215 に等しい。 121 9 4 6 14 16 7 13 3 10 15 2 12 5 11 8
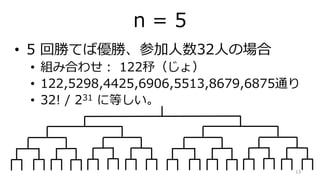
- 13. n = 5 ? 5 回勝てば優勝、参加人数32人の場合 ? 組み合わせ： 122?（じょ） ? 122,5298,4425,6906,5513,8679,6875通り ? 32! / 231 に等しい。 13
- 14. 一般項はこうだ！（未証明） ? 一般項 ? 漸化式 ? 割り算しないのでプログラムでも安心 14 ?(?)= (2 ?)! 2(2 ? ?1) ? 1 = 1 ? ? = 2 ? ? 1 ? × ?(? ? 1)
- 15. どんな結果になった？ 15 n = 4 の場合（5の場合なんて無理です orz）
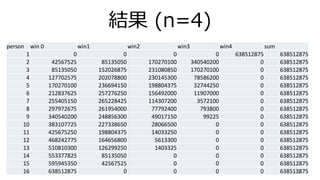
- 16. 結果 (n=4) person win 0 win1 win2 win3 win4 sum 1 0 0 0 0 638512875 638512875 2 42567525 85135050 170270100 340540200 0 638512875 3 85135050 152026875 231080850 170270100 0 638512875 4 127702575 202078800 230145300 78586200 0 638512875 5 170270100 236694150 198804375 32744250 0 638512875 6 212837625 257276250 156492000 11907000 0 638512875 7 255405150 265228425 114307200 3572100 0 638512875 8 297972675 261954000 77792400 793800 0 638512875 9 340540200 248856300 49017150 99225 0 638512875 10 383107725 227338650 28066500 0 0 638512875 11 425675250 198804375 14033250 0 0 638512875 12 468242775 164656800 5613300 0 0 638512875 13 510810300 126299250 1403325 0 0 638512875 14 553377825 85135050 0 0 0 638512875 15 595945350 42567525 0 0 0 638512875 16 638512875 0 0 0 0 63851287516
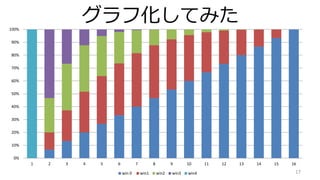
- 17. グラフ化してみた 17 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 win 0 win1 win2 win3 win4
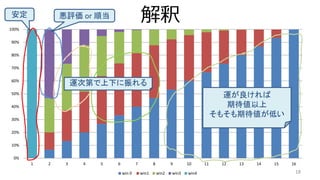
- 18. 解釈 18 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 win 0 win1 win2 win3 win4 運が良ければ 期待値以上 そもそも期待値が低い 運次第で上下に振れる 悪評価 or 順当安定
- 21. 一般化 ? もっと統計を取って調べたいが… ? n = 5 だと122 ?（じょ） ? 122,5298,4425,6906,5513,8679,6875通り ? n = 4, (16人)が現実的な計算の限界。 ? すごい計算機なら、 n = 5 ぐらいはできる？ 21
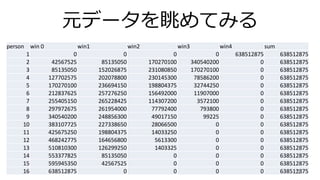
- 22. 元データを眺めてみる person win 0 win1 win2 win3 win4 sum 1 0 0 0 0 638512875 638512875 2 42567525 85135050 170270100 340540200 0 638512875 3 85135050 152026875 231080850 170270100 0 638512875 4 127702575 202078800 230145300 78586200 0 638512875 5 170270100 236694150 198804375 32744250 0 638512875 6 212837625 257276250 156492000 11907000 0 638512875 7 255405150 265228425 114307200 3572100 0 638512875 8 297972675 261954000 77792400 793800 0 638512875 9 340540200 248856300 49017150 99225 0 638512875 10 383107725 227338650 28066500 0 0 638512875 11 425675250 198804375 14033250 0 0 638512875 12 468242775 164656800 5613300 0 0 638512875 13 510810300 126299250 1403325 0 0 638512875 14 553377825 85135050 0 0 0 638512875 15 595945350 42567525 0 0 0 638512875 16 638512875 0 0 0 0 63851287522
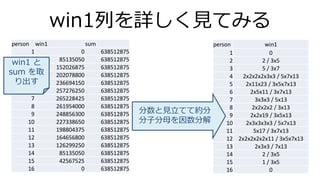
- 23. win1列を詳しく見てみる 23 person win1 1 0 2 2 / 3x5 3 5 / 3x7 4 2x2x2x2x3x3 / 5x7x13 5 2x11x23 / 3x5x7x13 6 2x5x11 / 3x7x13 7 3x3x3 / 5x13 8 2x2x2x2 / 3x13 9 2x2x19 / 3x5x13 10 2x3x3x3x3 / 5x7x13 11 5x17 / 3x7x13 12 2x2x2x2x2x11 / 3x5x7x13 13 2x3x3 / 7x13 14 2 / 3x5 15 1 / 3x5 16 0 person win1 sum 1 0 638512875 2 85135050 638512875 3 152026875 638512875 4 202078800 638512875 5 236694150 638512875 6 257276250 638512875 7 265228425 638512875 8 261954000 638512875 9 248856300 638512875 10 227338650 638512875 11 198804375 638512875 12 164656800 638512875 13 126299250 638512875 14 85135050 638512875 15 42567525 638512875 16 0 638512875 分数と見立てて約分 分子分母を因数分解 win1 と sum を取 り出す
- 24. win1列を詳しく (2) 24 person win1 比 1 0 2 2 / 3x5 2x7 / 5x5 3 5 / 3x7 5x5x13 / 2x2x2x2x3x3x3 4 2x2x2x2x3x3 / 5x7x13 2x2x2x3x3x3 /11x 23 5 2x11x23 / 3x5x7x13 23 / 5x5 6 2x5x11 / 3x7x13 2x5x11x5 / 3x3x3x3x7 7 3x3x3 / 5x13 3x3x3x3 / 2x2x2x2x5 8 2x2x2x2 / 3x13 2x2x5 / 19 9 2x2x19 / 3x5x13 2x19x7 / 3x3x3x3x3 10 2x3x3x3x3 / 5x7x13 2x3x3x3x3x3 / 5x5x17 11 5x17 / 3x7x13 5x5x17 / 2x2x2x2x2x11 12 2x2x2x2x2x11 / 3x5x7x13 2x2x2x2x11 / 3x3x3x5 13 2x3x3 / 7x13 3x3x3x5 / 7x13 14 2 / 3x5 2 15 1 / 3x5 16 0 上段の数と下段の数の 比を計算してみた。
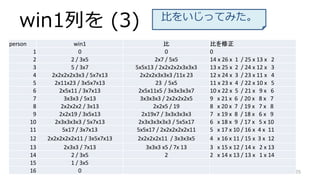
- 25. win1列を (3) 25 person win1 比 比を修正 1 0 0 0 2 2 / 3x5 2x7 / 5x5 14 x 26 x 1 / 25 x 13 x 2 3 5 / 3x7 5x5x13 / 2x2x2x2x3x3x3 13 x 25 x 2 / 24 x 12 x 3 4 2x2x2x2x3x3 / 5x7x13 2x2x2x3x3x3 /11x 23 12 x 24 x 3 / 23 x 11 x 4 5 2x11x23 / 3x5x7x13 23 / 5x5 11 x 23 x 4 / 22 x 10 x 5 6 2x5x11 / 3x7x13 2x5x11x5 / 3x3x3x3x7 10 x 22 x 5 / 21 x 9 x 6 7 3x3x3 / 5x13 3x3x3x3 / 2x2x2x2x5 9 x 21 x 6 / 20 x 8 x 7 8 2x2x2x2 / 3x13 2x2x5 / 19 8 x 20 x 7 / 19 x 7 x 8 9 2x2x19 / 3x5x13 2x19x7 / 3x3x3x3x3 7 x 19 x 8 / 18 x 6 x 9 10 2x3x3x3x3 / 5x7x13 2x3x3x3x3x3 / 5x5x17 6 x 18 x 9 / 17 x 5 x 10 11 5x17 / 3x7x13 5x5x17 / 2x2x2x2x2x11 5 x 17 x 10 / 16 x 4 x 11 12 2x2x2x2x2x11 / 3x5x7x13 2x2x2x2x11 / 3x3x3x5 4 x 16 x 11 / 15 x 3 x 12 13 2x3x3 / 7x13 3x3x3 x5 / 7x 13 3 x 15 x 12 / 14 x 2 x 13 14 2 / 3x5 2 2 x 14 x 13 / 13 x 1 x 14 15 1 / 3x5 16 0 比をいじってみた。
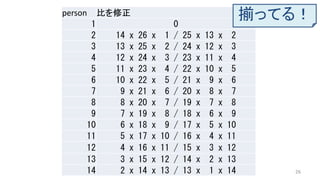
- 26. 26 person 比を修正 1 0 2 14 x 26 x 1 / 25 x 13 x 2 3 13 x 25 x 2 / 24 x 12 x 3 4 12 x 24 x 3 / 23 x 11 x 4 5 11 x 23 x 4 / 22 x 10 x 5 6 10 x 22 x 5 / 21 x 9 x 6 7 9 x 21 x 6 / 20 x 8 x 7 8 8 x 20 x 7 / 19 x 7 x 8 9 7 x 19 x 8 / 18 x 6 x 9 10 6 x 18 x 9 / 17 x 5 x 10 11 5 x 17 x 10 / 16 x 4 x 11 12 4 x 16 x 11 / 15 x 3 x 12 13 3 x 15 x 12 / 14 x 2 x 13 14 2 x 14 x 13 / 13 x 1 x 14 揃ってる！
- 27. この調子で一般化できる？ 27
- 29. まとめ ? 16人トーナメントで調べてみた。 ? 実力下位の人はラッキーなら期待値以上 ? 実力上位の人は運要素で上下に振れる ? ２位の人は運ゲー。 ? １位の人が全部持っていく。 ? 勝数分布には規則性ありそう ? 類題知ってる人おしえて！ 29
- 31. トーナメントは运か実力か 福原和朗 (@kazurof ) 第7回 日曜数学会 2016-10-01 31 ご清聴ありがとうございました