More Related Content
What's hot (20)
PDF
Introduction of introduction_to_group_theoryshima o?
Similar to mathemaical_notation (20)
PDF
¢|Š®Č╝╩ą┤¾č¦ źŪ®`ź┐ĮŌ╬÷╚ļķT 6 ╗žÄóĘų╬÷ż╚źŌźŪźļ▀xÆk 1hirokazutanaka?
More from Kenta Oono (20)
PDF
Minimax statistical learning with Wasserstein distances (NeurIPS2018 Reading ...Kenta Oono?
PDF
Deep learning for molecules, introduction to chainer chemistryKenta Oono?
PDF
Overview of Machine Learning for Molecules and Materials Workshop @ NIPS2017Kenta Oono?
PDF
Comparison of deep learning frameworks from a viewpoint of double backpropaga...Kenta Oono?
PDF
╔Ņ▓Ń覎░źšźņ®`źÓź’®`ź»Ė┼ꬿ╚░õ│¾▓╣Š▒▓į▒░∙ż╬╩┬└²╔▄ĮķKenta Oono?
PDF
GTC Japan 2016 Chainer feature introductionKenta Oono?
PDF
Common Design of Deep Learning FrameworksKenta Oono?
PDF
2015─Ļ9į┬18╚š (GTC Japan 2015) ╔Ņīėč¦┴Ģźšźņ®`źÓź’®`ź»Chainerż╬ī¦╚ļż╚╗»║Ž╬’╗ŅąįėĶ£yżžż╬ÅĻė├ Kenta Oono?
PDF
Introduction to Chainer (LL Ring Recursive)Kenta Oono?
PDF
╚š▒Š╔±ĮU╗ž┬Ęč¦╗ßź╗ź▀ź╩®`ĪĖČ┘▒▒▒Ķ│ó▒▓╣░∙▓įŠ▒▓į▓Ąż“╩╣ż├żŲż▀żĶż”ŻĪĪ╣ū╩┴ŽKenta Oono?
mathemaical_notation
- 2. Ė┼ę¬
? ─┐Ą─
? ╩²č¦ėø║┼Ż¼╩²č¦╣½╩Įż“╦╝żż│÷ż╣
? ūŅ│§ż╬ę╗ÜiżŪż─ż▐ż║ż½ż╩żż
? ─┌╚▌
? ╩²č¦ėø║┼
? ╣½╩ĮŻ©ųĖ╩²?īØ╩²Ż¼╬óĘų?ĘeĘųŻ®
? Ų½╬óĘųŻ©??”żŻ®
? ąą┴ą
- 4. ź«źĻźĘźŃ╬─ūų
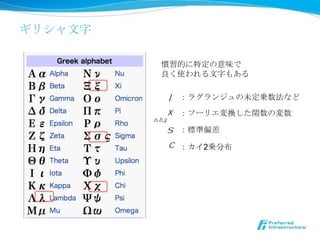
æT┴ĢĄ─ż╦╠žČ©ż╬ęŌ╬ČżŪ
┴╝ż»╩╣ż’żņżļ╬─ūųżŌżóżļ
l Ż║źķź░źķź¾źĖźÕż╬╬┤Č©ü\╩²Ę©ż╩ż╔
x Ż║źš®`źĻź©ēõōQżĘż┐ķv╩²ż╬ēõ╩²
a, b, g
s Ż║ś╦£╩Ų½▓Ņ
c Ż║ź½źż2ü\Ęų▓╝
- 5. ╣╠ėą├¹į~ż╚żĘżŲ╩╣ż’żņżļėø║┼
? NŻ║ūį╚╗╩²╚½╠Õ = {0, 1, 2, ĪŁ} Ż©0ż“║¼żÓż½żŽ┴„┼╔ż╦żĶżļŻ®
? ZŻ║š¹╩²╚½╠Õ = {ĪŁ, -2, -1, 0, 1, 2, ĪŁ}
? RŻ║īg╩²╚½╠Õ
? CŻ║č}╦ž╩²╚½╠Õ
? Ż© QŻ║ėą└Ē╩²╚½╠ÕŻ®
? n ? N => ĪĖnżŽūį╚╗╩²żŪż╣Ī╣
? x ? Z => ĪĖxżŽš¹╩²żŪżŽżóżĻż▐ż╗ż¾Ī╣
- 6. ╝»║Žż╦īØż╣żļėø║┼
? Ī╩Ż©╝»║Žż╦╩¶ż╣żļŻ®ż╚ ?Ż©▓┐Ęų╝»║ŽżŪżóżļŻ®ż╬▀`żżż╦ūóęŌ
? x Ī╩ AŻ║xżŽ╝»║ŽAż╬į¬żŪżóżļ
? 1 Ī╩ {1, 2, 3}, {3, 4, 5} Ī╩ { {1, 2}, {3, 4, 5}, {6, 7} }
? B ? AŻ║BżŽAż╬▓┐Ęų╝»║ŽżŪżóżļ
? {1, 2} ? {1, 2, 3}, { {3, 4, 5} } ? { {1, 2}, {3, 4, 5}, {6, 7} }
N?Z?Q?R?C
? ╝»║Žż¼Ą╚żĘżżł÷║Žż“║¼żßżļż½żŽ┴„┼╔ż¼żóżļ
(1) (2) (3)
šµ▓┐Ęų╝»║Ž A?B A?B A?B
▓┐Ęų╝»║Ž A?B A?B A?B
- 7. ╝»║Žż╬ėøĘ©
? ┤¾ļj░čż╦2═©żĻż╬ėøĘ©ż¼żóżļ
? 1. į¬ż“╚½żŲĢ°żŁż»ż└ż╣
S = {1, 3, 5, 7, 9}
? 2. į¬ż╬£║ż┐ż╣╠§╝■ż“Æżż▓żļ
S = {x ? N | x % 2 =1, x ?10}
S = {x | x ? N, x is odd and is less than or equal to 10}
? źĻź╣ź╚ż╬─┌░³▒Ēėøż╦īØÅĻż╣żļ
? HaskellŻ║
? PythonŻ║
- 9. ųĖ╩²Ż¼īØ╩²ķv▀B╣½╩Į
? Č©┴x
? a, bż“š²ż╬īg╩²ż╚żĘżŲ a x = b ? x = loga b
? ūį╚╗īØ╩²ż╬ĄūŻ║ e = 2.728?
? loge x ż“ log xżõ ż╚Ģ°ż»╩┬żŌ
ln x
? ╣½╩Į
? šµ╩²ż╬ż½ż▒╦Ń log(x Ī┴ y) = log x + log y
? ╠žż╦Ż¼ log x n = n log x
? šµ╩²ż╬ĖŅżĻ╦Ń log(x / y) = log x - log y
? ųĖ╩²Ę©ät
e(x+y) = e x Ī┴ e y
- 10. ╬óĘųŻ¼╗²Ęųķv┴¼╣½╩Į
d n
? ČÓĒŚ╩Įż╬╬óĘų (x n )? = (x ) = nx n-1
dx
? Ęeż╬╬óĘųż╬╣½╩Į ( f Ī┴ g)? = f ? Ī┴ g + f Ī┴ g?
? ║Ž│╔ķv╩²ż╬╬óĘų ( f (g(x)))? = f ?(g(x))Ī┴ g?(x)
? ╣½╩ĮżĮż╬żŌż╬żĶżĻ╩╣żżĘĮż“┴ĢĄ├żĘżŲż»ż└żĄżż
? └²Ż║ d ?d ? ?d ? 1 3
(log x 3 )? = ? logt Ī┬ Ī┴ ? x 3 Ī┬ = Ī┴ (3x 2 ) =
dx ©© dt ? ©© dx ? t x
Ī³
t=x3ż╚ż¬żżżŲ║Ž│╔ķv╩²ż╬╬óĘų
f(t)=log t, g(x)=x3
©░
? ČÓĒŚ╩Įż╬ĘeĘų 1 n+1
x n dx = x + C (n ? -1) Ī¹ n=?1żŪżŽĘų─Ėż¼0ż╦ż╩żļ
n +1
©░x -1
dx = log x + C
- 12. ČÓēõ╩²ż“▒Ēż╣ėø║┼
? 1éĆż╬īg╩²ż“▒Ēż╣ėø║┼żŽ╝ÜūųŻ¼č}╩²ż╬īg╩²ż╬ĮMż“▒Ēż╣ėø║┼żŽ╠½ūųż“ė├żż
żļ╩┬ż¼ČÓżż
? └²Ż║ x = ( x1, x2 , x3, x4 )
f (x) = x 3
g(x) = x1 + x2 + x3 + x4
h(x) = (x, x 2 + x, x 3 - x)
? ęįĮĄżŌż│ż╬ėøĘ©ż╦ÅŠż├żŲżżżŁż▐ż╣
? Č©┴xė“Ż¼éÄė“ż“├„╩Šż╣żļż│ż╚żŪżŌĘųż½żĻżõż╣ż»ż╩żĻż▐ż╣
? ╔Žż╬└²ż╬ł÷║Ž f :R?R
g : R4 ? R
h : R ? R3
- 13. Ų½╬óĘųŻ©Č©┴xŻ®
? ČÓēõ╩²ķv╩²Ż©ēõ╩²ż¼2ż─ęį╔Žż╬ķv╩²Ż®żŪ1ż─ęį═Ōż╬ż╣ż┘żŲż╬ēõ╩²ż“Č©╩²
ż└ż╚╦╝ż├żŲ╬óĘųż╣żļ▓┘ū„
? └²Ż║ f (x, y, z) = x 3 + y 2 + z 5
?f ?f
(x, y, z) = fx (x, y, z) = 3x 2 (x, y, z) = f y (x, y, z) = 2y
?x ?y
?f
(x, y, z) = fz (x, y, z) = 5z 4
?z
- 14. Ų½╬óĘų═¼╩┐ż╬ķvéS
? f ż¼╩«Ęų╗¼żķż½Ż©= x, yż╦ż─żżżŲ║╬╗žżŪżŌ╬óĘų┐╔─▄Ż®ż╩żķżą
fxy (x, y, z) = fyx (x, y, z)
Ī³ Ī³
ż▐ż║xżŪ╬óĘųżĘ ż▐ż║yżŪ╬óĘųżĘ
żŪżŁż┐ķv╩²ż“żĄżķż╦yżŪ╬óĘųż╣żļ żŪżŁż┐ķv╩²ż“żĄżķż╦xżŪ╬óĘųż╣żļ
? ż│żņż“└RżĻĘĄżĘė├żżżļż╚Ż¼
fxyzyyxwzxxzy (x, y, z) = fxxxxxyyyyzzzw (x, y, z)
Ī· Ų½╬óĘųż╣żļĒśą“żŽ║├żŁż╩żĶż”ż╦øQżßżŲżĶżż
- 15. ?Ż©ź╩źųźķŻ®
? ČÓēõ╩²ķv╩²ż╬1ļAŲ½╬óĘųż“üKż┘żŲŻ¼ź┘ź»ź╚źļż╦ż╣żļ▓┘ū„
? └²Ż║ f (x, y, z) = x 3 + y 2 + z 5
?f (x, y, z) = (3x 2 , 2y, 5z 4 ) Ż©ąąź┘ź»ź╚źļż╬ł÷║ŽŻ®
? ?
? 3x 2 Ī┬
?f (x, y, z) = ? 2y Ī┬ Ż©┴ąź┘ź»ź╚źļż╬ł÷║ŽŻ®
? Ī┬
©© 5z 4 ?
? ┴ą/ąąź┘ź»ź╚źļż╔ż┴żķżŪė├żżżļż½żŽ╬─├}/╣Pš▀ż╦żĶżļ
? (x, y, z)ż“ż▐ż╚żßżŲ xż╚Ģ°żżżŲŻ¼Ī²ż╬żĶż”ż╦Ģ°ż»╩┬żŌżóżļ
?f
(x) = (3x 2 , 2y, 5z 4 )
?x
- 16. ”żŻ©źķźūźķźĘźóź¾Ż®
? ČÓēõ╩²ķv╩²ż╬2ļAŲ½╬óĘųż“ż╣ż┘żŲūŃżĘ║Žż’ż╗ż┐żŌż╬
?2 ?2 ?2
Df (x, y, z) = 2 f + 2 f + 2 f f : R3 ? Rż╩żķ
?x ?y ?z
? ?2 ?f żŽź┘ź»ź╚źļ
?2 ?2 ?
=? 2 + 2 + 2 Ī┬ f Df
©© ?x ?y ?z ? żŽź╣ź½źķ®`Ż©īg╩²Ż®
= f xx + f yy + fzz .
? └²Ż║ f (x, y, z) = x 3 + y 2 + z 5 ż╬ż╚żŁŻ¼
?2 ?2 ?2
f = 6x f =2 f = 20z 3 ż└ż½żķŻ¼
?x 2 ?y 2 ?z 2
Df (x, y, z) = 20z 3 + 6x + 2.
- 18. ąą┴ąż╬▒ĒżĘĘĮ
? ╩²ūųż“ķLĘĮą╬╔Žż╦üKż┘ż┐żŌż╬
? ąą┴ążŽ┤¾╬─ūųźóźļźšźĪź┘ź├ź╚żŪ▒Ēż╣╩┬ż¼ČÓżż
? ║ßż¼ąąŻ¼┐kż¼┴ąŻ©ż█ż╚ż¾ż╔Įyę╗żĄżņżŲżżżļŻ®
? n ąą m ┴ąż╬ąą┴ąż“ nĪ┴m ąą┴ąż╚┬įż╣żļż│ż╚żŌŻ©ąąż¼Ž╚Ż®
? A = (aij )ż╚Ģ°żżż┐żķŻ¼i ąą j ┴ą─┐ż¼aijŻ©żõż├żčżĻąąż¼Ž╚Ż®
┴ąŻ©columnŻ®
? a11 a12 ? a1m ?
? Ī┬ ąąŻ©rowŻ®
? a21 a22 ? a1m Ī┬
? Ī┬
? ? ? ? ? Ī┬
? an1 an2 ? anm Ī┬
©© ?
- 19. ąą┴ąż╬Ęe
? AŻ║pĪ┴q ąą┴ąŻ¼BŻ║źĄźżź║ qĪ┴r ąą┴ą
? Aż╬┴ąż╚Bż╬ąąż¼ę╗ų┬żĘżŲżżżļż╚żŁABżŽČ©┴x┐╔─▄
? ABżŽ pĪ┴r ąą┴ą
? BAżŽČ©┴xżŪżŁżļż╚żŽŽ▐żķż╩żż
? ąą┴ąż╬Ęeż╬│╔Ęų▒Ē╩Š
qĪ┴
? A = (aij ), B = (bijż╚ż¬ż»ż╚Ż¼ABż╬ i ąą j │╔ĘųżŽ
) ?a ik Ī┴ bkj
k=1
- 20. ąą┴ąż╬▓┘ū„Ż©ąą┴ą╩ĮŻ®
? ąą┴ą╩Į (determinant)Ż║ det A =| A |
? └²ż©żą─µąą┴ąż¼┤µį┌ż╣żļż½ż╬┼ąČ©ż╦ė├żżżļ
? └²Ż║ Ż©š²ĘĮąą┴ąż╦żĘż½detżŽČ©┴xżŪżŁż╩żżż│ż╚ż╦ūóęŌŻ®
? a b ?
? A=? Ī┬ ż╩żķ det A = ad - bc
©© c d ?
? ?
? a b c Ī┬
? A=? d e f Ī┬ ż╩żķ det A = aei + bfg + cdh - afh - bdi - ceg
? g h i Ī┬
©© ?
? ąą┴ąnĪ┴nż╬ąą┴ąA, Bż╦īØżĘżŲ
det AB = det AĪ┴ det B
- 21. ąą┴ąż╬▓┘ū„Ż©▄×ų├Ż®
? ▄×ų├Ż©transposeŻ®Ż║ At = AT = t A = T A
? ż╔żņżŌ═¼żĖęŌ╬ČŻ¼ż│ż│żŪżŽūŅ│§ż╬ėø║┼ż“╩╣żżż▐ż╣
? ąąż╚┴ąż“╚ļżņ╠µż©żļ▓┘ū„
? Aż╬ i ąą j ┴ą─┐ż╚Aż╬ j ąą i ┴ą─┐żŽĄ╚żĘżż
? └²Ż║ ? 1 ?
? Ī┬
? A = (1 2 3)ż╬ż╚żŁŻ¼ A t = ? 2 Ī┬
? 3 Ī┬
©© ?
? a b ?
? Ī┬ ? a c e ?
? A = ? c d Ī┬ ż╬ż╚żŁŻ¼ A t = ? Ī┬
? e f Ī┬ ? b d f Ī┬
©© ? ©© ?
- 22. ąą┴ąż╬─┌ĘeŻ©ą╬ż└ż▒Ż®
? ąą┴ąż╬ż½ż▒╦Ńż╬└²Ż║
? x, yŻ║nĪ┴1ż╬┴ąź┘ź»ź╚źļ, AŻ║nĪ┴nąą┴ąż╬ż╚żŁ
x t Ay
żŽż┐ż└ż╬īg╩²
? š²Č©éÄŻ©Į±╗žżŽšh├„╩Ī┬įŻ®ż╬nĪ┴nąą┴ąAż¼żóżļż╚Ż¼żĮż│ż½żķ2ż─ż╬ź┘ź»
ź╚źļż╬Ż©Aż½żķøQż▐żļŻ®ķgż╬─┌Ęe < x, y >ż“Ż© x Ī┴ y ż╚żŌĢ°ż»Ż®
< x, y >= xt Ay
ż╚Č©┴xżŪżŁżļ