![ランダム幾何学的複体 Betti 数の変化
Figure: [0, 1]4
内の 1000 点から計算した Betti 数の変化
観察
? β0 は単調減少. b1 は単調ではない.
? β0 ? 1, β1 は r が大きくなると 0 になる.
? s.t.@simizut22 14](https://image.slidesharecdn.com/16simizut-210923135912/85/16-simizut-14-320.jpg)
![漸近挙動と相転移 β0
Theorem ([Penrose et al., 2003])
1. nrd
n → 0 の亞臨界域において,
E[β0,n] ≈ n (n → ∞)
2. nrd
n → λ ∈ (0, 1) の臨界域において,
? 大数の法則が成立: 0 < c < 1 が存在して,
β0,n ≈ cn (n → ∞)
? 中心極限定理が成立:
β0,n ? E[β0,n]
√
n
d
?
→ N(0, ?
σ2
)
3. nrd
n = 2d?1
dωd
(c + log n) の時,
P(β0,n = 1) → e?e?c
? s.t.@simizut22 19](https://image.slidesharecdn.com/16simizut-210923135912/85/16-simizut-19-320.jpg)
![漸近挙動と相転移 亞臨界域
Theorem ([Kahle and Meckes, 2013])
limn→∞ nrd
n → 0 の亞臨界域において, 次の極限が存在:（大数の法則）
E[β1,n]
n4r3d
n
→ C1.
Theorem ([Kahle and Meckes, 2013] )
1. n4
r3d
n → 0 の時,
P(β1,n = 0) → 1
2. n4
r3d
n → α ∈ (0, ∞) の時,
β1,n
d
?
→ Poisson(C1α).
3. n4
r3d
n → ∞ の時, 次の中心極限定理が成立:
β1,n ? E[β1,n]
Var(β1,n)
d
?
→ N(0, 1).
? s.t.@simizut22 20](https://image.slidesharecdn.com/16simizut-210923135912/85/16-simizut-20-320.jpg)
![漸近挙動と相転移 臨界域
Theorem ([Kahle and Meckes, 2013])
limn→∞ nrd
n → c の臨界域(critical regime)において,
β1,n ～ n (n → ∞).
? s.t.@simizut22 21](https://image.slidesharecdn.com/16simizut-210923135912/85/16-simizut-21-320.jpg)
![漸近挙動と相転移 超臨界域
Theorem ([Kahle and Meckes, 2013])
各 xi は内点を持つ凸体 K に値を持つ i.i.d. な一様確率変数とする. limn→∞ nrd
n = ∞ の超臨
界域(super-critical regime)において, K のみに依存した定数 c > 0 が存在して,
E[β1,n] ≤ MWne?cWn
となる. ただし Wn = nrd
n . 特に,
E[β1,n]
n → 0.
Theorem ([Kahle and Meckes, 2013] )
xi は先と同様とする. この時, nrd
n ≥ c log n の連結域(connected regime)の時,
P
Kn が単連結
→ 0 (n → ∞).
? s.t.@simizut22 22](https://image.slidesharecdn.com/16simizut-210923135912/85/16-simizut-22-320.jpg)
![拡張
? 今回扱わなかったが, 古典的なランダムトポロジーの対象として,
Erd?s-Rényi グラフ G(n, p) [Erd?s and Rényi, 1959] がある.
? 今回は 2 次元複体までを考えたが, 一般の次元の複体の一般の次元の Betti
数に対しても同様の結果が得られている.
? 今回はグラフの旗複体に制限して話をしたが, 例えば ?ech 複体がよく扱わ
れている.
? rn を rn(t) という関数として, 確率過程としての極限を考える拡張もなされ
ている.
? Persistent Betti 数への拡張もある.
? さらに, その多変数化への拡張は... あっあっあっ.
? 基本的に, critical は人間が扱うには早すぎる.
? s.t.@simizut22 24](https://image.slidesharecdn.com/16simizut-210923135912/85/16-simizut-24-320.jpg)
ロマ数16 simizut
- 2. 今日の内容 1 グラフと複体 2 ランダム幾何学的複体 3 漸近挙動と相転移 4 まとめ ? s.t.@simizut22 2
- 3. 自己紹介 ? 清水超貴 ? s.t.@simizut22 ? ロマ数過去登壇: #1 : operad #4 : ホモトピー球面のなす群 #9 : Euler 標数と Magnitude #16 : Random Topology ? 群馬県出身 ? 現在: 吉田大学 D ? s.t.@simizut22 3
- 4. 1 グラフと複体 2 ランダム幾何学的複体 3 漸近挙動と相転移 4 まとめ ? s.t.@simizut22 4
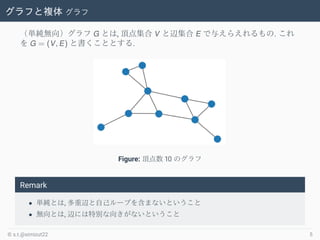
- 5. グラフと複体 グラフ （単純無向）グラフ G とは, 頂点集合 V と辺集合 E で与えらえれるもの. これ を G = (V, E) と書くこととする. Figure: 頂点数 10 のグラフ Remark ? 単純とは, 多重辺と自己ループを含まないということ ? 無向とは, 辺には特別な向きがないということ ? s.t.@simizut22 5
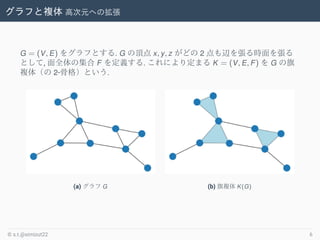
- 6. グラフと複体 高次元への拡張 G = (V, E) をグラフとする. G の頂点 x, y, z がどの 2 点も辺を張る時面を張る として, 面全体の集合 F を定義する. これにより定まる K = (V, E, F) を G の旗 複体（の 2-骨格）という. (a) グラフ G (b) 旗複体 K(G) ? s.t.@simizut22 6
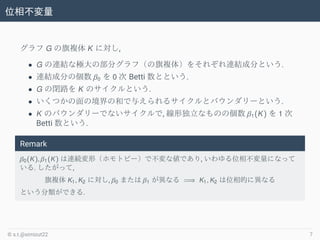
- 7. 位相不変量 グラフ G の旗複体 K に対し, ? G の連結な極大の部分グラフ（の旗複体）をそれぞれ連結成分という. ? 連結成分の個数 β0 を 0 次 Betti 数とという. ? G の閉路を K のサイクルという. ? いくつかの面の境界の和で与えられるサイクルとバウンダリーという. ? K のバウンダリーでないサイクルで, 線形独立なものの個数 β1(K) を 1 次 Betti 数という. Remark β0(K), β1(K) は連続変形（ホモトピー）で不変な値であり, いわゆる位相不変量になって いる. したがって, 旗複体 K1, K2 に対し, β0 または β1 が異なる =? K1, K2 は位相的に異なる という分類ができる. ? s.t.@simizut22 7
- 8. 位相不変量 β0 (a) 連結グラフ β0 = 1 (b) 連結でないグラフ β0 = 2 ? s.t.@simizut22 8
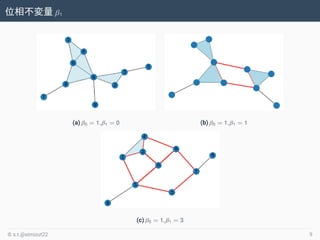
- 9. 位相不変量 β1 (a) β0 = 1, β1 = 0 (b) β0 = 1, β1 = 1 (c) β0 = 1, β1 = 3 ? s.t.@simizut22 9
- 10. 1 グラフと複体 2 ランダム幾何学的複体 3 漸近挙動と相転移 4 まとめ ? s.t.@simizut22 10
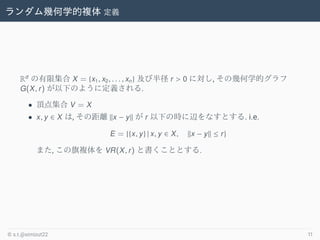
- 11. ランダム幾何学的複体 定義 Rd の有限集合 X = {x1, x2, . . . , xn} 及び半径 r > 0 に対し, その幾何学的グラフ G(X, r) が以下のように定義される. ? 頂点集合 V = X ? x, y ∈ X は, その距離 kx ? yk が r 以下の時に辺をなすとする. i.e. E = {{x, y} | x, y ∈ X, kx ? yk ≤ r} また, この旗複体を VR(X, r) と書くこととする. ? s.t.@simizut22 11
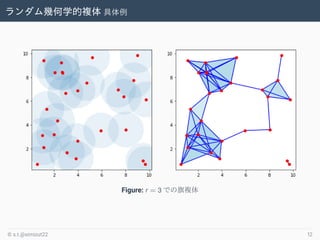
- 12. ランダム幾何学的複体 具体例 Figure: r = 3 での旗複体 ? s.t.@simizut22 12
- 13. ランダム幾何学的複体 具体例 n = 10 として, r = 1 まで発展させると以下のようになる. ? s.t.@simizut22 13
- 14. ランダム幾何学的複体 Betti 数の変化 Figure: [0, 1]4 内の 1000 点から計算した Betti 数の変化 観察 ? β0 は単調減少. b1 は単調ではない. ? β0 ? 1, β1 は r が大きくなると 0 になる. ? s.t.@simizut22 14
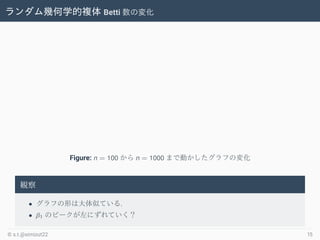
- 15. ランダム幾何学的複体 Betti 数の変化 Figure: n = 100 から n = 1000 まで動かしたグラフの変化 観察 ? グラフの形は大体似ている. ? β1 のピークが左にずれていく？ ? s.t.@simizut22 15
- 16. ランダム幾何学的複体 Betti 数の変化 Q 点の個数 n に応じて, 半径 r = rn も変わったとき, β0(VR(Xn, rn)), β1(VR(Xn, rn)) は n → ∞ でどのような変化をするのか？ ？ A lim n→∞ nrd n = ? ? ? ? ? ? ? ? ? ? ? 0, sub-critical regime, α ∈ (0, ∞), critical regime ∞, super-critical regime のどれになるかに応じて, 挙動が大きく異なる. 相転移現象 ? s.t.@simizut22 16
- 17. 1 グラフと複体 2 ランダム幾何学的複体 3 漸近挙動と相転移 4 まとめ ? s.t.@simizut22 17
- 18. 漸近挙動と相転移 設定 ? x1, x2, . . . , xn, . . . は Rd に値を持つ互いに独立な確率変数列で, 共通の確率密 度関数 f : Rd → R を持つものとする. ? rn を半径の列とする. ? ランダム幾何学的グラフ G(Xn, rn) を Gn , その旗複体 VR(Xn, rn) を VRn と 表す. ? k = 0, 1 として VRn の k 次数 Betti 数 βk (VRn) を βk,n で表す: β0,n = β0(VRn) = β0(Gn), and β1,n = β1(VRn) ? s.t.@simizut22 18
- 19. 漸近挙動と相転移 β0 Theorem ([Penrose et al., 2003]) 1. nrd n → 0 の亞臨界域において, E[β0,n] ≈ n (n → ∞) 2. nrd n → λ ∈ (0, 1) の臨界域において, ? 大数の法則が成立: 0 < c < 1 が存在して, β0,n ≈ cn (n → ∞) ? 中心極限定理が成立: β0,n ? E[β0,n] √ n d ? → N(0, ? σ2 ) 3. nrd n = 2d?1 dωd (c + log n) の時, P(β0,n = 1) → e?e?c ? s.t.@simizut22 19
- 20. 漸近挙動と相転移 亞臨界域 Theorem ([Kahle and Meckes, 2013]) limn→∞ nrd n → 0 の亞臨界域において, 次の極限が存在:（大数の法則） E[β1,n] n4r3d n → C1. Theorem ([Kahle and Meckes, 2013] ) 1. n4 r3d n → 0 の時, P(β1,n = 0) → 1 2. n4 r3d n → α ∈ (0, ∞) の時, β1,n d ? → Poisson(C1α). 3. n4 r3d n → ∞ の時, 次の中心極限定理が成立: β1,n ? E[β1,n] Var(β1,n) d ? → N(0, 1). ? s.t.@simizut22 20
- 21. 漸近挙動と相転移 臨界域 Theorem ([Kahle and Meckes, 2013]) limn→∞ nrd n → c の臨界域(critical regime)において, β1,n ～ n (n → ∞). ? s.t.@simizut22 21
- 22. 漸近挙動と相転移 超臨界域 Theorem ([Kahle and Meckes, 2013]) 各 xi は内点を持つ凸体 K に値を持つ i.i.d. な一様確率変数とする. limn→∞ nrd n = ∞ の超臨 界域(super-critical regime)において, K のみに依存した定数 c > 0 が存在して, E[β1,n] ≤ MWne?cWn となる. ただし Wn = nrd n . 特に, E[β1,n] n → 0. Theorem ([Kahle and Meckes, 2013] ) xi は先と同様とする. この時, nrd n ≥ c log n の連結域(connected regime)の時, P Kn が単連結 → 0 (n → ∞). ? s.t.@simizut22 22
- 23. 1 グラフと複体 2 ランダム幾何学的複体 3 漸近挙動と相転移 4 まとめ ? s.t.@simizut22 23
- 24. 拡張 ? 今回扱わなかったが, 古典的なランダムトポロジーの対象として, Erd?s-Rényi グラフ G(n, p) [Erd?s and Rényi, 1959] がある. ? 今回は 2 次元複体までを考えたが, 一般の次元の複体の一般の次元の Betti 数に対しても同様の結果が得られている. ? 今回はグラフの旗複体に制限して話をしたが, 例えば ?ech 複体がよく扱わ れている. ? rn を rn(t) という関数として, 確率過程としての極限を考える拡張もなされ ている. ? Persistent Betti 数への拡張もある. ? さらに, その多変数化への拡張は... あっあっあっ. ? 基本的に, critical は人間が扱うには早すぎる. ? s.t.@simizut22 24