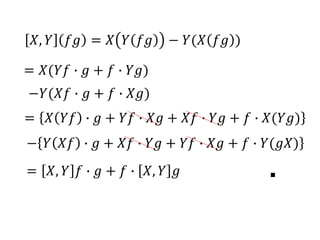More Related Content
What's hot (20)
経験过程経験过程hoxo_m?
Watanabe理論勉強会 第七回 資料
タイトル詐欺で経験过程まで行っておらず、法則収束の説明まで Similar to 情報幾何学の基礎 第2章 4.5 (20)
情报几何学の基础2章补足情报几何学の基础2章补足Hiroki Iida?
教科書とは異なる定義から、等価な接ベクトルを導出しています。普段習う速度ベクトルから導出をしています。
こちらの接空間を参考にしています。
参考ページ:http://www.math.titech.ac.jp/~kawahira/courses/kiso.html
教科書:https://www.amazon.co.jp/dp/4434208810 第10回 配信講義 計算科学技術特論B(2022)第10回 配信講義 計算科学技術特論B(2022)RCCSRENKEI?
本讲义では科学技术计算の一例として、地震分野における大规模有限要素法シミュレーション手法について説明する。ここでは、有限要素法の基础、大规模线形连立方程式の解法の一种である共役勾配法、及び、共役勾配法の并列计算方法について説明する。 More from Tatsuki SHIMIZU (15)
情報幾何学の基礎 第2章 4.5
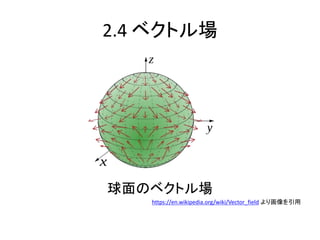
- 5. 2.4 ベクトル場
?; ?1
, … , ? ?
: ?次元多様体?の座標近傍
?
?? ?: 各点?に標準的な接ベクトル
?
?? ?
?
を対応
させる?上のベクトル場
これを用いると,? ∈ ? ? は?上,
? = ? ?
?
?? ?
と局所表示できる(? ?
は当然一意)
- 6. 2.4 ベクトル場
? ? は ?∞
? module の構造を持つ
i.e.
和:
? + ? ? = ? ? + ??
関数倍:
?? ? = ? ? ? ?
- 7. 2.4 ベクトル場
? ∈ ? ? , ? ∈ ?∞
?
?の?への作用 ?? ∈ ?∞
? を次で与える
?? ? = ? ? ?
注意:
関数倍ではない.微積分で行う”方向”微分のようなもの
- 8. 2.4 ベクトル場
?, ? ∈ ? ? に対し,
?, ? ∈ ? ?
が次のようにして定まる.(lie bracket)
?, ? ? = ? ?? ? ? ??
Leibnitz rule を満たすか確認する
- 9. ?, ? ?? = ? ? ?? ? ?(? ?? )
= ?(?? ? ? + ? ? ??)
??(?? ? ? + ? ? ??)
= ? ?? ? ? + ?? ? ?? + ?? ? ?? + ? ? ?(??)
? ? ?? ? ? + ?? ? ?? + ?? ? ?? + ? ? ?(??)
= ?, ? ? ? ? + ? ? ?, ? ? ?
- 10. 2.4 ベクトル場
定義(積分曲線)
? ∈ ? ? に対し,滑らかな曲線 ? = ? ? で
あって,各時刻 ? において
? ? = ? ? ?
の成り立つものを, ?の積分曲線という
remark
常微分方程式の解の存在?一意性定理から,
局所的には存在しかつ一意
- 11. 2.4 ベクトル場
例:?2
? 0 の次のベクトル場を考える
?(?,?) = ??
?2+?2
?
??
+
?
?2+?2
?
??
この,積分曲線は
? = 0
? = 1
?
で与えられる→ 円を描く.
ここで, ?, ? は極座標表示による
- 14. 2.4 ベクトル場
? ∈ ? ? , ? ∈ Ω1
? に対して,
? ? ∈ ?∞
? が,
? ? ? ? ? ?
により定まる
- 15. 2.4 ベクトル場
?; ?1
, … , ? ?
: ?次元多様体?の座標近傍
?? ?
: 各点?に?? ?
?
を対応させる?上の1-form
これを用いると,? ∈ Ω1
? は?上,
? = ?? ?? ?
と局所表示できる
ここで,?? = ?
?
?? ? が成立
)∵ ?
?
?? ? =?? ?? ? ?
?? ? =?? ??
?
= ??
- 17. 2.5 テンソル場
定義
多様体 ? の各点?に対し, ?, ? 型テンソル
?? ?(?,?)
を対応させる対応? = ?? ?∈?
のことを
? 上の ?, ? 型テンソル場という
今まで同様に,局所表示が可能(略)
- 20. 2.5 テンソル場
1. ユークリッド空間 ? ?
:
? = ??,?
2. 2次元球面 ?2
:
? = ??2
+ sin2
? ??2
3. 上半平面
??2
= ??2+??2
?2 = ??? ?
?? ? 2
3. ローレンツ計量
??2
= ??2
? ??2
? ??2
? ??2
Editor's Notes
- #14: テキストとは异なる记号を用いたが,こちらの方が一般的な気がする.
- #20: σコンパクト(加算個のコンパクトの合併)
Σ局所コンパクト:σコンパクトかつ局所コンパクト(各店の近傍でコンパクトが存在)
多様体がσコンパクト→パラコンパクト
パラコンパクトならリーマン計量が存在